Лекции по гидростатике. Определение предмета. Краткие исторические сведения

• Название: Определение предмета. Краткие исторические сведения
• Дата: 22.02.2022
• Размер: 1.47 Mb.
• Имя файла: Лекции по гидростатике.doc
• Тип: Документы; #370303
• страница: 1 из 4

ВВЕДЕНИЕ

ОПРЕДЕЛЕНИЕ ПРЕДМЕТА. КРАТКИЕ ИСТОРИЧЕСКИЕ СВЕДЕНИЯ

Гидравлика - наука, изучающая равновесие и движение жидкости, а также ее взаимодействие с твердыми телами, погруженными в нее, и твердыми поверхностями, граничащими с жидкостью.

Гидравлика позволяет разрабатывать методики решения различных прикладных задач в строительстве, коммунальном хозяйстве, охране водных ресурсов и других сферах человеческой деятельности, связанных с водой и другими жидкостями.

Первым научным трудом в области гидравлики был трактат Архимеда (287—212 гг. до н.э.) «О плавающих телах». Леонардо да Винчи (1452—1519) в XV в. написал работу «О движении и измерении воды», Галилео Галилей (1564—1642) в 1612 г. в своем трактате «Рассуждение о телах, пребывающих в воде, и о тех, которые в ней движутся» рассмотрел условия равновесия жидкости, обосновал основные законы плавания тел. Далее Эванджелиста Торричелли (1608—1647) предложил в 1643 г. формулу для определения скорости истечения жидкости из отверстия, Блез Паскаль (1623—1662) открыл закон о передаче внешнего давления в жидкости, который до настоящего времени служит основанием для конструирования гидравлических машин (прессы, домкраты, тормоза и др.), Исаак Ньютон (1643—1727) в 1686 г. предложил гипотезу о законе внутреннего трения в движущейся жидкости.

Однако формирование гидравлики как науки, базирующейся на математических уравнениях, дифференциальных и интегральных исчислениях, произошло в XVIII в. и стало возможным благодаря работам академиков Петербургской Академии наук: Леонарда Эйлера (1707-1783), Даниила Бернулли (1700-1782), Михаила Васильевича Ломоносова (1711-1765).

Даниил Бернулли в 1738 г. дал теоретическую основу уравнения, отражающего закон сохранения энергии для жидкости, справедливо считающегося основополагающим в практических расчетах по гидравлике. Леонард Эйлер в 1755 г. вывел дифференциальные уравнения равновесия и движения жидкости. М.В. Ломоносов открыл и обосновал законы сохранения массы вещества и энергии.

Кроме российских ученых огромный вклад в развитие гидравлики внесли западно-европейские ученые. Антуан Шези (1718— 1798) изучал равномерное движение жидкости, Джованни Батиста Вентури (1746—1822) исследовал истечение жидкости через отверстия и посадки, Юлиус Вейсбах (1806—1871) занимался изучением сопротивления движения жидкости. Осборн Рейнольдс (1892—1912) много труда положил в изучение ламинарного и турбулентного движений.

В России во второй половине XIX и начале XX в. наиболее известны работы Ипполита Степановича Громеки (1851 — 1889), Николая Павловича Петрова (1836-1920), Николая Егоровича Жуковского (1847-1921) по винтовым потокам, теории смазки, гидравлическому удару. На Западе к наиболее известным работам в начале XX в. следует отнести полуэмпирическую теорию турбулентного течения Людвига Прандтля (1875-1953).

Развитие гидротехнического, гидромелиоративного строительства в СССР позволило создать советскую гидравлическую школу. Можно назвать много известных имен, благодаря которым гидравлическая наука обогатилась глубокими исследованиями и теоретическими разработками в различных областях гидравлики. В первую очередь к ним следует отнести Николая Николаевича Павловского, И.И. Агроскина, Евгения Александровича Замарина, Михаила Дмитриевича Чертоусова, Pомана Pомановича Чугаева, И.И. Леви, П.Г. Киселева, Л.С. Животовского, А.Д. Альтшуля и др.

В последние десятилетия развитие гидравлики неразрывно связано с применениями ЭВМ. Широко используются численные методы гидравлических расчетов, а также численное моделирование гидравлических явлений.
Глава 1. ЖИДКОСТИ И ИХ ОСНОВНЫЕ ФИЗИЧЕСКИЕ СВОЙСТВА

Жидкости. В природе различают четыре вида состояния вещества: твердое, жидкое, газообразное и плазменное. Основное отличие жидкостей от твердых тел заключается в их текучести, т.е. способности легко принимать форму сосуда, в который жидкость поместили, при этом объем жидкости не изменяется. Газ тоже обладает текучестью, но при этом занимает любой предоставленный ему объем. В сосудах жидкость образует свободную поверхность, а газ аналогичной поверхностью не обладает. Однако с точки зрения механики и жидкость, и газ подчиняются одним и тем же закономерностям в случае, если сжимаемостью газа можно пренебречь. Поэтому в гидравлике под термином «жидкость» понимаются и собственно жидкости (которые часто называют капельными жидкостями), и газы (газообразные жидкости).

Основные свойства жидкости (при рассмотрении задач механики жидкости) - это плотность, способность изменять свой объем при нагревании (охлаждении) и изменениях давления, вязкость жидкости. Рассмотрим каждое из свойств жидкости подробнее.

Плотность жидкости. Плотностью жидкости называется ее масса, заключенная в единице объема:

(1.1)

где - масса жидкости; - объем жидкости.

Единица измерения плотности - кг/м³.

Так как вода является наиболее распространенной в природе жидкостью, в качестве примера количественного значения параметра, определяющего то или иное свойство жидкости, будем приводить значение рассматриваемого параметра для воды. Плотность воды при 4°С кг/м³. Плотность жидкости уменьшается при увеличении температуры. Однако для воды эта закономерность справедлива только с 4 °С, в чем проявляется одно из аномальных свойств воды.

Удельный вес. Удельный вес - это вес жидкости, приходящийся на единицу объема:

(1.2)

где - вес жидкости в объеме .

Единица измерения удельного веса - Н/м³. Удельный вес воды при температуре 4°С Н/м³.

Плотность и удельный вес связаны между собой соотношением

(1.3)

где - ускорение свободного падения.

Температурное расширение. Это свойство жидкости характеризуется изменением объема при изменении температуры, которое определяется температурным коэффициентом объемного расширения жидкости :

(1.4)

где - начальный объем жидкости при начальной температуре; - изменение объема после уменьшения или увеличения температуры; - изменение температуры.

Единица измерения - град^-1, для воды при °С 1/°С.

Сжимаемость. Это свойство жидкости менять свой объем при изменении давления, которое характеризуется коэффициентом объемного сжатия :

(1.5)

где - начальный объем жидкости; -изменение объема после изменения давления; - изменение давления.

Единица измерения - Па^-1.

Коэффициент объемного сжатия капельных жидкостей мало меняется в зависимости от давления и температуры. Для воды Па^-1.

Величина, обратная коэффициенту объемного сжатия, называется модулем упругости жидкости и определяется по формуле

(1.6)

Для воды Па.

Вязкость жидкости - свойство жидкостей оказывать сопротивление сдвигу. Это свойство проявляется только при движении жидкостей. Вязкость характеризует степень текучести жидкости. Наряду с легко подвижными жидкостями (вода, спирт, воздух и др.) существуют очень вязкие жидкости (глицерин, машинные масла и др.).

Вязкость жидкости характеризуется динамической вязкостью .

И. Ньютон выдвинул гипотезу о силе трения F, возникающей между двумя слоями жидкости на поверхности их раздела площадью , согласно которой сила внутреннего трения в жидкости не зависит от давления, прямо пропорциональна площади соприкосновения слоев и быстроте изменения скорости в направлении, перпендикулярном направлению движения слоев, и зависит от рода жидкости.

Пусть жидкость течет по плоскому дну параллельными ему слоями (рис. 1.1).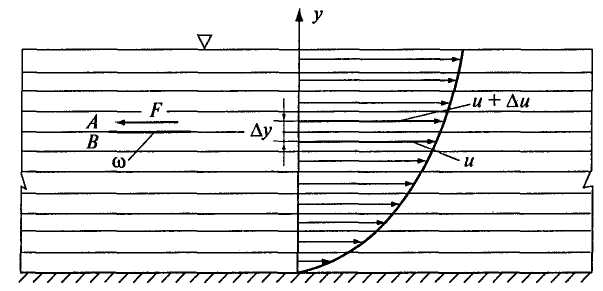



Рис.1.1

Вследствие тормозящего влияния дна слои жидкости будут двигаться с разными скоростями. На рис. 1.1 скорости слоев показаны стрелками. Рассмотрим два слоя жидкости, середины которых расположены на расстоянии друг от друга. Слой А движется со скоростью , а слой В - со скоростью .

На площадке вследствие вязкости возникает сила сопротивления F. Согласно гипотезе Ньютона эта сила

(1.7)

коэффициент пропорциональности в этой формуле и является динамической вязкостью, отношение называется градиентом скорости.

Таким образом, динамическая вязкость является силой трения, приходящейся на единицу площади соприкосновения слоев жидкости при градиенте скорости, равном единице. Размерность - Па с.

Гипотеза И. Ньютона, представленная в формуле (1.7), экспериментально подтверждена и математически оформлена в дифференциальном виде

(1.8)

основоположником гидравлической теории смазки Н.П. Петровым и в настоящее время носит название закона внутреннего трения Ньютона.

В гидравлических расчетах часто удобнее пользоваться другой величиной, характеризующей вязкость жидкости, - :

(1.9)

Эта величина называется кинематической вязкостью. Размерность - м²/с.

Название «кинематическая вязкость» не несет особого физического смысла, так как название было предложено потому, что размерность похожа на размерность скорости.

Вязкость жидкости зависит как от температуры, так и от давления. Кинематическая вязкость капельных жидкостей уменьшается с увеличением температуры, а вот вязкость газов, наоборот, возрастает с увеличением температуры. Кинематическая вязкость жидкостей при давлениях, встречающихся в большинстве случаев на практике, мало зависит от давления, а вязкость газов с возрастанием давления уменьшается.

Вязкость жидкости измеряют с помощью вискозиметров различных конструкций.

Жидкости, для которых справедлив закон внутреннего трения Ньютона (1.8), называют ньютоновскими. Существуют жидкости, которые не подчиняются закономерности (1.8), к ним относятся растворы полимеров, гидросмеси из цемента, глины, мела и др. Такие жидкости относятся к неньютоновским.

Пример 1.1

Определите массу бензина, заполняющего цилиндрический резервуар диаметром м и высотой м при температуре 20°С ( кг/м³).

Ответ: 204,9кг.

Пример 1.2

Определите количественные изменения давления в воде, находящейся в герметически замкнутом резурвуаре, при изменении температуры от 10 до 20°С, если считать материал резервуара абсолютно жестким.

Если бы резервуар не был закрыт герметически, изменение объема можно было бы найти из формулы (1.4) . Тогда новый объем , но объем неизменен. Значит, должно измениться внешнее давление на поверхности воды, а значит, и давление в каждой ее точке не величину , которую определим из формулы (1.5):







°С, 1/°С,

°С, Па^-1,

Тогда

Па.

Глава 2. ГИДРОСТАТИКА

2.1 РАВНОВЕСИЕ ЖИДКОСТИ И ДЕЙСТВУЮЩИЕ СИЛЫ

Гидростатика - раздел гидравлики, в котором изучается жидкость, находящаяся в покое.

Если на выделенную массу жидкости не действуют внешние силы, то все частицы этой массы остаются неподвижными относительно выбранной системы координат, т.е. находятся в покое или движутся прямолинейно с одинаковой для всех частиц скоростью, при этом взаиморасположение частиц остается постоянным. Такое состояние жидкости называется равновесным. В случае воздействия внешних сил равновесное состояние жидкости либо сохраняется, либо жидкость переходит в состояние движения.

Рассмотрим, какие силы могут действовать на жидкость, находящуюся в равновесии, и каким условиям должны удовлетворять внешние силы, чтобы условия равновесия жидкости не нарушались.

Выделим некоторый объем Wиз массы жидкости, находящейся в резервуаре, и рассмотрим силы, действующие на этот объем.

Эти силы могут быть поверхностными и массовыми.

Поверхностные силы - это силы давления, действующие на поверхности выделенного объема, они пропорциональны размеру площади , взятой на этой поверхности (силы _{, ,…,} ) (рис. 2.1).

Массовые силы - это внешние силы, пропорциональные массе жидкости, заключенной в выделенном объеме (сила Rна рис. 2.1). К таким силам относятся силы тяжести и силы инерции.

Для того чтобы жидкость находилась в состоянии равновесия (покоя), необходимо, чтобы силы, действующие в точках ее граничной поверхности, были направлены под углом 90° к этой поверхности. Действительно, так как жидкости сопротивляются сжимающим усилиям и в силу свойства текучести не могут сопротивляться сдвигающим усилиям, сила N (рис. 2.2) должна быть направлена нормально (под углом 90°) к поверхности, ограничивающей объем жидкости, и не может быть направлена под другим углом, как, например, сила F, стремящаяся сдвинуть частицу жидкости, находящуюся в точке М. (Силу Fможно разложить на две составляющие - N и Т.)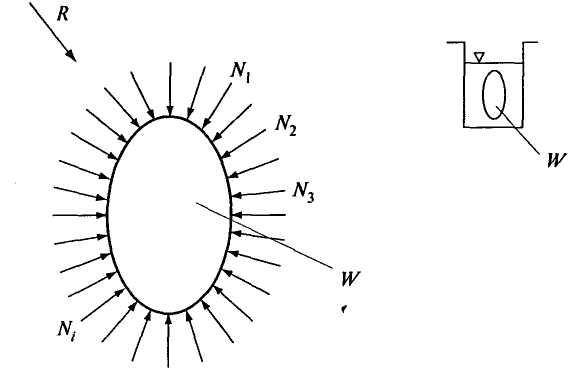



Рис. 2.1. Силы, действующие на жидкость в условиях равновесия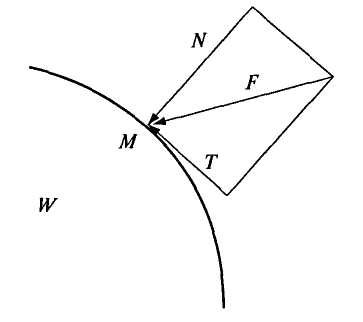



Рис. 2.2. Действие поверхностных сил

В то же время сила N не может быть направлена от поверхности, так как жидкости не сопротивляются растягивающим усилиям.