Расширение понятия числа. лекции Расширение понятия числа (1). Расширениепонятияо

• Название: Расширениепонятияо
• Анкор: Расширение понятия числа
• Дата: 31.01.2022
• Размер: 64.65 Kb.
• Имя файла: лекции Расширение понятия числа (1).docx
• Тип: Документы; #347190
• страница: 1 из 9

^{РАСШИРЕНИЕ}ПОНЯТИЯОЧИСЛЕ

1. 
   Краткие исторические сведения о возникновении понятия дроби и отрицательного числа
   

Большинство применений математики связано с измерением величин, но для этих целей натуральных чисел недостаточно: не всегда единица величины укладывается целое число раз в измеряемой величине. Чтобы в такой ситуа- ции точно выразить результат измерения, нужно расширить запас чисел, введя числа, отличные от натуральных. К этому выводу люди пришли еще в глубо- кой древности. Измерение длин, площадей, масс и других величин привело сначала к возникновению дробных чисел – получили рациональные числа, а в 5 в до н. э. Пифагором было установлено, что существуют отрезки, длину ко- торых нельзя выразить рациональным числом. Позднее, в связи с решением этой проблемы появились иррациональные числа. Рациональные и иррацио- нальные числа назвали действительными.

Строгое определение действительного числа и обоснование его свойств было дано в 19 веке.

Взаимосвязи между различными множествами чисел можно изобразить наглядно при помощи кругов Эйлера.
N – натуральные

Z - целые

Q - рациональные

R – действительные
Действительные числа – не последние в ряду различных чисел. Процесс, начавшийся с расширения множества натуральных чисел, продолжается и се- годня – этого требует развитее различных наук и самой математики.

Знакомство учащихся с дробными числами происходит в начальных классах, а в средней школе понятие дроби уточняется и расширяется.

Целыечисла

2. Понятие об отрицательном числе

Практическая деятельность и потребности самой математики приводит к необходимости расширения множества натуральных чисел и обогащению са- мого понятия числа. Многие величины допускают двойное смысловое истол- кование, и поэтому числовое значение такой величины без дополнительных

указаний определяет ее неоднозначно. Например, температура воздуха 1 не определяет нагретость воздуха без указания холода или тепла; информация

«магазин находится на этой улице в 500 м от перекрестка» не определяет ме- стонахождения магазина, так как не указано, в какую сторону от перекрестка надо двигаться к магазину: направо или налево.

Из этих примеров видно, что целесообразно наряду с натуральными чис- лами иметь запас других чисел, которые описывали бы не только величину, но и «направление» и применение которых освободило бы от дополнительных пояснений. Такие числа введены в науку и их принято обозначать как нату- ральные числа, но со знаком « – » – они называются отрицательными.

Натуральные числа, число 0 и целые отрицательные числа образуют множество целых чисел, которые обозначаются Z.

Возьмем прямую и отметим на ней произвольную точку 0. Возьмём про- извольную точку Е, например, справа от 0. Условимся, что числу 1 соответ- ствует точка Е.

О Е




Отложим от точки Е справа отрезок, равный ОЕ (соответственно число 2). Этот процесс откладывания отрезков можно продолжать неограниченно. При этом каждому натуральному числу n будет соответствовать точка на пря- мой.

Назовем прямую ОЕ координатной прямой, число n, соответствующее точке М, координатой точки М и условимся обозначать М(n).

Установим теперь взаимнооднозначное соответствие между множеством отрицательных чисел N и некоторым множеством точек координатной прямой ОЕ, находящихся слева от точки О. Для этого будем откладывать отрезки, равные отрезку ОЕ, слева от точки О. Таким образом, мы получим точки, со- ответствующие числам –1, –2, –3, ….

Теперь уже всем числам из множества Z соответствуют точки на коорди- натной прямой. Числа 1 и –1 называются противоположными. Противопо- ложные числа изображаются точками, симметричными относительно начала координат на числовой прямой. Противоположность двух чисел – свойство взаимное: если число –n противоположно числу n, то число, противоположное числу –n, есть число –(–n )= n.

Рассмотрим два противоположных числа, например, –5 и 5. Точки, изоб- ражающие эти числа, находятся на одинаковом расстоянии в пять единиц от точки О, но с разных сторон от неё. Число «5» называют абсолютным значе- нием (модулем) числа –5 и числа 5.

Абсолютным значением (модулем) целого числа n называется расстояние от начала координат до точки, соответствующей этому числу. Модуль числа nобозначаются n.

Определение. Модулемчисла zZ называется само это число, если оно неотрицательное, и противоположное ему число –z, если оно отрицательно, т. е.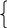

Z, если Z > 0

Z = – Z, если Z < 0

Определение. Число а меньше числа b, если b=а+k.

Геометрическая интерпретация отношения «меньше» такова: a < b тогда и только тогда, когда точка А(а) находится левее точки В(b) на координатной прямой.

Правило сложения целых чисел: сумма двух целых чисел одинакового знака есть число того же знака, модуль которого равен сумме модулей слагае- мых. Сумма двух чисел разных знаков есть число, знак которого совпадает со знаком слагаемого, имеющего больший модуль, а его модуль равен разности между большим и меньшим модулем.

Например, –7 + 5 = –(–7– 5) = –(7–5) = –2.

Теорема. Сложение в Z коммуникативно, ассоциативно и монотонно.

Определение. Вычитание в Z – это сложение с противоположным чис- лом, т.е. a – b= a +(–b).

Вычитание в Z – всегда выполнимая операция.

Определение. Произведение двух целых чисел есть положительное чис- ло, если оба сомножителя имеют одинаковые знаки, и отрицательное число, если знаки сомножителей разные. Модуль произведения равен произведению модулей сомножителей.

Определение. Деление целых чисел определяется как действие, обрат- ное умножению: частным от деления одного числа (делимого) на другое чис- ло (делитель) называется третье число, произведение которого на делитель дает делимое, т.е. m : n = k, что означает kn = m.

Деление нуля на любое целое n0 дает нуль.

Правило деления целых чисел: модуль частного от деления целых чисел равен частному от деления модуля делимого на модуль делителя, знак част- ного положителен, если делимое и делитель одинакового знака, и отрицате- лен, если делимое и делитель разных знаков.