Расширение понятия числа. лекции Расширение понятия числа (1). Расширениепонятияо

• Название: Расширениепонятияо
• Анкор: Расширение понятия числа
• Дата: 31.01.2022
• Размер: 64.65 Kb.
• Имя файла: лекции Расширение понятия числа (1).docx
• Тип: Документы; #347190
• страница: 7 из 9

Сравнение десятичных дробей и действия над ними. Процент

Сравнение десятичных дробей и арифметические действия над ними легко выполнить, если дроби имеют один и тот же знаменатель.

В основе привидения десятичных дробей к общему знаменателю лежит

следующее утверждение: есликдесятичнойдроби


A, а_n1...a₀

приписатьспра-

валюбоечислонулей,тополучитсядесятичнаядробь,равнаяданной.

Это свойство позволяет приводить десятичные дроби к общему знаме- нателю следующим образом: если у одной дроби после запятой стоит пцифр, а у другой р цифр, причем п р, то для привидения их к общему знаме-нателюдостаточно кпервойдробиприписатьсправа р–п нулей.

Пользуясь этим правилом, легко выполнять сравнение десятичных дробей, так как оно сводится к сравнению натуральных чисел: чтобы срав-нить две десятичные дроби, надо уравнять в них число десятичных знаковпосле запятой, отбросить запятые и сравнить получившиеся натуральныечисла.

Например, 4,62517 4,623, так как 462517 462300.

Для дробей, имеющих одинаковые знаменатели, сложение и вычитание сводится к соответствующим операциям над их числителями. Это позволяет свести сложение и вычитание десятичных дробей к действиям над натураль- ными числами.

Например, 2,54+3,7126= 2,5400+3,7126= ²⁵⁴⁰⁰ + ³⁷¹²⁶ = ⁶²⁵²⁶ =

6,2526.

10000

10000

10000

Умножение и деление десятичных дробей не требует приведения их к общему знаменателю, но они также сводятся к соответствующим действиям над натуральными числами.

Среди десятичных дробей выделяют и часто используют дробь 0,01. Ее

называют процентом и обозначают 1%. Запись р% обозначает

^р. Напри-

100

мер, 25% – это дробь

²⁵ или 0,25.

100

Проценты были введены, когда не существовало десятичных дробей. Чтобы произвести расчеты по займам, определяли прирост капитала из рас- чета 100 денежных единиц. Этот прирост и называли числом процентов (pro centum – на сто).

11. Бесконечные десятичные дроби

Простота сравнения и выполнения действий над десятичными дробями

приводит к следующему вопросу: любую ли дробь вида

^m(m,nN) можно

n

записать в виде конечной десятичной дроби, т.е. дроби, у которой после за- пятой стоит конечное число цифр? Ответ на этот вопрос дает теорема.

Теорема. Для того чтобы несократимая дробь

^mбыла равна десятичной,

n

необходимо и достаточно, чтобы в разложение ее знаменателя n на простые множители входили лишь простые числа 2 и 5.

Например,

²³ можно записать в виде десятичной дроби, так как она не-

80

сократима и 80 = 2⁴  5. Дробь

¹¹ несократимая, но 15 = 3  5. Поскольку в

15

разложение знаменателя входит множитель, отличный от 2 и 5, то эту дробь нельзя записать в виде десятичной.

Дробь

¹ нельзя представить в виде конечной десятичной дроби. Но деля

3

1 на 3, получаем 0,3  ¹  0,4. Далее находим, что 0,33  ¹  0,34 и т.д.

3 3

Вообще для любого nимеем: 0,33…3  ¹  0,33…4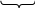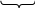

3

пцифр n цифр

Вместо того чтобы писать бесконечное множество неравенств, говорят,

что дроби

¹ соответствует бесконечнаядесятичнаядробь0,33..3… Это

3

означает, что если отбросить в бесконечной дроби все цифры, начиная с не-

которой, то будем иметь число, меньшее

¹ , а если в полученном числе уве-

3

личить последнюю цифру на 1, то будет число, большее ¹ .

3

Любую конечную десятичную дробь можно записать в виде бесконеч- ной, приписав к ней справа последовательность нулей. Например, 0,25 = 0,2500…0…

Бесконечные десятичные дроби, которые получаются при записи по- ложительного рационального числа, обладают одной особенностью – они яв- ляются периодическими. Это значит, что, начиная с некоторой цифры, они образуются бесконечным повторением одной и той же группы цифр. Напри-

мер, число

³ выражается бесконечной десятичной дробью 0,2727…27…,

11

число

⁸ – бесконечной десятичной дробью 0,14545..45… Для краткости

55

первую из дробей пишут в виде 0,(27), а вторую – в виде 0,1(45). В скобки за- ключают повторяющуюся группу цифр, которая называется периодом этой дроби. Вместо 0,(27) можно написать 0,2(72), но эта запись более длинная.

Если в разложение знаменателя несократимой дроби на простые мно- жители не входят цифры 2 и 5, то при обращении этой дроби в бесконечную десятичную дробь получится чистая периодическая дробь, т.е. дробь, период которой начинается сразу после запятой. Например, 0,(27). Если же в разло- жение знаменателя входит множитель 2 или 5, то периодическая дробь ока- зывается смешанной (например, 0,1(45)) – дробь, у которой между запятой и началом периода будет несколько цифр (а именно столько, каков больший из показателей степеней множителей 2 и 5). Например, если п=2³ 5² 711, то между запятой и началом периода окажутся три цифры.

Теорема. Любое положительное рациональное число представимо бес- конечной периодической десятичной дробью.

Доказательство.Пусть рациональное число представлено несократимой

дробью

^m. Чтобы преобразовать ее в десятичную, надо выполнить деление

n

натурального числа m на натуральное число n. При этом будут остатки, меньшие n, т.е. числа вида 0,1,2…n–1. Если хотя бы один из остатков ока- жется равным нулю, то после деления получится конечная десятичная дробь (или, что то же самое, бесконечная десятичная дробь, заканчивающаяся по- следовательностью нулей). Если же все остатки отличны от нуля, то деление будет представлять собой бесконечный процесс, но количество различных остатков конечно, и поэтому, начиная с некоторого шага, какой-то остаток повторится, что приведет к повторению цифр в частном.