Расширение понятия числа. лекции Расширение понятия числа (1). Расширениепонятияо
 Скачать 64.65 Kb. Скачать 64.65 Kb.
|
Множество положительных действительных чисел и действия над ними. СвойстваОбъединение двух множеств чисел: положительных рациональных и по- ложительных иррациональных называется множеством положительных дей- ствительных чисел и обозначается символом R+.  Таким образом, Q+ J+=R+. Таким образом, Q+ J+=R+.R+ Любое положительное действительное число может быть представлено бесконечной десятичной дробью – периодической (если оно является рацио- нальным), либо непериодической (если оно является иррациональным). Для любого действительного числа асправедливо неравенство: аk а а’k.  Например, десятичным приближением числа =1,73205… по недостат- Например, десятичным приближением числа =1,73205… по недостат-ку с точностью до 0,001 является число 1,732, а по избытку – число 1,733. Видим, что десятичные приближения действительного числа являются конечными десятичными дробями. На этом и основываются, определяя дей- ствия над ними. Пусть даны действительные числа а и b, аkи bk– их приближенные зна- чения по недостатку, а’kи bk’– приближенные значения по избытку. Определение. Суммой положительных действительных чисел а и bназывается такое число а+ b, которое удовлетворяет следующему неравен- ству: аk+bk а+b а’k+bk’. 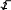 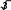 Например, найдем сумму + с точностью до 0,001. Возьмем деся- Например, найдем сумму + с точностью до 0,001. Возьмем деся-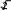 тичные приближения данных чисел с точностью до 0,0001 тичные приближения данных чисел с точностью до 0,00011,4142 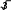 1,7320 1,7320 1,4143 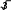 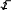 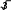 1,7321. 1,7321.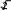 Тогда 3,1462 3,146. Тогда 3,1462 3,146.+ 3,1464. С точностью до 0,001 сумма + равна 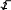 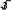 Определение. Произведением положительных действительных чисел аи b называется такое число а b, которое удовлетворяет следующим услови- ям: аk bk а b а’k bk’. Определение. Произведением положительных действительных чисел аи b называется такое число а b, которое удовлетворяет следующим услови- ям: аk bk а b а’k bk’.Например, найдем произведение с точностью до 0,1. Возьмем де- 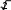 сятичные приближения данных чисел с точностью до 0,01 сятичные приближения данных чисел с точностью до 0,011,41 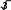 1,73 1,73 1,42 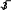 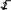 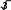 1,74. 1,74.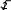 Тогда 2,4393 2,4. Тогда 2,4393 2,4. 2,4708. С точностью до 0,1 произведение равно Сложение и умножение положительных действительных чисел обладает свойствами коммутативности и ассоциативности, а умножение дистрибутив- но относительно сложения и вычитания. Таким образом, для любых положи- тельных действительных чисел выполняются следующие равенства: a+ b=b+ a, 2)a+ (b+c)=(a+ b)+c, 3)a b=b a, 4)(a b) c =a (b c), a (b c)=ab ac. Свойства множества положительных действительных чисел:МножествоR+являетсяупорядоченныммножеством. Так как отношение «меньше» для положительных действительных чисел транзитивно и антисимметрично, то оно является отношением порядка, а множество R+ – упорядоченным множеством. Вмножестве R+нетнинаименьшего,ни наибольшегоэлемента. Кроме того, между любыми двумя числами из R+ лежит бесконечно много рациональных чисел. Непрерывность: если числовое множество Х расположено слева отчислового множества Y, то найдется хотя бы одно число, разделяющее этимножества.Например, удалим из множества R+ число 6. Обозначим через Х множество чисел, меньших 6, а через Y – чисел, больших 6. Хотя Х располо- жено слева от Y, после удаления числа 6 нет ни одного числа, разделяющего эти множества. Значит, смысл свойства непрерывности состоит в том, что в множестве R+ нет не только таких «скачков», как, например, в множестве N натуральных чисел, но и таких «щелей», как в множестве Q+ положительных рациональных чисел. 15. Множество действительных чисел и действия над нимиC помощью положительных действительных чисел можно выразить ре- зультат измерения любой скалярной величины: длины, площади, массы и т.д. Но на практике часто нужно выразить числом не результат измерения вели- чины, а её изменение. Причем её изменение может происходить различно – она может увеличиваться, уменьшаться или оставаться неизменной. Поэтому, чтобы выразить изменение величины, кроме положительных действительных чисел нужны иные числа, а для этого нужно расширить множество R+, при- соединив к нему число 0 и отрицательные числа. Объединение множестваположительных действительных чисел смножеством отрицательных действительных чисел и нулем есть множе-ство Rвсех действительных чисел. Множество R действительных чисел и множество точек координатной прямой находятся во взаимно однозначном соответствии: каждому действи- тельному числу соответствует единственная точка координатной прямой и каждая точка координатной прямой соответствует единственному действи- тельному числу. Действительные числа сравнивают, определяя отношения «меньше» и «больше» так: a <b, если оно расположено левее на координатной прямой; а b,если оно расположено правее на координатной прямой. Из этого определения вытекает, что любое положительное число больше нуля, а любое отрицательное число меньше нуля. Кроме того, по определе- нию «меньше» и «больше» можно получить утверждение: aтогда и только тогда, когда разность a–b есть отрицательное число; a>b тогда и только то- гда, когда разность a–b есть положительное число. Для любых заданных действительных чисел a и b истинно только одно из положений: a Действия над действительными числами выполняются по следующим правилам. Суммой двух действительных чисел называется число, которое удовле- творяет условиям: сумма двух положительных чисел есть число положительное и нахо- дится по правилам, определённым во множестве положительных дей- ствительных чисел. сумма двух отрицательных чисел есть число отрицательное; чтобы найти модуль суммы, надо сложить модули слагаемых; сумма двух чисел, имеющих разные знаки, есть число, которое имеет тот же знак, что и слагаемое с большим модулем; чтобы найти модуль суммы, надо из большего модуля вычесть меньший. Произведением двух действительных чисел называется число, которое удовлетворяет условиям: произведение двух положительных чисел есть число положительное и находится по правилам, определённым во множестве положительных действительных чисел; произведение двух отрицательных чисел есть число положительное; произведение двух чисел, имеющих разные знаки, есть число отрица- тельное; чтобы найти модуль произведения, надо перемножить модули этих чисел. Вычитание и деление действительных чисел определяются как действия, обратные соответственно сложению и умножению. Вычитание во множестве действительных чисел выполняется всегда, так же как и деление, за исклю- чением случая деления на нуль. |
