программирования ответ. Решение (11 4 3) 3 6
 Скачать 50.17 Kb. Скачать 50.17 Kb.
|
|
Вариант 2 Даны два положительных действительных числа. Найти среднее арифметическое и среднее геометрическое этих чисел. Среднее геометрическое вычисляется по формуле: 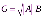 Допустим, имеется ряд чисел: 11, 4, и 3. Средним арифметическим называется сумма всех чисел, поделенная на количество данных чисел. То есть в случае чисел 11, 4, 3, ответ будет 6. Как образом получается 6? Решение: (11 + 4 + 3) / 3 = 6 В знаменателе должно стоять число, равное количеству чисел, среднее которых нужно найти. Сумма делится на 3, так как слагаемых три. Теперь надо разобраться со средним геометрическим. Допустим, есть ряд чисел: 4, 2 и 8. Средним геометрическим чисел называется произведение всех данных чисел, находящееся под корнем со степенью, равной количеству данных чисел.То есть в случае чисел 4, 2 и 8 ответом будет 4. Вот каким образом это получилось: Решение: ∛(4 × 2 × 8) = 4 В обоих вариантах получились целые ответы, так как для примера были взяты специальные числа. Так происходит отнюдь не всегда. В большинстве случаев ответ приходится округлять или оставлять под корнем. Например, для чисел 11, 7 и 20 среднее арифметическое ≈ 12,67, а среднее геометрическое - ∛1540. А для чисел 6 и 5 ответы, соответственно, будут 5,5 и √30. Если имеется ряд чисел, состоящий только либо из единиц, либо из нулей. Примечательно также то, что ответ не зависит от их количества. Доказательство с единицами: (1 + 1 + 1) / 3 = 3 / 3 = 1 (среднее арифметическое). ∛(1 × 1 × 1) = ∛1 = 1(среднее геометрическое). Доказательство с нулями: (0 + 0) / 2=0 (среднее арифметическое). √(0 × 0) = 0 (среднее геометрическое). 2. Среднее арифметическое нескольких чисел — это сумма данных чисел, делённая на их количество. Так, например: — среднее арифметическое чисел a и b равно 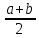 ; ; — среднее арифметическое чисел a, b и c равно 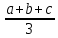 ; ;— среднее арифметическое чисел a, b, c и d равно 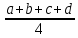 . .— среднее арифметическое чисел a1, a2, . . . , an равно 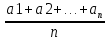 Среднее арифметическое можно вычислять для чисел любого знака. Однако далее, если нет специальных оговорок, мы считаем все рассматриваемые числа неотрицательными. — среднее геометрическое чисел a и b равно 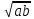 ; ;— среднее геометрическое чисел a, b и c равно 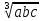 — среднее геометрическое чисел a, b, c и d равно 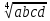 . .— среднее геометрическое чисел a1, a2, . . . , an равно 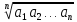 . . |
