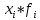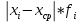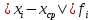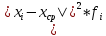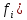Практическая работа по статистике. Задачи по показателям вариации
 Скачать 48.87 Kb. Скачать 48.87 Kb.
|
|
ЗАДАЧИ ПО ПОКАЗАТЕЛЯМ ВАРИАЦИИ Имеется ряд чисел: 0,4; 3,9; 1,5; 5,1; 2,6; 6,8; 1,2; 2,1; 3,3; 3,2; 5,9; 4,7; 4,5; 2,9; 3,4; 4,7; 3,8; 0,3. Определить размах вариации, среднюю арифметическую величину, среднее линейное отклонение, дисперсию, среднеквадратическое отклонение, коэффициент осцилляции, линейный коэффициент вариации, коэффициент вариации. Сделать выводы.
Размах вариации: R = xmax – xmin R = 6,8-0,3=6,5 Среднюю арифметическую величину: 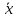 = =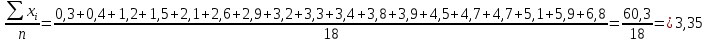 Среднее линейное отклонение: 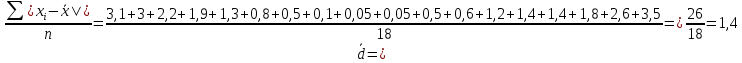 Дисперсия: 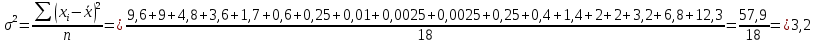 Среднеквадратическое отклонение: 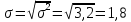 Коэффициент осцилляции: 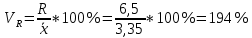 Линейный коэффициент вариации: 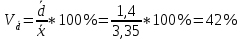 Коэффициент вариации: 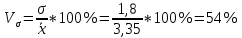 Вывод: коэффициент вариации равен 54%, значит, совокупность по своему составу не однородна, так как V>33%. Распределение числа слов в телеграмме в двух почтовых отделениях характеризуется следующими данными:
Определить для каждого почтового отделения: а) среднее число слов в одной телеграмме; б) среднее линейное отклонение; в) линейный коэффициент вариации. А) Среднее число слов в одной телеграмме для отделения А: 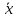 = =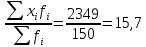 Среднее число слов в одной телеграмме для отделения Б: 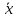 = =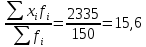 Б) Среднее линейное отклонение для отделения А: 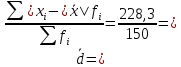 1,5 1,5Среднее линейное отклонение для отделения Б: 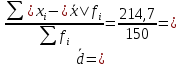 1,4 1,4В) Линейный коэффициент вариации для отделения А: 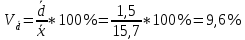 Линейный коэффициент вариации для отделения Б: 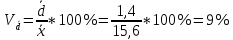 Распределение длины пробега фуры торговой компании характеризуется следующими данными:
Определить: а) среднюю длину пробега за один рейс; б) среднее квадратическое отклонение; в) коэффициент вариации. Оценить количественную однородность совокупности. А) Определим среднюю длину пробега за один рейс: 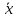 = =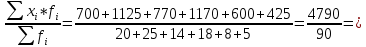 53,2 53,2 среднее квадратическое отклонение: среднее квадратическое отклонение: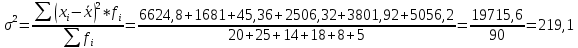 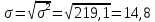 В) 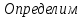 коэффициент вариации: коэффициент вариации: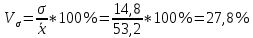 Вывод: коэффициент вариации равен 27,8%, значит, совокупность по своему составу является количественно однородной, так как 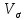 < 33%. < 33%.Имеются следующие данные о балансовой прибыли предприятий за два квартала:
Определить: а) среднюю из внутригрупповых, межгрупповую и общую дисперсию балансовой прибыли предприятия; б) коэффициент детерминации и эмпирическое корреляционное отношение. Сделать выводы. А) Средние величины по каждой группе: 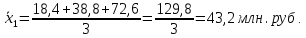 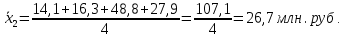 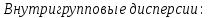 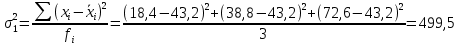 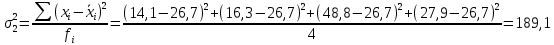 Средняя из внутригрупповых дисперсий: 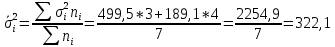 Определим общую среднюю величину для расчета межгрупповой дисперсии: 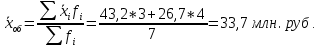 Межгрупповая дисперсия: 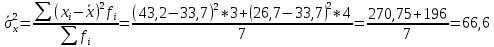 Общая дисперсия: 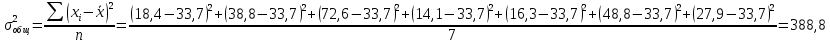 Б) Коэффициент детерминации: 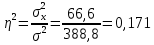 Эмпирическое корреляционное отношение: 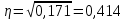 Вывод: эмпирическое корреляционное отношение равно 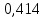 , значит теснота связи является умеренной ,т.к. 0,3<0,414<0,5. , значит теснота связи является умеренной ,т.к. 0,3<0,414<0,5.Распределение семей сотрудников компании по числу детей характеризуется следующими данными:
Определить: а) внутригрупповые дисперсии; б) среднюю из внутригрупповых дисперсий; в) межгрупповую дисперсию; г) общую дисперсию. Проверьте правильность произведенных расчетов с помощью правила сложения дисперсий и рассчитайте эмпирическое корреляционное отношение. А) Вычислим средние величины по каждой группы: 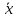 1= 1=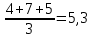 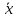 2= 2=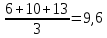 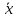 3= 3=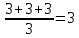 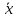 4= 4=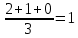 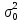 = =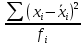 – Внутригрупповая дисперсия – Внутригрупповая дисперсия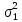 = = 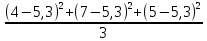 = 1,5 = 1,5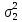 = =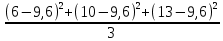 = 8,2 = 8,2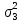 = =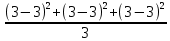 = 0 = 0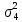 = =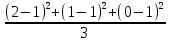 = 0,7 = 0,7Б) Средняя из внутригрупповых дисперсий: 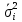 = =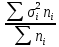 = = 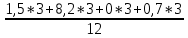 = 2,6 = 2,6В) Общая средняя величина для расчета межгрупповой дисперсии: 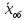 = =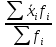 = = 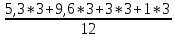 = 4,7 = 4,7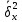 = = 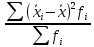 = = 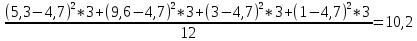 (межгрупповая дисперсия) (межгрупповая дисперсия)Г) Общая дисперсия: 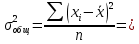 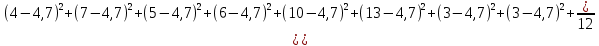 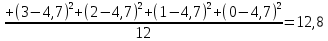 Проверим полученный результат, вычислив общую дисперсию по правилу сложения дисперсий: 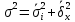 = 2,6+10,2=12,8 = 2,6+10,2=12,8Определим коэффициент детерминации: 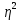 = =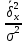 = = 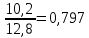 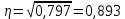 На основе данных таблицы рассчитать моду и медиану для интервального ряда.
Мода: Определим модальный интервал 25-30 тыс. руб.: 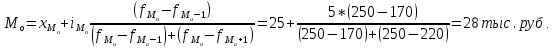 Медиана: Медианный интервал 25-30 тыс. руб.: 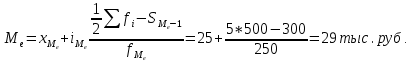 Численность занятых в экономике по возрасту распределилась следующим образом:
Определить медиану, первый и третий квартили, первый и девятый децили. Объясните их содержание. Медиана: 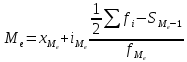 Медианный интервал: 40-44 (лет) Половина суммы частот = 100,0/2=50,0 Его накопленная частота – 66,1 Накопленная частота предшествующего интервала – 49,1 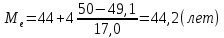 Квартиль: Qi 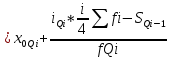 Первая квартиль (Q1) Q1= 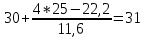 Третья квартиль (Q3) Q3 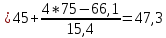 Децили:  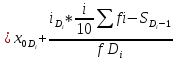 Первый децили D1: 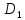 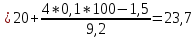 Девятый децили D9: 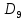 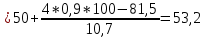 Вывод: Первый квартиль равен 31 и делит вариационный ряд на части, равные 25% и 75% соответственно. Третий квартиль равен 47,3 и делит вариационный ряд на части, равные 75% и 25% соответственно. Распределение вкладчиков банка по размерам срочных вкладов характеризуется следующими данными:
Для оценки степени децильной дифференциации вкладчиков определите все децили среднего размера вклада. Объясните их содержание. D= 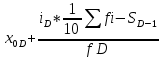 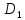 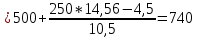 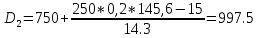 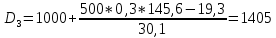 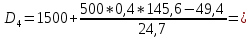 1700 1700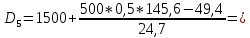 1974 1974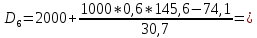 2431 2431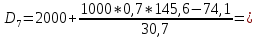 2906 2906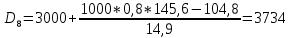 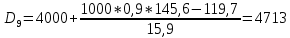 Вывод: 10% всех вкладов имеют сумму ниже 740 тыс. руб., половина вкладов имеют сумму выше 1974 тыс. руб., 10% вкладов имеют сумму более 4713 тыс. руб. При исследовании трудовой активности сотрудников организации (отработано человеко-дней за год) получены центральные моменты:
Используя показатели асимметрии и эксцесса, сравните характер распределения мужчин и женщин по трудовой активности. 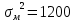 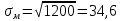 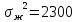 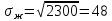 Мужчины: 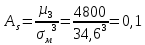 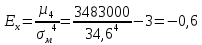 Женщины: 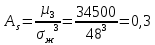 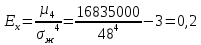 Вывод: Мужчины: A>0 асимметрия правосторонняя, Е<0 – распределение выборки плосковершинное, Женщины: A>0 асимметрия правосторонняя, E>0 – распределение выборки островершинное | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

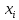
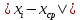
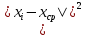
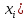
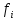 )
)