Расширение понятия числа. лекции Расширение понятия числа (1). Расширениепонятияо

• Название: Расширениепонятияо
• Анкор: Расширение понятия числа
• Дата: 31.01.2022
• Размер: 64.65 Kb.
• Имя файла: лекции Расширение понятия числа (1).docx
• Тип: Документы; #347190
• страница: 8 из 9

Переход от периодической дроби к обыкновенной

Пусть дана чистая периодическая дробь 0,(24), т.е. 0,242424…24… Обозначим соответствующее ей число через а. Если перенести запятую на две цифры вправо, число а увеличится в 100 раз и получим, что 100а=24,242424…24…, т.е. 100а=24+0,242424…24… = 24+а. Решая уравне-

ние 100а=24+а, получаем, что а= ²⁴ , т.е. а=

99

⁸ . Заметим, что 24 одновремен-

33

но и числитель дроби

²⁴ , и период дроби 0,(24).

99

Правило 1. При обращении в обыкновенную дробь чистой периодиче-ской десятичной дроби получается дробь, числитель которой равен периоду,а знаменатель состоит из такого числа девяток, сколько цифр в периодедроби.

Например, 0,(35)= ³⁵ .

99

Аналогично выводится правило для обращения в обыкновенную дробь

смешаннойпериодической десятичной дроби.

Правило 2. Если целая часть дроби равна нулю, то получается дробь,числитель которой равен разности между числом, записанным цифрами,стоящими до начала второго периода, и числом, записанным цифрами, сто-ящими до начала первого периода; знаменатель состоит из такого числа де-вяток, сколько цифр в периоде, и такого числа нулей, сколько цифр стоит доначала первогопериода.

Например, 0,7(61)= ^{761  7} = ³⁷⁷ .

990 495
Действительныечисла

11. 
    Понятие иррационального числа
    

Одним из источников появления десятичных дробей является деление натуральных чисел, другим – измерение величин. Выясним, как могут полу- чится десятичные дроби при измерении длины отрезка.

Пусть х– отрезок, длину которого надо измерить, е – единичный отрезок. Длину отрезка х обозначим Х, а длину отрезка е – Е. Пусть отрезок х состоит из n отрезков, равных е, и отрезка х₁, который короче отрезка е, т.е. nEX(n+1)E.

х

х₁

е

Числа n и n+1 есть приближенные значения длины отрезка х при едини- це длины Е с недостатком и с избытком с точностью до 1.

Чтобы получить ответ с большей точностью, возьмем отрезок е₁и будем укладывать его в отрезке х₁.При этом возможны два случая.

1. 
   Отрезок е₁уложился в отрезке х₁точно n раз. Тогда длина nотрезка хвы-
   

ражается конечной десятичной дробью: X=(n+ ⁿ¹ )E =

10


п, п₁

E. Например,

Х=3,4Е.

2. 
   Отрезок х₁оказывается состоящим из nотрезков, равных е₁, и отрезка х₂,
   

который короче отрезка е₁. Тогда
п, пE  X  п, пп^' E, где п, пи п, пп^' –

1 1 1 1 1 1

приближенные значения длины отрезка х с недостатком и с избытком с точ- ностью до 0,1.

Во втором случае процесс измерения отрезка х можно продолжать, взяв новый единичный отрезок е₂– сотую часть отрезка е.

На практике этот процесс измерения длины отрезка на каком-то этапе закончится. И тогда результатом измерения длины отрезка будет либо нату- ральное число, либо конечная десятичная дробь. Если же представить этот процесс измерения длины отрезка в идеале, то возможны два исхода:

1. 
   На k-том шагу процесс измерения окончится. Тогда длина отрезка хвыра-
   

зится конечной десятичной дробью вида п, п₁п₂ ...п_к.

2. 
   Описанный процесс измерения длины отрезка хпродолжается бесконечно.
   

Тогда отчет о нем можно представить символом вают бесконечной десятичной дробью.

п, п₁п₂ ...п_к... , который назы-

Итак, при измерении длин отрезков могут получаться бесконечные деся-

тичные дроби. Но всегда ли эти дроби периодические? Оказывается, что нет. Существуют отрезки, длины которых нельзя выразить бесконечной периоди- ческой дробью (т.е. положительным рациональным числом) при выбранной единицы длины. Это было важнейшим открытием в математике, из которого следует, что рациональных чисел недостаточно для измерения длин отрезков.

Теорема. Если единицей длины является длиной стороны квадрата, то длина диагонали этого квадрата не может быть выражена положительным рациональным числом.

Доказательство. Пусть длина стороны квадрата выражается числом 1. Предположим противное тому, что надо доказать, т.е. что длина диагонали

квадрата выражается несократимой дробью

^m. Тогда по теореме Пифагора,

n

выполнялось бы равенство 1² +1² = ^m2

_n2

. Из него следует, что m²=2n²,значит,

m²– четное число, тогда и число m – четное (квадрат нечетного числа не мо- жет быть четным). Итак, m = 2р. Заменив в равенстве m²=2n²число m на 2р, получаем, что 4р² = 2n², т.е. 2р²=n². Отсюда следует, что n²– четное, следо- вательно, n– четное число. Таким образом, числа n и m– четные, значит,

дробь

^mможно сократить на 2, что противоречит предположению о ее

n

несократимости. Установленное противоречие доказывает, что если едини-

цей длины является длина стороны квадрата, то длину диагонали этого квад- рата нельзя выразить рациональным числом.

Из теоремы следует, что существуют отрезки, длины которых нельзя выразить положительным рациональным числом или, другими словами, за- писать в виде бесконечной периодической дроби. И значит, бесконечные де- сятичные дроби могут быть непериодическими.

Считают, что бесконечные непериодические десятичные дроби являются записью новых чисел – положительных иррациональных чисел. Поэтому го- ворят, что бесконечные непериодические десятичные дроби – это и есть по- ложительные иррациональные числа.

Итак, получено понятие положительного иррационального числа через процесс измерения длин отрезков. Но иррациональные числа можно полу- чить и при извлечении корней из некоторых рациональных чисел. Например,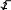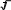

, – это иррациональные числа. Иррациональными являются также lg 5,

sin 31, числа =3,14…, е=2,7828… и другие.

^{Множество положительных иррациональных чисел обозначают J}+^.