Лекции по гидростатике. Определение предмета. Краткие исторические сведения

• Название: Определение предмета. Краткие исторические сведения
• Дата: 22.02.2022
• Размер: 1.47 Mb.
• Имя файла: Лекции по гидростатике.doc
• Тип: Документы; #370303
• страница: 3 из 4

2.7. ЭПЮРЫ ГИДРОСТАТИЧЕСКОГО ДАВЛЕНИЯ

Для многих задач расчета строительных конструкций требуется знать нагрузку со стороны жидкости на эту конструкцию. Значит, требуется знать, как действует гидростатическое давление в каждой точке поверхности конструкции. Графическое изображение изменения гидростатического давления вдоль рассматриваемой поверхности называется эпюрой давления.

Для построения эпюры гидростатического давления воды на плоскую поверхность в крайних точках этой поверхности восстанавливают перпендикуляры в виде стрелок, направленных со стороны жидкости к поверхности и имеющих длину, выраженную в масштабе рассматриваемого давления в этих точках. Чаще всего откладывают значение избыточного (манометрического) давления. Концы перпендикуляров соединяют прямой линией (изменение давления вдоль плоской поверхности имеет линейный характер, так как ).Получается геометрическая фигура, внутри которой осуществляют штриховку стрелками, направленными к рассматриваемой поверхности (рис. 2.11). Каждая такая стрелка изображает в масштабе значение гидростатического давления в точке, к которой направлена стрелка.

Построим эпюру избыточного давления на вертикальную (боковую стенку бассейна, заполненного водой глубиной Н (рис. 2.11, а).

Значение избыточного давления , в т. А , в т. В ; соединив концы стрелок-перпендикуляров прямой линией и заштриховав полученный треугольник стрелками, получим эпюру избыточного давления на поверхности АВ бассейна. Длина стрелки ef на эпюре выражает в масштабе значение манометрического давления в точке f стенки бассейна на глубине .

Аналогичным образом построены эпюры давления на поверхностях АВ, ВС, ADсоответствующих конструкций, показанных на рис. 2.11, б, в.

На рис. 2.11, г показан порядок построения результирующей эпюры избыточного давления (AC'dB) на плоскую пластину, перегораживающую канал глубиной 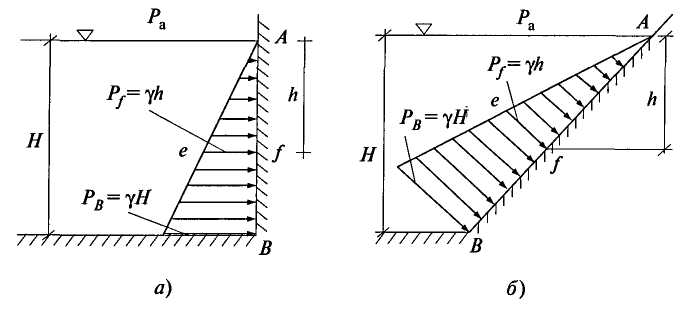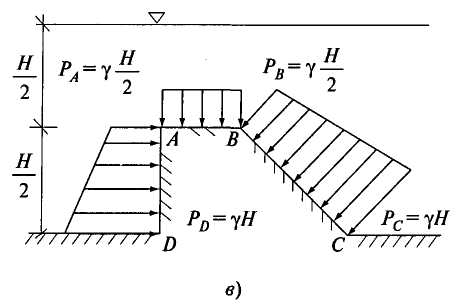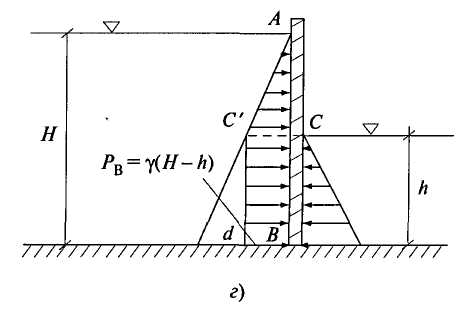перед пластиной и - за пластиной.





Рис. 2.11. Построение эпюр избыточного давления
2.8. СИЛА ДАВЛЕНИЯ ЖИДКОСТИ НА ПЛОСКУЮ ПОВЕРХНОСТЬ

Пусть некоторая плоская поверхность площадью 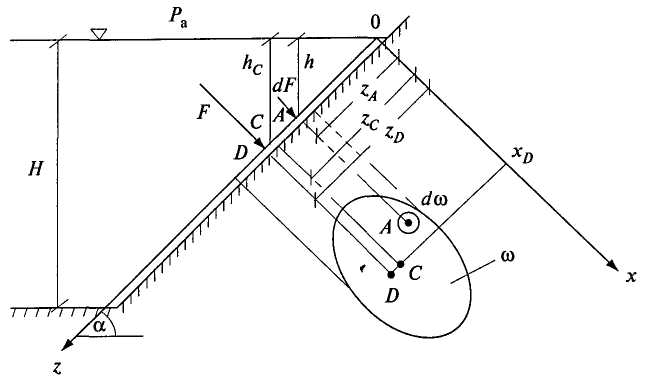сложной геометрической, формы лежит в пределах координатной плоскости xOz, имеющей наклон к горизонту под углом (рис. 2.12). Над поверхностью находится жидкость глубиной Н.



Рис. 2.12

Ось Ох лежит на линии пересечения координатной плоскости и свободной поверхности жидкости (т.е. ось Ох перпендикулярна плоскости чертежа). Определим результирующую силу избыточного давления жидкости на эту плоскую поверхность.

Для того чтобы видеть форму площадки и иметь возможность наносить на нее нужные обозначения, развернем координатную плоскость xOzвокруг оси Ozи совместим с плоскостью чертежа.

Выделим элементарную площадку в пределах поверхности около некоторой т. А, находящейся на глубине h. Сила избыточного давления на эту элементарную площадку ,где - среднее значение давления в пределах на глубине h, . Тогда , а суммарное давление на всю поверхность определится как



Выразим h через координату т. А по оси (z) и угол наклона поверхности ( ):



тогда



Произведение вынесено за знак интеграла как постоянная величина. Из теоретической механики известно, что представляет собой статический момент площади относительно оси Ох. Статический момент равен произведению площади на плечо, равное расстоянию от оси Ох до центра тяжести поверхности. На рис. 2.12 центр тяжести обозначен т.С.



тогда

(2.9)

Но - гидростатическое давление в центре тяжести рассматриваемой поверхности (h_c- глубина погружения центра тяжести площадки под уровень свободной поверхности).

Уравнение (2.9) показывает, что результирующая сила давления жидкости на любую плоскую площадку равна произведению гидростатического давления в центре тяжести этой площадки на ее площадь.

Если требуется определить силу абсолютного давления на плоскую поверхность, то формула для Fбудет иметь следующий вид:

(2.10)
2.9. ЦЕНТР ДАВЛЕНИЯ

Точка приложения результирующей силы давления жидкости на любую поверхность называется центром давления.

Применительно к рис. 2.12 центром давления является т. D. Определим координаты центра давления (x_D; z_D) для любой плоской поверхности.

Из теоретической механики известно, что момент равнодействующей силы относительно произвольной оси равен сумме моментов составляющих сил относительно той же оси. За ось в нашем случае примем ось Ох (см. рис. 2.12), тогда



Известно также, что является моментом инерции площади относительно оси Ox

В результате получаем



откуда



Подставим в это выражение формулу (2.9) для Fи геометрическое соотношение :



Перенесем ось момента инерции в центр тяжести площадки . Обозначим момент инерции относительно оси, параллельной оси Ох и проходящей через т.С, через . Моменты инерции относительно параллельных осей связаны соотношением

;

тогда и окончательно получим

(2.11)

Формула показывает, что центр давления расположен всегда ниже центра тяжести площадки, за исключением случая, если площадка горизонтальна и центр давления совпадает с центром тяжести. Для простых геометрических фигур моменты инерции относительно оси, проходящей через центр тяжести и параллельной оси Ох (рис. 2.12), определяются по следующим формулам:

для прямоугольника

(2.12)

где сторона основания параллельна Ох;

для равнобедренного треугольника

(2.13)

где сторона основания параллельна Ох;

для круга

(2.14)

Координата 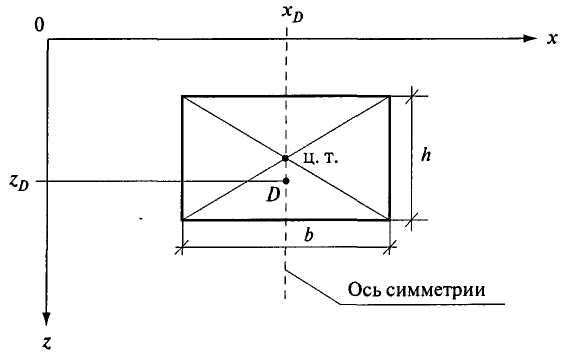для плоских поверхностей строительных конструкций чаще всего определяется по координате расположения оси симметрии геометрической фигуры, ограничивающей плоскую поверхность. Так как такие фигуры (круг, квадрат, прямоугольник, треугольник) имеют ось симметрии, параллельную координатной оси Oz, местоположение оси симметрии и определяет координату x_D. Например, для прямоугольной плиты (рис. 2.13), определение координаты x_Dясно из чертежа.



Рис. 2.13. Схема расположения центра давления для прямоугольной поверхности

Гидростатический парадокс. Рассмотрим силу давления жидкости на дно сосудов, изображенных на рис. 2.14.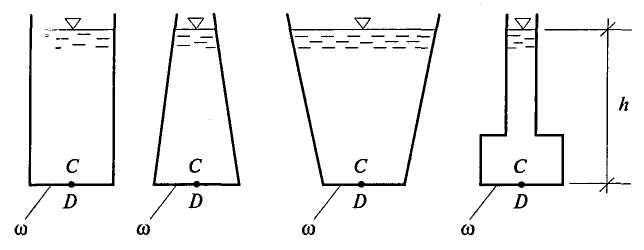



Рис. 2.14. Сила давления на дно сосудов различных форм

Несмотря на разную форму объемов сосудов, изображенных на этом рисунке, сила давления на дно каждого из них будет одинакова, хотя вес налитой в каждый объем жидкости будет различен. Действительно, , но и h_cдля всех сосудов одинаковы.
2.10. ДАВЛЕНИЕ ЖИДКОСТИ НА КРИВОЛИНЕЙНЫЕ ПОВЕРХНОСТИ

Рассмотрим некоторую криволинейную твердую бесконечно тонкую поверхность 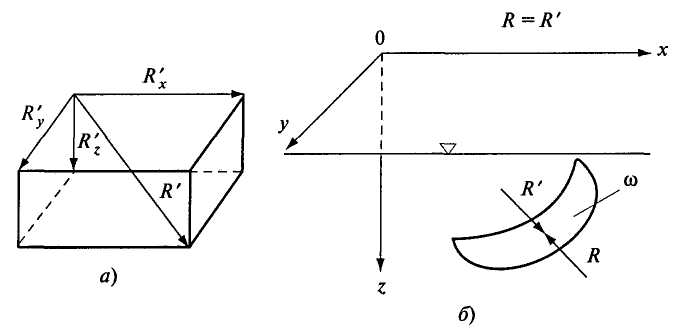, находящуюся на некоторой глубине покоящейся жидкости (рис. 2.15). Координатные плоскости расположены, как показано на рисунке. Плоскость хОу лежит и пределах свободной поверхности жидкости. Ось Ozнаправлена вниз. На поверхности действуют две силы Rи R', равные между собой и направленные навстречу друг другу.



Рис. 2.15. К определению результирующей силы давления

Любую из этих сил можно разложить на три составляющие. Например, для силы R' это R'_x, R'_y, R'_z (рис. 2.14, а). Тогда искомая сила

(2.15)

Определим сначала силу R_z. Для этого через контур поверхности 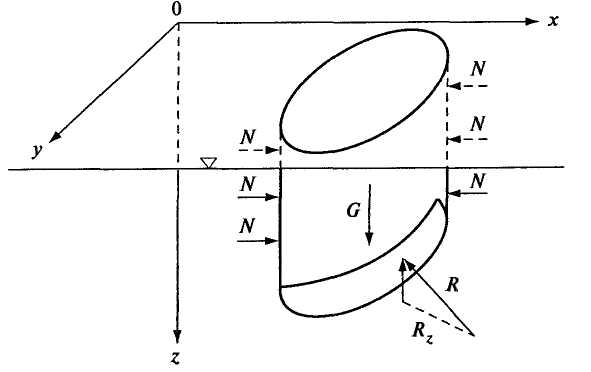вертикально вверх проведем цилиндрическую поверхность до пересечения со свободной поверхностью жидкости (рис. 2.16).



Рис. 2.16. К определению вертикальной составляющей силы давления

Для того чтобы выделенный жидкий цилиндр находился в равновесии, должны выполняться следующие условия: ; ; .

Но так как сила входит только в третье уравнение, рассмотрим это уравнение: .

Из поверхностных сил будем рассматривать силы избыточного давления, т.е. исключим из рассмотрения . Получаем

,

где - вес жидкости в объеме цилиндра, ограниченного свободной поверхностью жидкости и криволинейной поверхностью . Отсюда

,(2.16)

где - объем цилиндра.

В результате получим, что вертикальная составляющая давления жидкости на криволинейную поверхность равна весу жидкости в объеме вертикального цилиндра, нижним основанием которого является сама криволинейная поверхность, а верхним основанием - свободная поверхность жидкости. Выделенный объем жидкого цилиндра называют телом давления ( ).

Определим горизонтальные составляющие силы 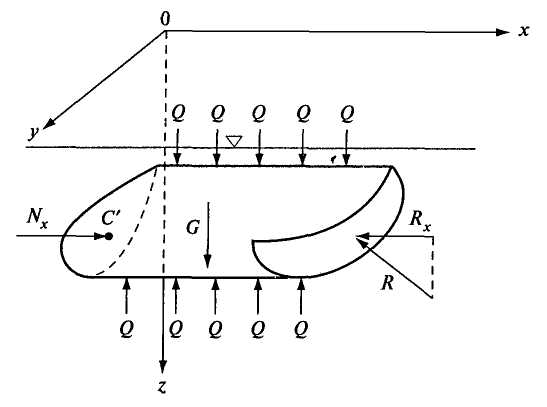, т.е. и . Для определения выполним построение горизонтального цилиндра, ограниченного с одной стороны поверхностью , и с другой стороны - координатной плоскостью (рис. 2.17).



Рис. 2.17. К определению горизонтальной составляющей силы давления

Аналогично предыдущим рассуждениям силы , в проекции на ось обращаются в ноль. В рассмотрении остается уравнение .

,

где - сила давления на поверхность, образованную пересечением координатной плоскости и цилиндрической поверхности. Обозначим площадь этой плоской поверхности и обратим внимание на то, что является проекцией криволинейной поверхности на вертикальную плоскость, параллельную .

,

где - глубина погружения центра тяжести площади под уровень свободной поверхности жидкости.

В результате получим .

. (2.17)

Так как составляющая горизонтальна, аналогичные рассуждения приводят к равенству

(2.18)

где - площадь проекции криволинейной поверхности на вертикальную плоскость, параллельную координатной плоскости ; - глубина погружения центра тяжести под уровень свободной поверхности жидкости.

Таким образом, три составляющие для определения результирующей силы давления жидкости на криволинейную поверхность будут:

; ; .

Сила 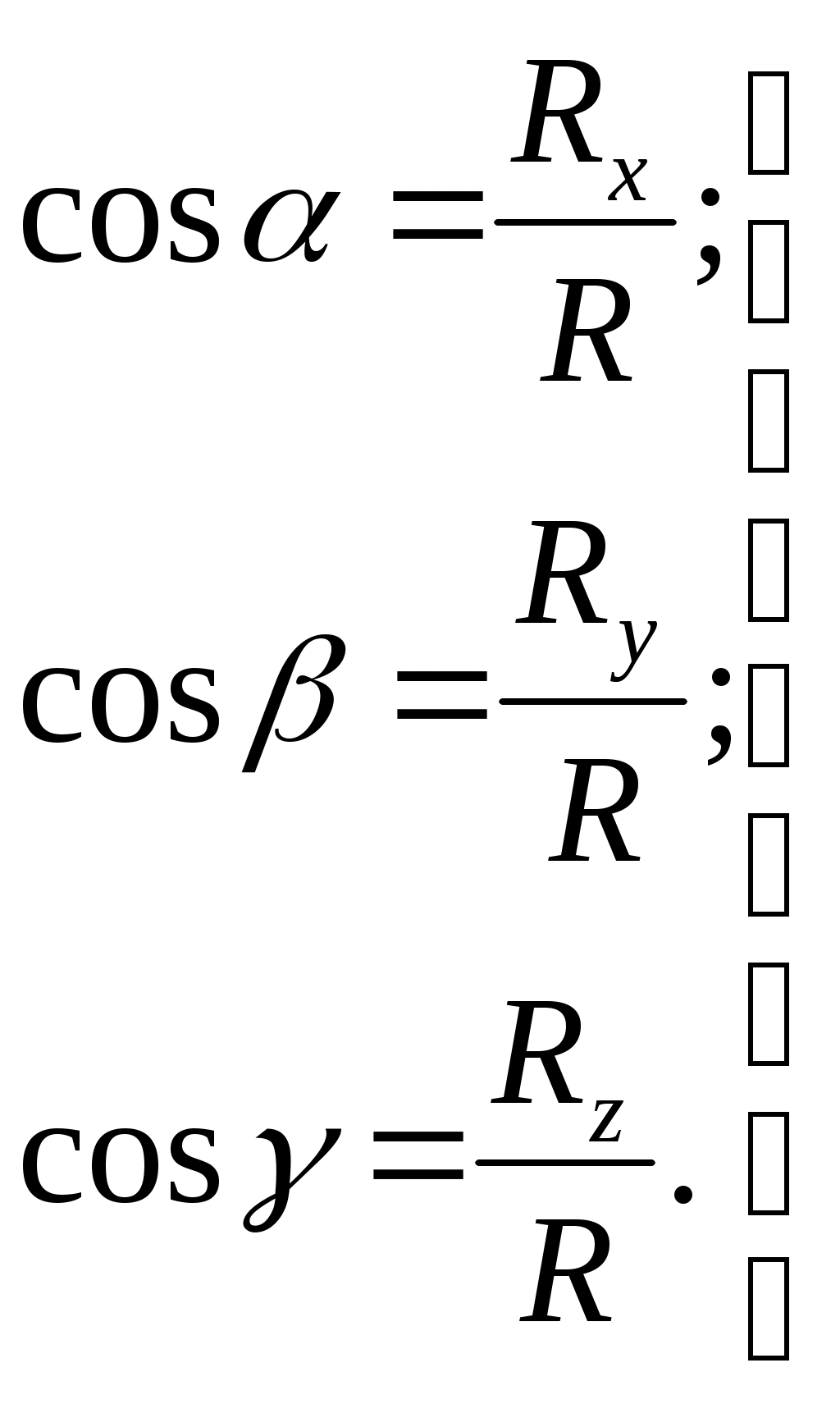находится по формуле (2.15), а направление силы определяется по углам , , между силой и соответствующей проекцией силы (см. рис. 2.18, а):

. (2.19)

Рассмотрим два примера определения силы давления жидкости на цилиндрические поверхности.