Лекции по гидростатике. Определение предмета. Краткие исторические сведения

• Название: Определение предмета. Краткие исторические сведения
• Дата: 22.02.2022
• Размер: 1.47 Mb.
• Имя файла: Лекции по гидростатике.doc
• Тип: Документы; #370303
• страница: 2 из 4

2.2. ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ И ЕГО СВОЙСТВА

Одним из основных понятий гидростатики является понятие гидростатического давления. Для его объяснения рассмотрим некоторый объем жидкости, находящийся в равновесии (рис. 2.3).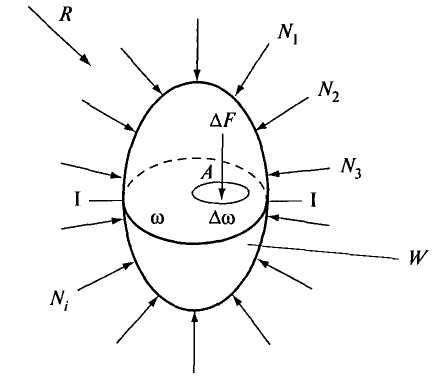



Рис. 2.3. К определению понятия гидростатического давления

Проведем секущую плоскость I-I, которая разделит объем Wна две части, и отбросим мысленно одну из них, например верхнюю. Действие отброшенной части на нижнюю заменим распределенными по поверхности силами . На площадку действует сила . Представим, что «стягивается» в т. А. Тогда предел отношения при называется гидростатическим давлением в рассматриваемой точке

. (2.1)

Следует отметить, что этот же предел отношения 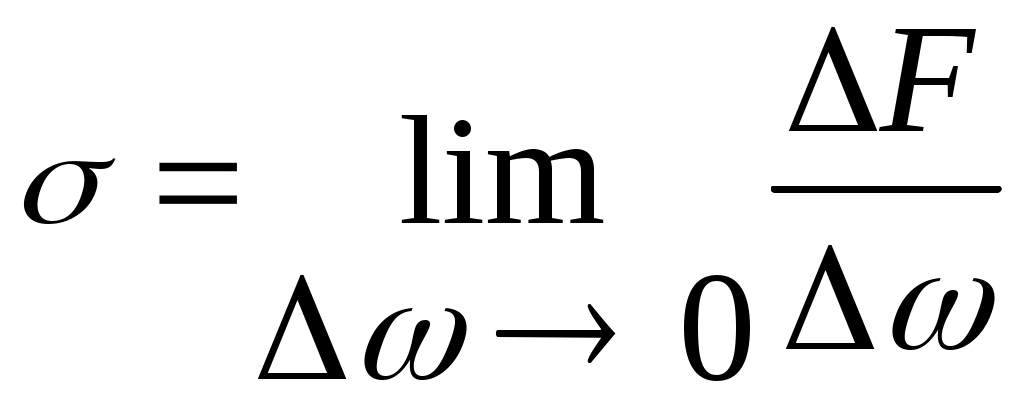в курсе сопротивления материалов носит название упругого напряжения сжатия :

.

Таким образом, гидростатическое давление в рассматриваемой точке жидкости есть упругое напряжение сжатия, возникающее в жидкости под действием внешних сил. В качестве единицы измерения этой величины применяют 1 Па (один паскаль). Под 1 Па понимают давление, создаваемое силой в 1 Н, которая равномерно распределена по поверхности площадью 1 м².

Рассмотрим свойства гидростатического давления.

Так как сила , использованная в данном определении понятия гидростатического давления, должна быть перпендикулярна площадке , так как жидкость находится в равновесии, то и гидростатическое давление должно быть направлено со стороны жидкости по нормали к той поверхности, на которую действует. Это и является первым свойством гидростатического давления.

Выделим из покоящейся жидкости, находящейся в условиях темного тяготения, элементарный объем в виде кубика со сторонами dx, dy, dz(рис. 2.4). Оси координат направим параллельно сторонам.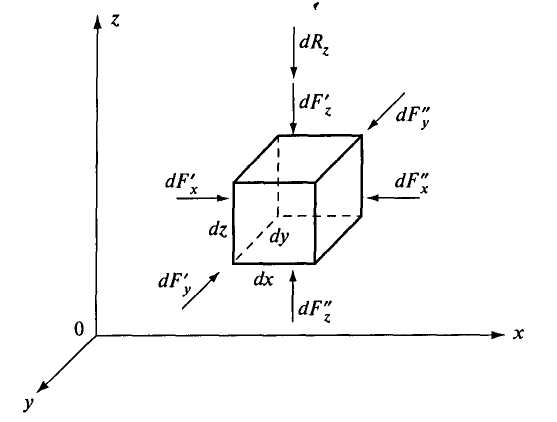



Рис. 2.4. Действие внешних сил на объем жидкости в виде элементарного кубика

Кубик находится в равновесии, значит, уравновешены поверхностные и массовые силы, действующие на кубик по всем трем осям х, у, z:

.

Для условий земли единственной массовой силой Rявляется сила тяжести, т.е. в рассматриваемом случае 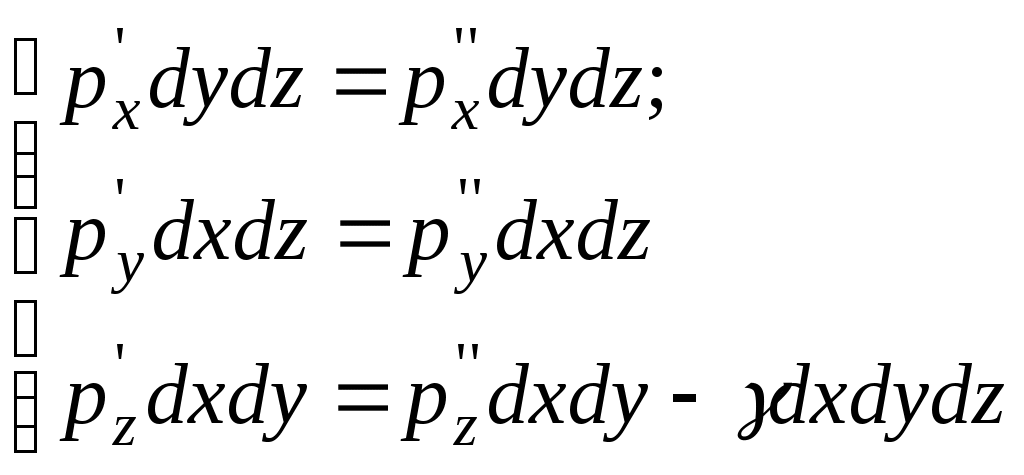, где - объем кубика.

Так как , систему уравнении можно записать в следующем виде:



Сократив равенства, получим: .

Членом по сравнению с можно пренебречь как величиной бесконечно малой. Получаем, что .

Выделенный кубик не деформируется, находясь в условиях равновесия, значит .

В результате логично сделать вывод: так как кубик бесконечно мал и выбран в произвольном месте, то и для любой точки жидкости гидростатическое давление одинаково по всем направлениям - это и есть второе свойство гидростатического давления.

Из этого свойства вытекает следствие: так как любая точка определяется ее координатами, гидростатическое давление в точке зависит от координат рассматриваемой точки:
2.3. ОСНОВНОЕ УРАВНЕНИЕ ГИДРОСТАТИКИ

Определим, каким образом гидростатическое давление зависит от места расположения точки, в которой определяется давление. Для этого выделим из покоящейся жидкости (рис. 2.5), заполняющей резервуар 1, параллелепипед 2 с основанием 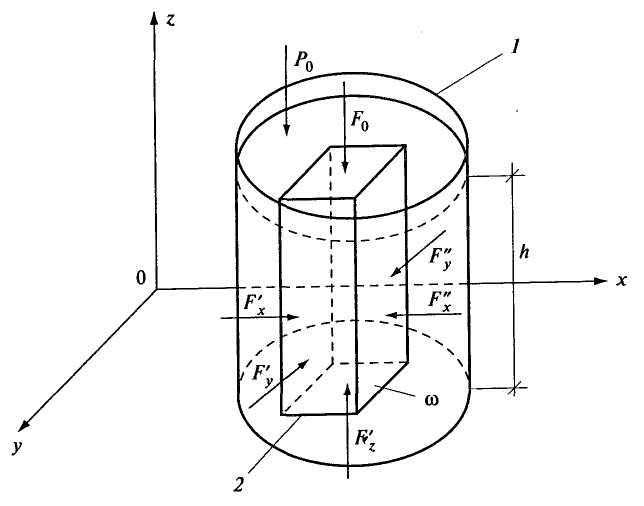и высотой , равной глубине жидкости в резервуаре. Пусть на поверхности жидкости в резервуаре в условиях земного тяготения действует давление . Так как жидкость находится в равновесии: , а сила , действующая на дно параллелепипеда, уравновешивается силой и силой веса жидкости, находящейся в объеме параллелепипеда,

( и - объем параллелепипеда).



Рис. 2.5. К выводу основного уравнения гидростатики

Разделив это уравнение на и зная, что и , получим

(2.2)

где p - гидростатическое давление на глубине h; - внешнее давление на поверхности жидкости.

Это уравнение называется основным уравнением гидростатики. Каждый член этого уравнения имеет свое название.

Произведение называется весовым давлением . В свою очередь, весовое давление , если внешнее давление равно атмосферному давлению, , называется избыточным давлением: .
2.4. ПОВЕРХНОСТЬ РАВНОГО ДАВЛЕНИЯ. ЗАКОН ПАСКАЛЯ

Поверхностью равного давления называется поверхность, в каждой точке которой величина гидростатического давления одинакова (p=const). Например, на поверхности жидкости, соприкасающейся с атмосферой, давление равно p_а. Такая поверхность равного давления называется свободной поверхностью. На рисунках данного учебника свободная поверхность обозначается значком . Абсолютное гидростатическое давление в жидкости на глубине hопределяется уравнением (2.2) . Для поверхности равного давления, если внешнее давление p₀=const, получаем =const. Так как произведение =const, последнее равенство определяет положение поверхности равного давления для покоящейся жидкости в условиях Земли: h=const. Любая горизонтальная поверхность в пределах жидкости является поверхностью равного давления или поверхностью уровня.

Из основного уравнения (2.2) следует, что в случае изменения внешнего давления p_ово всех точках жидкости, находящейся в равновесии, давление p изменится на ту же величину. Это свойство жидкости определяет закон Паскаля, который можно сформулировать следующим образом: внешнее давление на свободной поверхности жидкости, находящейся в равновесии, передается во все точки жидкости без изменения по всем направлениям.
2.5. ГЕОМЕТРИЧЕСКОЕ И ЭНЕРГЕТИЧЕСКОЕ ПОНЯТИЯ ОСНОВНОГО УРАВНЕНИЯ ГИДРОСТАТИКИ

Преобразуем уравнение (2.2), записав значение (рис. 2.6).

Для любой точки, например т. А,



где z- координата т. A; - координата свободной поверхности.

Получим





Разделим обе части полученного уравнения на величину 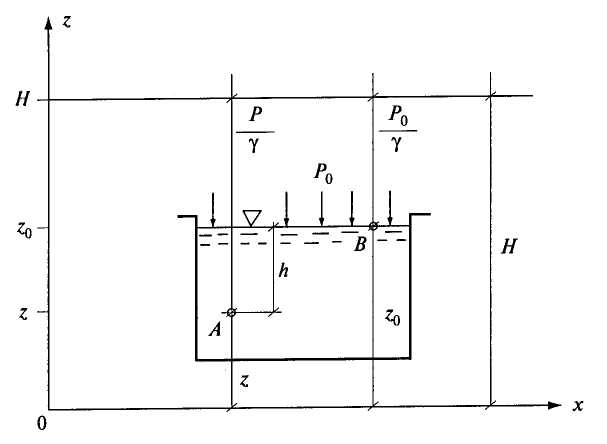и сделаем перестановки слагаемых:

(2.3)



Рис. 2.6. Геометрическое пояснение основного уравнения гидростатики

Уравнение (2.3) также носит название основного уравнения гидростатики, но оно представлено в другой форме записи.

Каждый член этого уравнения имеет размерность метр: м; м. Значит, уравнение (2.3) можно представить как уравнение высот, в котором

- высота положения точки (геометрический напор);

- высота, соответствующая давлению (напор).

Так как и для рассматриваемого резервуара - величины конкретные, можно записать

(2.4)

Величину Н называют гидростатическим (потенциальным) напором. Эта величина одинакова для любой точки жидкости, находящейся в рассматриваемом резервуаре с постоянными и .

Плоскость xOzназывают плоскостью сравнения или начальной плоскостью.

Но уравнение (2.3) легко выразить в единицах энергии, для этого достаточно умножить каждый член уравнения на 1 Н (ньютон), тогда все слагаемые будут выражены в единицах энергии (Дж=Н м). Значит, каждое слагаемое уравнения (2.3) представляет собой вид потенциальной энергии, так как жидкость находится в покое:

- удельная потенциальная энергия положения;

- удельная потенциальная энергия давления;

Н - полный запас удельной потенциальной энергии.

Слово «удельная» означает энергию, приходящуюся на единицу веса жидкости (на 1 Н). Следует отметить, что в гидравлике слово «напор» означает удельную энергию жидкости и может применяться наряду со словом «высота», так как имеет ту же размерность [м].
2.6. АБСОЛЮТНОЕ И ИЗБЫТОЧНОЕ ДАВЛЕНИЕ

Вернемся к основному уравнению гидростатики в форме записи (2.2):

.

Для покоящейся жидкости возможно три случая действия внешнего давления



Рассмотрим каждый из этих случаев.

1. На рис. 2.7 изображен закрытый резервуар, внутри которого помещена жидкость, на свободной поверхности которой создано давление . Для измерения давления сбоку от резервуара на высоте hот поверхности установлена стеклянная трубочка с открытым верхним концом, которая называется пьезометром. Под действием давления в резервуаре вода в стеклянной трубочке поднимается на высоту , а на поверхности воды в трубочке будет давление . На рисунке 0-0 - плоскость сравнения; 1-1 - уровень жидкости, где давление в любой точке будет такое же, что и в т. А.

Для случая, изображенного в на рис. 2.7, в точке А согласно (2.2) абсолютное гидростатическое давление , где 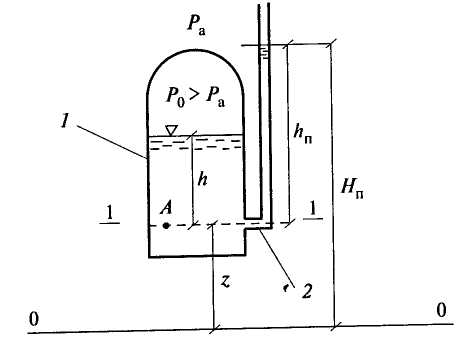- весовое давление . С другой стороны, для любой точки уровня 1-1 со стороны пьезометра давление запишется так:



где - избыточное давление ; - высота, называемая пьезометрической высотой.



Рис. 2.7. Резервуар с жидкостью, на поверхности которой

Но ,так как жидкость находится в состоянии покоя, т.е. тогда

(2.5)

а пьезометрическая высота

(2.6)

Высота называется пьезометрическим напором.

Для данного случая действия внешнего давления избыточное давление есть величина положительная и имеет специальное название - манометрическое давление - по названию приборов заводского изготовления, манометров, которые по своим конструктивным особенностям способны измерять (как правило) только избыточное давление



Как отмечалось в п. 2.1, единицей измерения давления в системе СИ является 1 Па, но на практике часто используются и другие единицы измерения, например «техническая атмосфера» — 1 ат.

1ат = 1 кгс/см² или при переводе в систему СИ 1 ат = 9,8 10⁴Па= 100 000 Па.

Из наших рассуждений следует, что давление можно измерять и высотой столба жидкости .

Для воды с плотностью кг/м³ 1 ат = 10 м вод. Для ртути с плотностью кг/м³ 1 ат=0,7382 м рт.ст.=738,2 мм рт.ст.

1 Па = 0,102 10^-3 м вод. ст.

1 Па = 0,00752 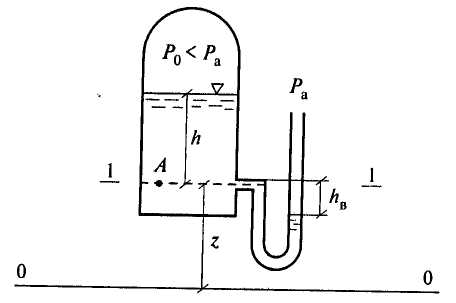10^-3 м рт. ст. = 0,00752 мм рт. ст.

2. На поверхности жидкости в закрытом резервуаре путем откачки воздуха или газа создано давление (рис. 2.8) На глубине hсбоку от резервуара на уровне 1-1 установлен так называемый обратный пьезометр или, что то же, вакуумметр в виде U-образной стеклянной трубки с открытым верхним концом. Глубину hвыберем таким образом, чтобы весовое давление на этой глубине было меньше разности .



Рис. 2.8. Резервуар с жидкостью, на поверхности которой

Тогда уровень жидкости в обратном пьезометре будет ниже уровня 1-1 ( ).

Согласно (2.2) но, с другой стороны, на уровне 1-1 в обратном пьезометре давление . Соединив знаком равенства приведенное выражение ( ), получим .

В данном случае избыточное давление является отрицательной величиной.

Если избыточное давление отрицательно, говорят, что в данной точке образуется вакуумм. Вакуумм - это недостаток давления в данной точке до атмосферного



Величину называют вакуумметрической высотой:

(2.8)

Для измерения часто используют и другой тип вакуумметра (рис. 2.9).



Рис. 2.9. Вакуумметр

Один конец стеклянной трубочки подсоединен к точке, где определяется вакуумметрическое давление, а другой опущен в жидкость со свободной поверхностью, на которой _.

Уровень жидкости в стеклянной трубочке поднимается на высоту , так как давление над уровнем 1-1 в трубке равно абсолютному давлению , а ниже уровня 1-1 отсюда .

Вакуумметрическое давление измеряется в единицах давления - Па.

Величина будет определяться значением плотности жидкости в вакуумметре.

Для воды значение не должно превышать 10 м, так как избыточное давление на глубине 10 м воды равно 1 ат.

Если в рассматриваемой точке м вод. ст., то это значит, что абсолютное давление в этой точке будет соответствовать м вод. ст.

3. Рассмотрим случай с открытым резервуаром, заполненным жидкостью, на свободной поверхности которой давление (рис. 2.10).

Для измерения давления на глубине hустановлен пьезометр, уровень жидкости в котором, очевидно, поднимется до уровня свободной поверхности жидкости в резервуаре.



Рис. 2.10. Резервуар с жидкостью, на поверхности которой

Согласно формуле (2.2) , но, с другой стороны, Так как и , для открытого резервуара весовое ( ) и избыточное давление ( ) равны ( ).

Эта схема действия внешнего давления на поверхности жидкости является основной для условий строительного производства, водоподающих и водоочистных систем. Особенностью этой схемы является то, что внешнее давление для расчетных случаев известно, т.е. Поэтому основной расчетной величиной для различных задач будет являться избыточное давление. Довольно часто в расчетной практике под гидростатическим давлением в точке понимается величина избыточного давления, при этом индекс «изб» в обозначении давления опускается ( ), а понятие весового давления совсем не используется.