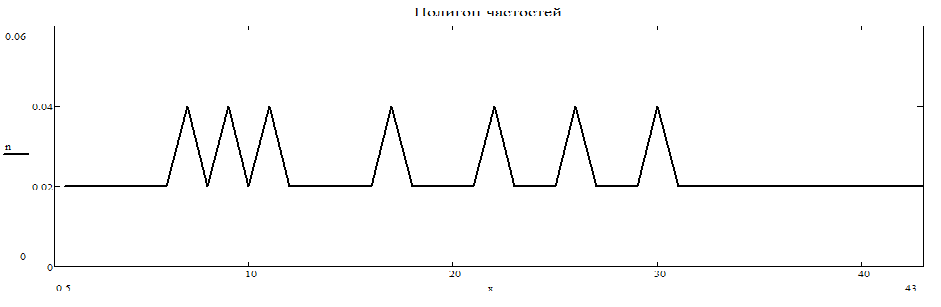
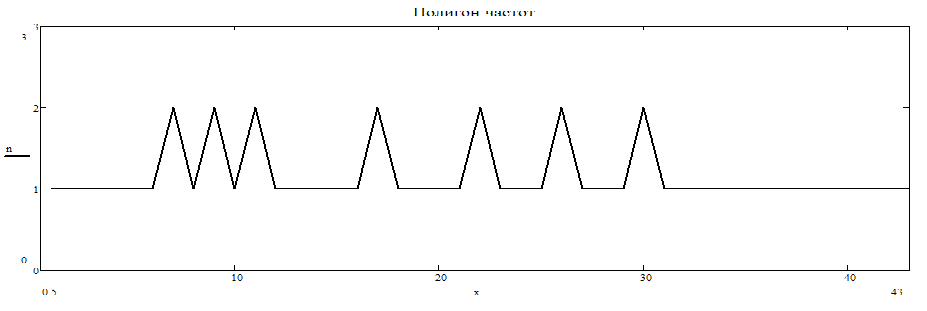
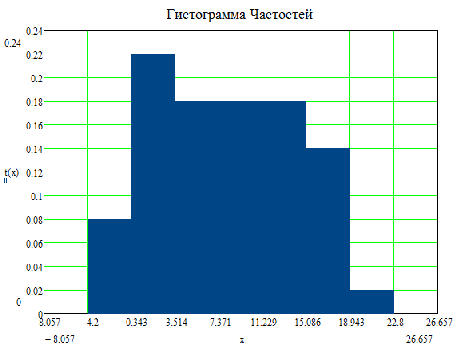
   1. Вариационный ряд: 1. Вариационный ряд:
-4.2, -2.0, -1.0, -0.7, -0.2, 0.4, 1.4, 1.4, 1.7, 2.4, 2.4, 3.0, 3.1, 3.1, 3.4, 3.8, 4.3, 4.6, 5.6, 5.7, 5.7, 6.1, 6.7, 7.1, 8.1, 8.2, 8.2, 9.2, 9.8, 10.0, 10.5, 10.5, 10.6, 12.0, 12.3, 12.6, 12.6, 14.0, 14.2, 14.3, 14.5, 14.9, 15.8, 16.0, 16.1, 17.5, 18.3, 18.5, 18.9, 22.8
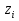
|
[-4.2 ; -0.343)
|
[-0.343 ; 3.514)
|
[3.514 ; 7.371)
|
[7.371 ; 11.228)
|
[11.228 ; 15.085)
|
[15.085 ; 18.942)
|
[18.942 ; 22.8]
|
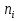
|
4
|
11
|
9
|
9
|
9
|
7
|
1
|
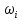
|
0.08
|
0.22
|
0.18
|
0.18
|
0.18
|
0.14
|
0.02
|
2. Интервальный статистический ряд:
3-4. Частота и частость.
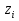
|
-4,2
|
-2,0
|
-1,0
|
-0,7
|
-0,2
|
0,4
|
1,4
|
1,7
|
2,4
|
3,0
|
3,1
|
3,4
|
3,8
|
4,3
|
4,6
|
5,6
|
5,7
|
6,1
|
6,7
|
7,1
|
8,1
|
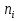
|
1
|
1
|
1
|
1
|
1
|
1
|
2
|
1
|
2
|
1
|
2
|
1
|
1
|
1
|
1
|
1
|
2
|
1
|
1
|
1
|
1
|
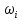
|
1/50
|
1/50
|
1/50
|
1/50
|
1/50
|
1/50
|
2/50
|
1/50
|
2/50
|
1/50
|
2/50
|
1/50
|
1/50
|
1/50
|
1/50
|
1/50
|
2/50
|
1/50
|
1/50
|
1/50
|
1/50
|
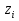
|
8,2
|
9,2
|
9,8
|
10,0
|
10,5
|
10,6
|
12,0
|
12,3
|
12,6
|
14,0
|
14,2
|
14,3
|
14,5
|
14,9
|
15,8
|
16,0
|
16,1
|
17,5
|
18,3
|
18,5
|
18,9
|
22,8
|
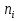
|
2
|
1
|
1
|
1
|
2
|
1
|
1
|
1
|
2
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
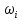
|
2/50
|
1/50
|
1/50
|
1/50
|
2/50
|
1/50
|
1/50
|
1/50
|
2/50
|
1/50
|
1/50
|
1/50
|
1/50
|
1/50
|
1/50
|
1/50
|
1/50
|
1/50
|
1/50
|
1/50
|
1/50
|
1/50
|
5-6. Накопленная частота и накопленная частость.
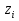
|
[-4.2 ; -0.343)
|
[-0.343 ; 3.514)
|
[3.514 ; 7.371)
|
[7.371 ; 11.228)
|
[11.228 ; 15.085)
|
[15.085 ; 18.942)
|
[18.942 ; 22.8]
|
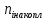
|
4
|
15
|
24
|
33
|
42
|
49
|
50
|
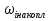
|
0.08
|
0.3
|
0.48
|
0.66
|
0.84
|
0.98
|
1
|
7. Выборочная функция распределения. 8. Размах выборки.
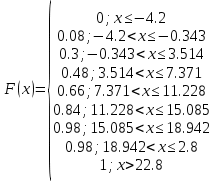 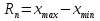 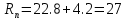
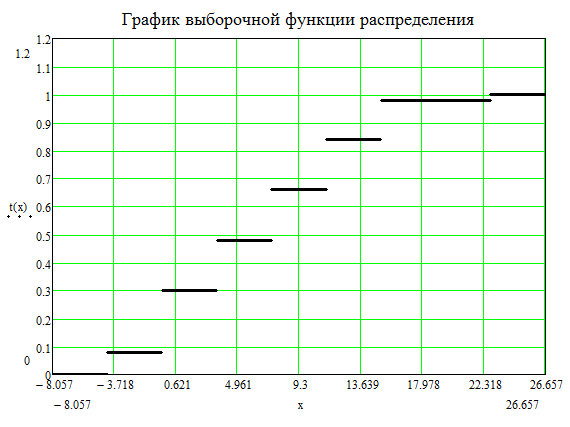 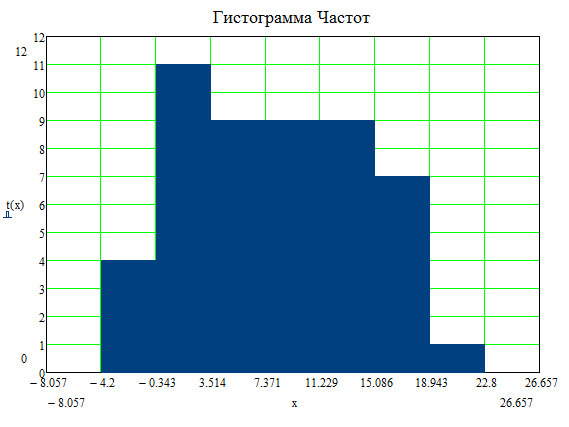
Найдем выборочное среднее для
А) несгруппированной СВ:
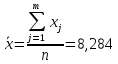
Б) сгруппированной СВ:
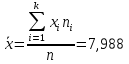
Найдем моду для
А) несгруппированной СВ: 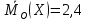
Б) сгруппированной СВ: 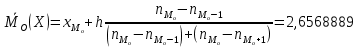
Найдем медиану для
А) несгруппированной СВ: 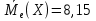
Б) сгруппированной СВ: 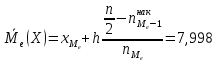
Найдем дисперсию для
А) несгруппированной СВ: 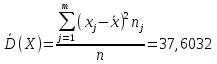
Б) сгруппированной СВ: 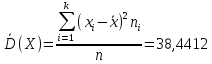
Найдем среднее квадратическое отклонение для
А) несгруппированной СВ: 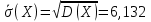
Б) сгруппированной СВ: 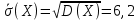
Найдем начальный момент первого порядка для
А) несгруппированной СВ: 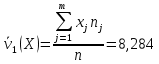
Б) сгруппированной СВ: 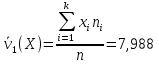
Найдем начальный момент второго порядка для
А) несгруппированной СВ: 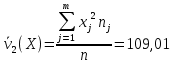
Б) сгруппированной СВ: 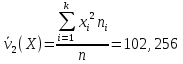
Найдем начальный момент третьего порядка для
А) несгруппированной СВ: 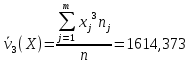
Б) сгруппированной СВ: 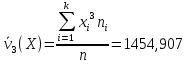
Найдем начальный момент четвертого порядка для
А) несгруппированной СВ:
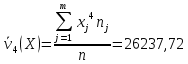
Б) сгруппированной СВ: 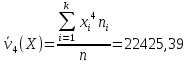
Найдем центральный момент первого порядка для
А) несгруппированной СВ: 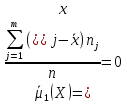
Б) сгруппированной СВ: 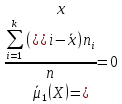
Найдем центральный момент второго порядка для
А) несгруппированной СВ: 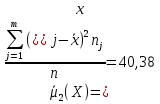
Б) сгруппированной СВ: 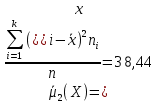
Найдем центральный момент третьего порядка для
А) несгруппированной СВ: 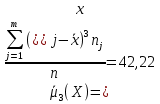
Б) сгруппированной СВ: 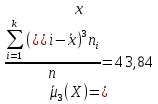
Найдем центральный момент четвертого порядка для
А) несгруппированной СВ: 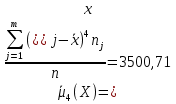
Б) сгруппированной СВ: 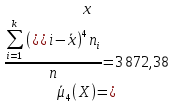
Найдем коэффициент асимметрии для
А) несгруппированной СВ: 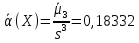
Б) сгруппированной СВ: 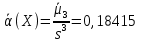
Найдем коэффициент эксцесса для
А) несгруппированной СВ: 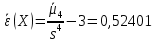
Б) сгруппированной СВ: 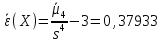
Числовая характеристика
|
Негруппированная СВ
|
Сгруппированная СВ
|
На сколько изменились выборочные характеристики после группировки
|
Во сколько раз изменились выборочные характеристики после группировки
|
Выборочное среднее
|
8,284
|
7,988
|
-0,296
|
0,964268
|
Мода
|
2,4
|
2,656
|
0,256
|
1,106667
|
Медиана
|
8,15
|
7,998
|
-0,152
|
0,98135
|
Дисперсия
|
37,6032
|
38,4412
|
0,838
|
1,022285
|
Среднеквадратичное отклонение
|
6,132
|
6,2
|
0,068
|
1,011089
|
Начальный момент I-го порядка
|
8,284
|
7,988
|
-0,296
|
0,964268
|
Начальный момент II порядка
|
109,01
|
102,256
|
-6,754
|
0,938042
|
Начальный момент III порядка
|
1614,373
|
1454,907
|
-159,466
|
0,901221
|
Начальный момент IV порядка
|
22237,72
|
22425,39
|
187,67
|
1,008439
|
Центральный момент I порядка
|
0
|
0
|
0
|
-
|
Центральный момент II порядка
|
40,38
|
38,44
|
-1,94
|
0,951956
|
Центральный момент III порядка
|
42,22
|
43,84
|
1,62
|
1,03837
|
Центральный момент IV порядка
|
3500,71
|
3872,38
|
371,67
|
1,10617
|
Коэффициент эксцесса
|
0,52401
|
0,37933
|
-0,14468
|
0,723898
|
Коэффициент асиметрии
|
0,18332
|
0,18415
|
0,00083
|
1,004528
| Вывод по лабораторной работе:
По виду гистограмм можно сделать предположение, что величины распределены по нормальному закону.
Из таблицы числовых характеристик видно, что:
а) Выборочное средне, медиана, дисперсия, среднеквадратичное отклонение, начальный момент I-го порядка, центральный момент I порядка ,центральный момент II порядка, центральный момент III порядка для несгруппированной и сгруппированной величин отличаются друг от друга не более чем на 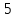 . .
б)Мода. начальный момент II порядка, начальный момент III порядка, центральный момент IV порядка – не более чем на 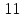 . .
ж) Самое большое различие у коэффициента эксцесса - 28%.
|
 Скачать 72.65 Kb.
Скачать 72.65 Kb.

 1. Вариационный ряд:
1. Вариационный ряд: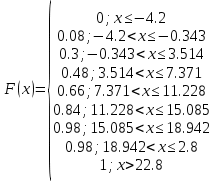
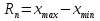
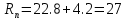


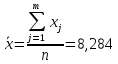
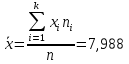

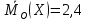

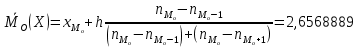

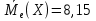

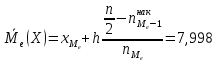

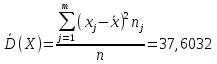

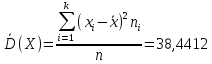

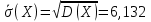

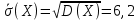

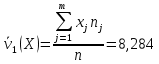

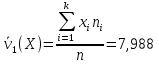

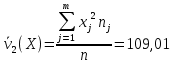

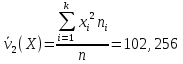

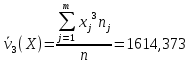

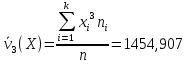
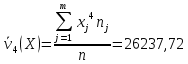

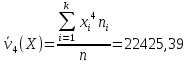

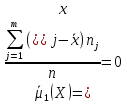

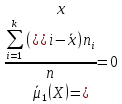

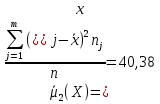

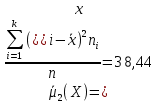

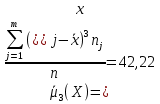

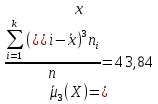

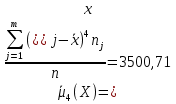

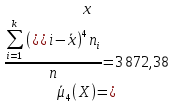

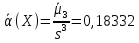

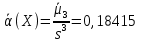

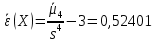

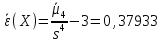

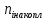
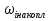
 .
.  .
.