21 Модель измерения. 2 Модель измерения и основные постулаты метрологии

• Название: 2 Модель измерения и основные постулаты метрологии
• Дата: 02.03.2019
• Размер: 71 Kb.
• Имя файла: 21 Модель измерения.doc
• Тип: Документы; #69306

2.1. Модель измерения и основные постулаты метрологии
Для оценки технического состояния технических систем (ТС) в эксплуатации производят измерения ее выходных параметров и на основе измерительной информации принимают решение о при­годности ТС к дальнейшей эксплуатации или необходимости про­филактических (ремонтных) воздействий.

В простейшем случае модель измерения (рис. 2.1) может быть описана функциональной зависимостью изменения выходного сигнала у от изменения входного сигнала х, как у =f(х).


Рис. 2.1. Модель измерения
Однако в процессе измерений возникают различные внешние и внутренние помехи z_i, z_l,.., которые вносят погрешность в результат измерения. Причем каждая из составляющих имеет свою плотность вероятности f (x), f(y), f(z). Это определяет тот факт, что при многократном измерении одной и той же величины х одним и тем же средством измерения в одинаковых условиях результаты измерения, как правило, различаются между собой и не совпадают с истинным х_изначением физической величины

y₁ y₂ … х_и.

Под истинным значением физической величины понимается значение, которое идеальным образом отражало бы в качественном и количественном отношениях соответствующие свойства ТС через ее выходной параметр.

Поскольку истинное значение есть идеальное значение, то в качестве наиболее близкого к нему используют действительное значение х_д,найденное экспериментальным методом, например с помощью более точных СИ.

Изложенное позволяет сформулировать основные постулаты метрологии.

• Истинное значение определяемой величины существует, и оно постоянно.

• Истинное значение измеряемой величины отыскать невоз­можно. Отсюда следует, что результат измерения у, как правило, математически связан с измеряемой величиной вероятностной зависимостью.

В дальнейшем необходимо различать термины "измерение", "контроль", "испытание" и "диагностирование". Контроль — частный случай измерения, и он проводится с целью установления соответствия измеряемой величины заданному допуску. Контроль используется также для настройки, регулировки и при установке (замене) отдельных блоков ТС.

Более сложной метрологической операцией является испытание, которое состоит в воспроизведении в заданной последовательности определенных воздействий, измерении реакций объекта на данное воздействие и регистрации этих реакций.

Диагностированиесистемы — это процесс распознавания состояния элементов этой системы в данный момент времени. По результатам диагностирования можно прогнозировать состояние элементов системы при дальнейшей ее эксплуатации.

Для проведения измерений с целью контроля, диагностирования или испытания ТС необходимо осуществлять мероприятия, определяющие так называемое проектирование измерений: анализ измерительной задачи с выяснением возможных источников погрешностей; выбор показателей точности измерений; выбор числа измерений, метода и СИ; формулирование исходных дан­ных для расчета погрешности" расчет отдельных составляющих и общей погрешности; расчет показателей точности и сопоставле­ние их с выбранными показателями.

В целом все эти вопросы должны быть отражены в методике выполнения измерений (МВИ). Причем следует отдавать предпоч­тение инженерным (упрощенным) методам расчета, но степень сложности МВИ должна быть адекватна возможной степени не­точности исходных данных.

Именно эти вопросы будут рассмотрены ниже. При этом не рассматриваются методы оценки законов распределения измеряемых величин и погрешностей, оценки их достоверности по критериям согласия, выявления аппроксимирующих функций и точности этих аппроксимаций. Данные вопросы достаточно подробно изложены в работах по теории надежности и математической статистике и относятся к исследовательским (лабораторным) ме­тодам измерения [35; 53].
2.2. Виды и методы измерений
Классификация видов измерений приведена на рис. 2.2. Виды измерений определяются физическим характером измеряемой величины, требуемой точностью измерения, необходимой скоростью измерения, условиями и режимом измерений и т. д. Из рис. 2.2 следует, что в метрологии существует множество видов измерений и число их постоянно увеличивается. Можно, например, выделить виды измерений в зависимости от их цели: контрольные, диагностические и прогностические, лабораторные и технические, эталонные и поверочные, абсолютные и относительные и т. д.

Наиболее часто используются прямые измерения, состоящие в том, что искомое значение величины находят из опытных данных путем экспериментального сравнения. Например, длину измеряют непосредственно линейкой, температуру — термометром, силу — динамометром. Уравнение прямого измерения: у= Сх, где С — цена деления СИ.

Если искомое значение величины находят на основании известной зависимости между этой величиной и величинами, найденными прямыми измерениями, то этот вид измерений называют косвенным. Например, объем параллелепипеда находят путем умножения трех линейных величин (длины, ширины и высоты); электрическое сопротивление — путем деления падения напряжения на величину силы электрического тока. Уравнение косвенного измерения у = f(х₁, х₂,..., х_n), где х_i — i-й результат прямого измерения.

Совокупные измерения осуществляются путем одновременного измерения нескольких одноименных величин, при которых искомое значение находят решением системы уравнений, получаемых в результате прямых измерений различных сочетаний этих величин. При определении взаимоиндуктивности катушки М, например, используют два метода: сложения и вычитания полей. Если индуктивность одной из них L₁, а другой — L₂, то находят

L₀₁ = L₁+L₂+2M и L₀₂ = L₁+L₂2M.

Откуда M = (L₀₁  L₀₂)/4.

Совместными называют производимые одновременно (прямые и косвенные) измерения двух или нескольких неодноименных величин. Целью этих измерений, по существу, является нахождение функциональной связи между величинами. Например, измерение сопротивления R_tпроводника при фиксированной температуре tпо формуле

R_t= R₀(1+t),

где R₀ и  — сопротивление при известной температуре t₀(обычно 20 °С) и температурный коэффициент — величины постоянные, измеренные косвенным методом; t = tt₀ — разность температур; t — заданное значение температуры, измеряемое прямым методом.


Рис. 2.2. Классификация видов измерений
Приведенные виды измерений включают различные методы, т. е. способы решения измерительной задачи с теоретическим обоснованием и разработкой использования СИ по принятой МВИ. Методика — это технология выполнения измерений с целью наилучшей реализации метода.

Прямые измерения — основа более сложных измерений, и поэтому целесообразно рассмотреть методы прямых измерений. В соответствии с РМГ 29—99 различают:

1. Метод непосредственной оценки, при котором значение величины определяют непосредственно по отсчетному устройству измерительного прибора, например измерение давления пружинным манометром, массы — на весах, силы электрического тока — амперметром.

2. Метод сравнения с мерой, где измеряемую величину сравнивают с величиной, воспроизводимой мерой. Например, измерение массы на рычажных весах с уравновешиванием гирей; измерение напряжения постоянного тока на компенсаторе сравнением с ЭДС параллельного элемента.

3. Метод дополнения, если значение измеряемой величины дополняется мерой этой же величины с таким расчетом, чтобы на прибор сравнения воздействовала их сумма, равная заранее заданному значению.

4. Дифференциальный метод характеризуется измерением разности между измеряемой величиной и известной величиной, воспроизводимой мерой. Метод позволяет получить результат высокой точности при использовании относительно грубых средств измерения.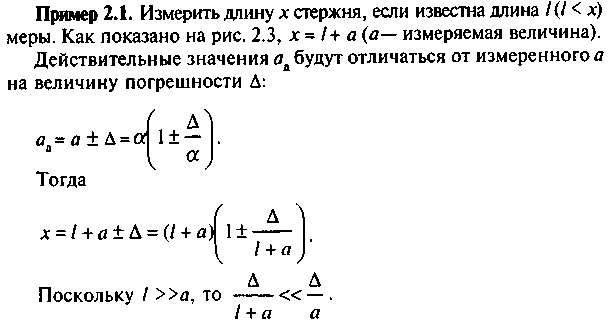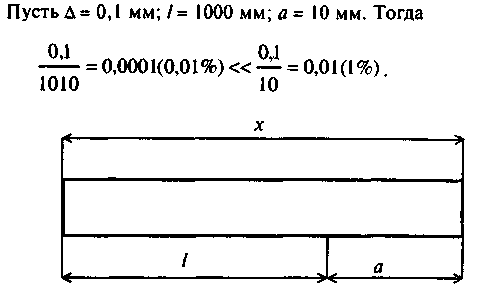




Рис. 2.3. Дифференциальный метод измерения
5. Нулевой метод аналогичен дифференциальному, но разность между измеряемой величиной и мерой сводится к нулю. При этом нулевой метод имеет то преимущество, что мера может быть во много раз меньше измеряемой величины. Рассмотрим, например, неравноплечие весы (рис. 2.4, а), где

Р₁l₁ = Р₂l₂. В электротехнике — это мосты для измерения индуктивности, емкости, сопротивления (рис. 2.4, б). Здесь r₁r₂ = r_xr₃ откуда r_x= r₁r₂/r₃.В общем случае совпадение сравниваемых величин регистрируется нуль-индикатором (И).


Рис. 2.4. Нулевой метод измерения: а — схема механических весов;

б — схема электрического моста
6. Метод замещения — метод сравнения с мерой, в которой измеряемую величину замещают известной величиной, воспроизводимой мерой. Например, взвешивание с поочередным помещением измеряемой массы и гирь на одну и ту же чашку весов.

Кроме того, можно выделить нестандартизованные методы:

• метод противопоставления, при котором измеряемая величина и величина, воспроизводимая мерой, одновременно воздействуют на прибор сравнения. Например, измерения массы на равноплечих весах с помещением измеряемой массы и уравновешивающих ее гирь на двух чашках весов;

• метод совпадений, где разность между сравниваемыми величинами измеряют, используя совпадение отметок шкал или периодических сигналов.

Например, при измерении длины штангенциркулем наблюдают совпадение отметок на шкалах штангенциркуля и нониуса; при измерении частоты вращения стробоскопом — метки на вращающемся объекте с момента вспышек известной частоты.

В литературе [2; 43; 18] иногда встречается название измерений с однократными наблюдениями — обыкновенные измерения, а с многократными — статистические. Кроме того, если весь измеряемый параметр фиксируется непосредственно СИ, то это — абсолютный метод, а если СИ фиксирует лишь отклонение параметра от установочного значения, то это относительный (пороговый) метод измерения.

Другие виды и методы измерений (см. рис. 2.2) не требуют специальных пояснений и будут рассмотрены ниже.