Экзамен мпм. Понятие числа и числа первого десятка. 2. Однозначные числа
 Скачать 274.88 Kb. Скачать 274.88 Kb.
|
|
2. Однозначные числа Числа первого десятка называют однозначными. Они обозначены одной цифрой: 1, 2, 3,4,5,6, 7,8,9. Поскольку число обозначает количественную характеристику множества, его называют количественное натуральное число. (Если мы хотим получить ответ на вопрос: «Сколько?», речь идет о количественном числе.) Фактически при счете элементов множества происходит процесс их нумерации. Счет — это процесс упорядочивания множества путем присвоения каждому элементу определенного номера. Таким образом, понятие числа также неразрывно связано с представлением о порядке, упорядочивании элементов множества. В этом случае натуральное число представляет собой порядковый номер некоторого элемента и называется в силу этого порядковым числом. Количественное и порядковое числа взаимосвязаны, при пересчете элементы конечного множества не только расставляются в определенном порядке, но и устанавливается также, сколько элементов содержит множество (последний порядковый номер, называемый при счете, является характеристикой количества элементов множества). Например: последнее яблоко — пятое, значит их всего пять. Эти две роли натурального числа нашли отражение в русском языке: порядковые натуральные числа выражаются порядковыми числительными (первый, второй, третий..), количественные — количественными числительными (один, два.) Процесс счета подчиняется определенным правилам: первому отмеченному предмету ставится в соответствие число 1 (наименьшее натуральное число); на каждом следующем шаге отмечается (нумеруется) предмет, еще не отмеченный ранее (нельзя считать один и тот же предмет дважды); ему ставится в соответствие число, следующее за последним из уже названных (натуральные числа расположены в строгом равномерном порядке). Данные правила определяют принцип образования чисел в натуральном ряду: каждое следующее число на единицу больше предыдущего. Усвоение ребенком этого принципа является центральной задачей изучения нумерации первого десятка в школе. Следствием этого принципа является идея бесконечности ряда натуральных чисел (как бы ни было велико число, всегда можно найти следующее, добавив к нему единицу), а также способ нахождения значений выражений вида 5 + 1;8+1;6-1;7-1ит. п. путем называния либо следующего, либо предыдущего числа. Иными словами, для нахождения значения данных выражений нет необходимости выполнять какой-то прием арифметических действий, достаточно понимать, что добавление 1 ведет к получению следующего по счету числа, а убавление 1 — означает возврат к предыдущему по счету числу. Именно для получения результатов в таких выражениях ребенок заучивал наизусть названия чисел в прямом и обратном порядке. В умение считать входят: знание слов-числительных, знание («запомненность») порядка их называния при счете, понимание смысла процесса нумерации элементов множества, понимание того, что последний названный номер является характеристикой количественного состава множества, и умение соблюдать правила счета. Большая часть нагрузки при освоении счета приходится на механическую память, т. е. процесс обучения счету в большой мере репродуктивен (опирается на память, а не на мыслительные операции). Для того чтобы ребенок не осваивал его на формальном уровне, на первых порах этот процесс следует обязательно сопровождать предметными действиями: откладыванием, показыванием, а также проговариванием вслух. Следует помнить, что можно предлагать ребенку посчитать двойками, десятками и т. п., но нельзя говорить: «Посчитай от 10 обратно». Процесс счета «векторный», т. е. возможен по определению только в сторону увеличения номеров. Перечисление названий чисел в обратном порядке не является счетом, поскольку слово-числительное, названное при счете последним, является ответом на вопрос «Сколько?», т. е. характеризует количество предметов данной совокупности. Умение называть числительные в обратном порядке является базовым для обучения ребенка процессу отсчитывания, поэтому формировать такое умение необходимо, но формулировать задание следует в виде: «Назови числа в обратном порядке». (Но не «посчитай» Таким же образом формулируются задания: «Назови числа от 6 до 9». (Но не «посчитай от 6 до 9».) 3. Порядок следования чисел в ряду Место числа в ряду определено способом его получения: каждое следующее число становится в ряду справа от предыдущего. Для понимания такого порядка расположения ребенок должен предварительно освоиться с процессом перевода пространственного расположения объектов, подчиненных отношению «следовать за», в плоскость, где отношение «следовать за» подразумевает «ближайшее справа», а «следовать перед» (предшествовать) — ближайшее слева. Число предыдущее — стоит в ряду чисел левее данного. При счете оно называется непосредственно перед данным, количественно содержит на одну единицу меньше данного. Число последующее (следующее) — стоит в ряду чисел правее данного. При счете оно называется непосредственно после данного, количественно содержит на одну единицу больше данного. Так, число пять является предыдущим к числу шесть; число семь является последующим для числа шесть. В первом классе числа пять и семь по отношению к числу шесть часто называют соседями. Так, соседями числа восемь являются числа семь и девять. Хорошее понимание принципа построения натурального ряда чисел ведет в дальнейшем к легкому освоению приемов присчитывания и отсчитывания по 1 и легкому выполнению вычислений в случаях: 7 + 1 17 + 1 177+1 10 277 + 1 7-1 17-1 177-1 10 277 -1 Во всех случаях ссылка на принцип построения натуральной последовательности чисел является наиболее рациональной вплоть до 4 класса (общий прием вычислений): прибавляя к числу 1, получаем следующее по счету; вычитая из числа 1, получаем предыдущее по счету. Этот же прием является действующим и в трудных случаях: 9 + 1 19+1 199 + 1 999+1 99 999 +1 10-1 20-1 200-1 1000 - 1 100 000 -1 При нахождении ответа в данных примерах удобно ссылаться на порядок счета: следующим за числом 99 999 является число 100 000; предшествующим числом для числа 1000 является 999. 4. Состав однозначных чисел Термин «состав однозначных чисел» подразумевает обучение ребенка умению представлять данную количественную совокупность в виде составных частей, обозначая их количественные характеристики словом (числом) или любыми другими символами (числовыми фигурами): Состав числа на числовых фигурах:   Не следует торопиться вводить цифровую символику при изучении состава числа: При раннем введении цифровой символики ребенок механически запоминает пары изображенных цифр, не осознавая количественный смысл соотношения. В дальнейшем это может привести к непониманию смысла закона перестановки слагаемых и неисполь зованию знания состава однозначных чисел при изучении табличных случаев сложения и вычитания в пределах 10. 5.Число О Нуль не считается натуральным числом. При знакомстве с нулем нельзя ссылаться на счет предметов, невозможно выстроить предметную модель нуля. В математике нуль определяют как символ пустого множества. Для обозначения пустого множества используется цифра 0. Число нуль обозначает ситуацию отсутствия предметов, подлежащих счету. Следует правильно формулировать пояснения: - Не осталось ни одной фигуры (предмета), которые мы считали. Для того чтобы это обозначить, используют специальный знак — цифру 0 (нуль, ноль). (В русском языке возможны обе формы.) При этом не стоит говорить: «Ничего нет, значит 0». Нет яблок в корзине (но корзина есть); нет кубиков в коробке; нет листьев на ветке и т. п. Для обозначения того, что яблок в корзине больше нет, используют цифру 0. Вопрос о месте нуля в ряду чисел является важным для правильного формирования представления о натуральном ряде. Не рекомендуется выстраивать последовательность 0, 1,2, 3, 4, 5, 6, 7, 8, 9 в фиксированном виде над доской в классе для того, чтобы она часто попадалась на глаза ребенку. Ребенок фиксирует (запоминает) ряд в таком виде, будучи убежден, что нуль — первое число в ряду, т. е. что нуль — натуральное число. В дальнейшем этот стереотип бывает трудно преодолеть. Например, учителю будет сложно обосновать использование нуля в записи целых десятков: 10, 20, 30... Говорить, что нуль обозначает отсутствие сосчитываемых предметов, здесь нельзя (т. е. «не работает» введенное накануне определение нуля и «не действует» данное при введении нуля обоснование). Для того чтобы объяснить роль нуля в записи двузначного (многозначного) числа необходимо обратиться к понятию «разряд», которое является базовым в десятичной системе счисления. Суть в том, что в записи двузначного (многозначного) числа нуль выполняет роль «сторожа» разрядного места. Поскольку в записи двузначного числа роль цифры зависит от ее позиции (места в записи), одна и та же цифра будет иметь различное значение в зависимости от того, какое место она занимает. Такова структура десятичной системы, и именно поэтому она называется позиционной. Каждая позиция в записи числа имеет свое значение, называемое разрядом. Нуль в записи двузначного числа 10 обозначает, что в первом разряде (разряде единиц) нет значащих цифр, но данная позиция (разряд) в этом числе «задействована», и если к данному числу будут добавляться единицы, то они будут добавляться именно в этот разряд, который пока пуст. 7. Число 10 Десять единиц — это десяток. Десяток является второй счетной единицей в десятичной системе счисления (десятичная система счисления имеет основанием число десять). Десять десятков образуют следующую счетную единицу — сотню. Число 10 является числом, завершающим первый десяток. Число 10 является первым двузначным числом в ряду натуральных чисел. Число 10 является первым целым десятком, с которым знакомится ребенок. В дальнейшем на основе понятия десяток ребенок знакомится с разрядным и десятичным составом двузначных и многозначных чисел. Чтобы не вдаваться в терминологические сложности и не перегружать материал ранним введением понятия «разряд», удобно целиком провести знакомство с десятком и его записью с помощью цифр на предметной модели. Знакомя ребенка с числом 10 (первым двузначным числом и первым целым десятком), очень важно рассмотреть его с различных позиций: и как новое число в ряду (следующее за девятью и потому подчиняющееся общему принципу построения множества натуральных чисел), и как первое число, в записи которого использовано два символа; и как новую счетную единицу (десяток), для чего используют связку десяти палочек в качестве единицы счета: один десяток; два десятка, три десятка... Не следует торопиться вводить стандартные названия этих десятков (двадцать, тридцать.), полезнее один-два урока использовать связки по 10 палочек для счета с целью формирования представления о десятке, как счетной единице. Далее, для того чтобы не начинать процесс знакомства с нумерацией двузначных чисел сложным понятием «разряд», можно провести аналогию способа записи целых десятков с предметной моделью числа. 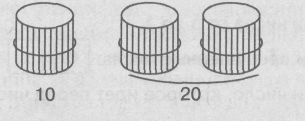 Нуль в такой аналогии символизирует «связку», охватывающее колечко. Для усвоения этой аналогии полезно сразу же предлагать детям и задания обратного вида: покажите на палочках число 30 (три связки), число 40 (четыре связки). Счет десятками (10,20,30,40,50,60,70,80,90) — процесс «технически» аналогичный счету единицами в пределах 10. Полезно научить ребенка присчитывать и отсчитывать десятки так же, как он делал это с единицами. В дальнейшем это умение поможет ребенку легче освоить вычислительные приемы сложения и вычитания в пределах 100. При знакомстве ребенка с нумерацией однозначных чисел рекомендуем педагогу использовать следующие виды заданий: 1) на способ образования каждого следующего числа путем присчитывания единицы к предыдущему: Как из числа 3 получить 4? (Добавить к трем один.) 2) на определение места числа в ряду: За каким числом стоит число 5? (За числом 4.) Где место числа 8? (Между числами 7 и 9.) 3) на сравнение как двух соседних, так и несоседних чисел: Сравните числа: 5...4 У...2 4) на состав числа: 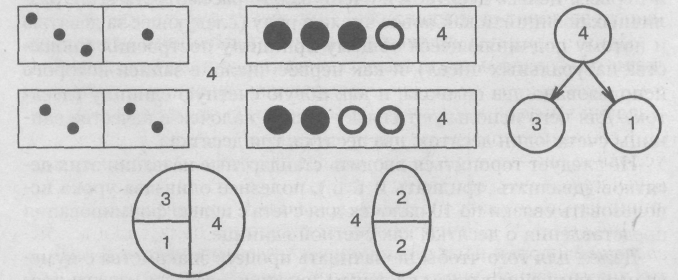 5) на запоминание обратной последовательности числительных в ряду: Назови числа от 5 до 1. Вставь пропущенные числа: Назови число, которое идет перед числом. |
