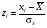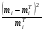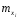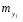Теор вер. 2. Понятие случайного события
 Скачать 396.13 Kb. Скачать 396.13 Kb.
|
|
Проверка: miui2 + 2 miui + mi = mi (ui + 1)2; 268 + 2 · 78 + 100 = 524. Найдем условные характеристики: 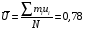 ; ; 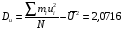 ; ; 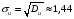 . .Получим характеристики исходного вариационного ряда с использованием равенств xi = hxui + cx: 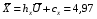 ; Dx = hx2Du = 4,6611; x = hxu = 2,159 ; Dx = hx2Du = 4,6611; x = hxu = 2,1593. По критерию χ2 (Хи-квадрат) проверить гипотезу о нормальном распределении генеральной совокупности при уровне значимости α = 0,05. Решение. Задача проверки статистической гипотезы сводится к тому, чтобы при заданном уровне значимости рассчитать по выборочным данным наблюдаемое значение критерия χ2набл и определить, является ли оно наиболее или наименее правдоподобным в отношении выдвинутой гипотезы. Проверим гипотезу о нормальном распределении генеральной совокупности, используя критерий χ2 (Пирсона) при α = 0,05. В основе этого критерия лежит сравнение частот mi и теоретических частот miT, вычисленных в предположении нормального распределения генеральной совокупности. Критерий χ2 не подтверждает однозначно правильность или неправильность гипотезы, а только устанавливает ее согласие или несогласие с данными выборки при заданном уровне значимости α. В качестве критерия выбирается величина 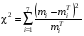 . .Ее значение сравнивают с критическим значением χ2кр, определяемым по соответствующей таблице значений при заданном уровне значимости α и числе степеней свободы k = p– r – 1, где p– число интервалов, r = 2 – число параметров нормального закона распределения (a и ). В данном случаеp= 7, r = 2, k = 7 – 2 – 1 = 4. По таблице распределения случайной величины χ2 с числом степеней свободы k = 4 при уровне значимости α = 0,05 находим χ2кр = 9,49. Если в результате вычислений на основании выборочных данных наблюдаемого значения критерия χ2набл выполняется неравенство χ2набл < χ2кр, то выдвигаемая гипотеза о нормальном распределении генеральной совокупности при заданном α = 0,05 принимается. Если же χ2набл > χ2кр, то гипотезу отвергают. Применим критерий Пирсона к данной выборке. Для этого составим расчетную таблицу, находя теоретические частоты miT для нормального распределения по формуле 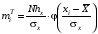 , ,где 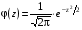 – функция нормального распределения. – функция нормального распределения.
Сумма чисел последнего столбца таблицы дает χ2набл = 1,65. Так как χ2набл = 3,215< χ2кр = 9,49, то гипотеза о нормальном распределении генеральной совокупности принимается. Таким образом, с уровнем значимости α = 0,05 можно считать, что генеральная совокупность распределена по нормальному закону с параметрами a = 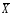 = 4,97, x = 2,159. = 4,97, x = 2,159.Ответ. 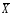 = 4,97; Dx = 4,6611; x = 2,159; гипотеза о нормальном распределении генеральной совокупности принимается. = 4,97; Dx = 4,6611; x = 2,159; гипотеза о нормальном распределении генеральной совокупности принимается.8.2. Построение уравнения прямой регрессии Двумерная выборка результатов совместных измерений признаков x и yобъёмом N= 100 измерений задана корреляционной таблицей (в теле таблицы значения mij – количество раз, когда встретились пары чисел (x, y)):
где 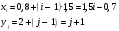 Требуется: 1. Найти 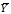 и σy для выборки и σy для выборки
Примечание. Расчёты 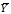 и σy можно выполнить аналогично расчётам и σy можно выполнить аналогично расчётам 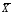 и σx в задаче 8.1 (пункт 2). и σx в задаче 8.1 (пункт 2).2. Построить уравнение прямой регрессии Y на X в виде 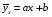 ; ;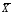 и σx следует взять из задачи 8.1 (пункт 2). и σx следует взять из задачи 8.1 (пункт 2).3. На графике изобразить корреляционное поле, то есть нанести точки (xi,yj) и построить прямую 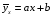 . .Примечание. Уравнение регрессии сначала рекомендуется найти в виде 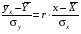 , где r – выборочный коэффициент корреляции, который определяется по формуле: , где r – выборочный коэффициент корреляции, который определяется по формуле: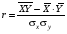 , ,где 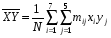 8.2. Построение уравнения прямой регрессии Двумерная выборка результатов совместных измерений признаков x и yобъёмом N= 100 измерений задана корреляционной таблицей (в теле таблицы значения mij – количество раз, когда встретились пары чисел (x, y)):
|