Теор вер. 2. Понятие случайного события
 Скачать 396.13 Kb. Скачать 396.13 Kb.
|
        Тема 1. Элементы комбинаторики: сочетания, размещения, перестановки Тема 1. Элементы комбинаторики: сочетания, размещения, перестановки(нумерация задач выполнена по вариантам с 0 по 9): 4) В ассортименте магазина 10 видов шоколадных конфет. Для составления новогоднего подарка используют 6 видов, причём берется одинаковое количество конфет каждого вида. Сколько различных подарков можно составить? Решение: 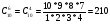 Тема 2. Понятие случайного события. Классическое определение вероятности события 4 вариант Задача 1) Игральная кость подбрасывается один раз. Найти вероятности следующих событий: А1 – выпало 5; А2 – выпало число, кратное трём; А3 – выпало число, меньшее 5. Решение: А1 – выпало 5 (число 5 на игральной кости единственное (одно из шести) 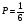 А2 – выпало число, кратное трём (т.е. 3 или 6 (всего 2 числа)) 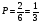 А3 – выпало число, меньшее 5 (т.е. 1,2,3 или 4 (всего 4 числа)) 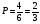 Задача 2) К экзамену приготовлено 24 одинаковых ручки. Известно, что треть из них имеет фиолетовый стержень, остальные - синий стержень. Случайным образом отбирают три ручки. Вычислить вероятность того, что: а) все ручки имеют фиолетовый стержень; б) только одна ручка имеет фиолетовый стержень. Решение: Количество фиолетовых ручек 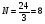 а) все ручки имеют фиолетовый стержень; 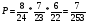 б) только одна ручка имеет фиолетовый стержень. 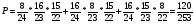 Тема 3. Операции над событиями. Условная вероятность. Теоремы сложения и умножения вероятностей. 4) Один раз подбрасывается игральная кость. События: А – выпало простое число очков; В – выпало четное число очков. Вычислить вероятности Р(А) и Р(А/В). Решение: Простых чисел на игральном кубике 3: 2,3 и 5 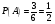 Множество А/В состоит из элементов множества А{2,3,5} без элемента множества В{2}, т.е. А/В{3,5} 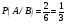 Тема 4. Формула полной вероятности. Формула Бейеса. 4) Партия транзисторов, среди которых 10% дефектных, поступила на проверку. Схема проверки такова, что с вероятностью 0,95 дефект обнаруживается (если он есть), и существует ненулевая вероятность 0,03 того, что исправный транзистор будет признан дефектным. Найти вероятность того, что случайно выбранный из партии транзистор будет признан дефектным. Решение. Рассмотрим гипотезы: Н1 – транзистор выбран из дефектных, Н2 - транзистор выбран из недефектных, Вероятности этих гипотез: 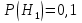 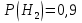 Условные вероятности события A (случайно выбранный из партии транзистор будет признан дефектным) при этих гипотезах равны: 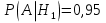 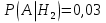 Применяя формулу полной вероятности, получим: 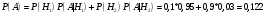 Тема 5. Формула Бернулли. Теорема Пуассона. Локальная и интегральные теоремы Лапласа. 4) Вероятность того, что телевизор имеет скрытые дефекты, равна 0,2. В отдел магазина поступило 20 телевизоров. Что вероятнее: что в этой партии имеется два телевизора со скрытыми дефектами или три? Применим формулу Бернулли 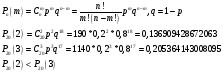 Тема 6. Дискретная случайная величина (ДСВ). Функция и характеристики распределения ДСВ Задан закон распределения ДСВ X(см. ниже варианты заданий). Найти: а) неизвестную вероятность р; б) математическое ожидание М, дисперсию D и среднее квадратическое отклонение случайной величины; в) функцию распределения F(x) и построить её график; г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью y = f(x). 4)
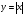 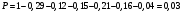 Математическое ожидание 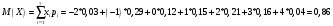 Дисперсия 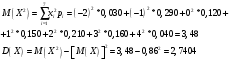 Среднее квадратичное отклонение 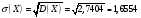 Функция распределения 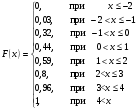 г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью 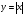 . .4)
или, сложив вероятности при одинаковых значениях х
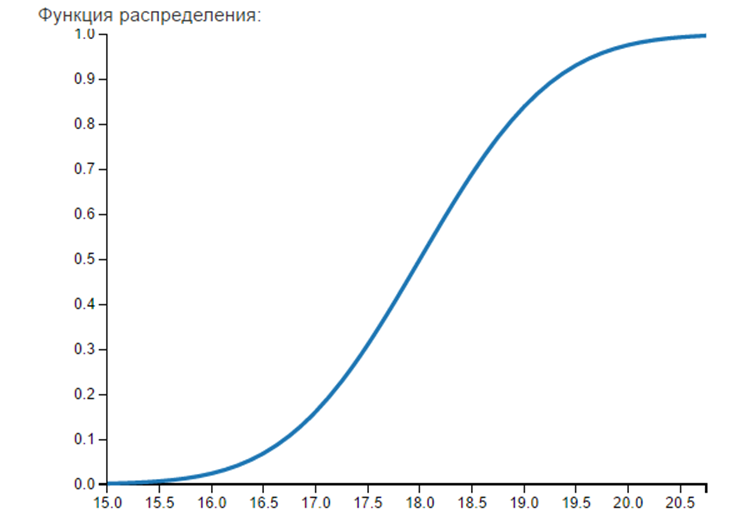
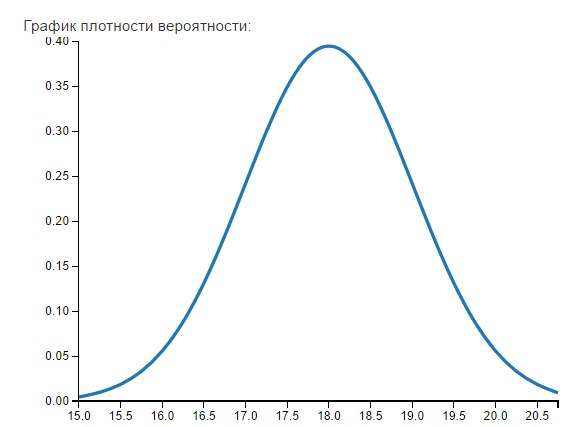
Тема 7. Непрерывная случайная величина (НСВ). Функция распределения и плотность вероятности НСВ НСВ Х имеет нормальное распределение с математическим ожиданием Mx и средним квадратичным отклонением σx. Найти для заданных значений Mx, σx,a, b (см. ниже таблицу вариантов):
Варианты заданий по теме 7
Вероятность того, что 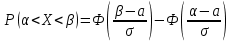 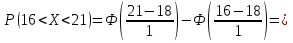 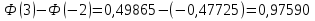
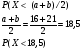 Применим формулу 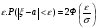 Подставляя значения получим 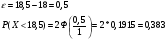
Правило трёх сигм - практически все значения нормально распределённой случайной величины лежат в интервале 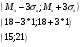
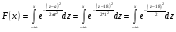  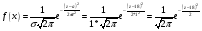 
квантиль x0,7 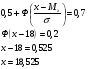 20%-я точка, это квантиль x0,8 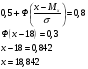 Тема 8. Математическая статистика
8.1. Численная обработка данных одномерной выборки ВыборкаX объёмом N= 100 измерений задана таблицей:
где xi – результаты измерений, 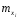 – частоты, с которыми встречаются значения xi, – частоты, с которыми встречаются значения xi, 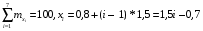 Требуется: 1. Построить полигон относительных частот 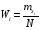 . .2. Вычислить среднее выборочное 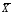 , выборочную дисперсию Dxи среднее квадратическое отклонение σx. , выборочную дисперсию Dxи среднее квадратическое отклонение σx.3. По критерию χ2 проверить гипотезу о нормальном распределении генеральной совокупности при уровне значимости α = 0,05. Примечание. Для расчётов 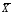 и Dx рекомендуется перейти к условным значениям и Dx рекомендуется перейти к условным значениям 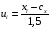 и, взяв за ложный нуль сx значение с наибольшей частотой, использовать суммы и, взяв за ложный нуль сx значение с наибольшей частотой, использовать суммы 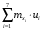 и и 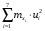 . .Решение задачи 8.1. (обработка данных одномерной выборки) ВыборкаX объёмом N= 100 измерений задана таблицей:
где xi – результаты измерений, 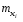 – частоты, с которыми встречаются значения xi. – частоты, с которыми встречаются значения xi.1. Построим полигон относительных частот 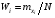 . .Решение. Вычислим относительные частоты 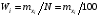 : :
Построим полигон относительных частот: 2. Вычислить среднее выборочное 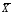 , выборочную дисперсию Dxи среднее квадратическое отклонение σx. , выборочную дисперсию Dxи среднее квадратическое отклонение σx.Решение. Для вычисления 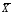 , Dxи σx воспользуемся методом произведений. Введем условные варианты: , Dxи σx воспользуемся методом произведений. Введем условные варианты: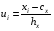 , ,где cx – значение xi, которому соответствует наибольшая частота, cx = x3 = 3,8 (max mi = m4 = 29), шаг выборки hx = 1,5. Тогда, вычисляя ui, получим условный ряд:
Для этого ряда составим расчетную таблицу:
|