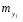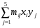Теор вер. 2. Понятие случайного события
 Скачать 396.13 Kb. Скачать 396.13 Kb.
|
|
где 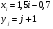 Решение задачи 8.2. (построение уравнения прямой регрессии) Двумерная выборка результатов совместных измерений признаков x и yобъёмом N= 100 измерений задана корреляционной таблицей:
1. Найти 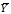 и σy для выборки и σy для выборки
Решение. Для вычисления 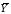 , Dyи σy воспользуемся методом произведений. Введем условные варианты: , Dyи σy воспользуемся методом произведений. Введем условные варианты: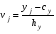 , ,где cy – значение yj, которому соответствует наибольшая частота, cy = y3 = 4 (max mj = m3 = 43), шаг выборки hy = 1. Тогда, вычисляя vj, получим условный ряд:
Для этого ряда составим расчетную таблицу:
Проверка: mjvj 2 + 2mjvj + mj = mj(vj + 1)2; 81 + 2 · (-1)+ 100 = 179 Найдем условные характеристики: 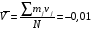 ; ; 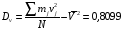 ; ; 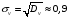 . .Получим характеристики исходного вариационного ряда с использованием равенств yj = hyvj + cy: 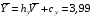 ; Dy = hy2Dv = 0,8099; y = hyv = 0,9 ; Dy = hy2Dv = 0,8099; y = hyv = 0,92. Построить уравнение прямой регрессии Y на X в виде 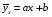 . .Решение. Уравнение прямой регрессии Y на X имеет вид: 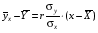 . .Значения xi и частоты их появления 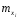 совпадают с данными для задачи 8.1. совпадают с данными для задачи 8.1. Следовательно, 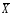 = 4,97; x = 2,159; = 4,97; x = 2,159; 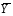 = 3,99; y = 0,9. = 3,99; y = 0,9.Коэффициент корреляции определяется по формуле: 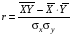 , где , где 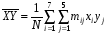 . .Для нахождения 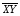 воспользуемся корреляционной таблицей воспользуемся корреляционной таблицей
Из таблицы следует, что 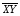 = 2135,7/ 100 =2,1357 = 2135,7/ 100 =2,1357Таким образом, 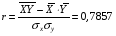 . .. Уравнение прямой регрессии Y на X имеет вид: 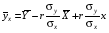 = 2,363 + 0,327x = 2,363 + 0,327x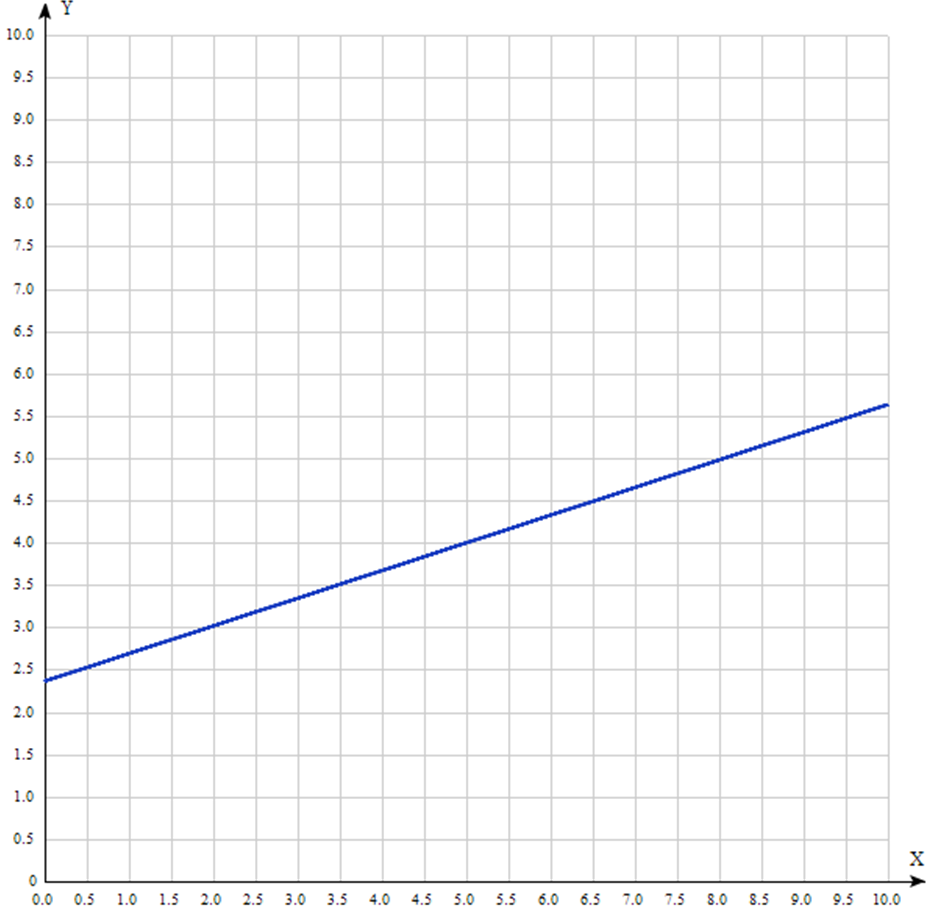 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||