Вариант. вар. 2. Прямоугольный параллелепипед описан около сферы радиуса Найдите его площадь поверхности
 Скачать 111.34 Kb.
|
|
1. 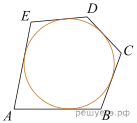 Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.2.  Прямоугольный параллелепипед описан около сферы радиуса 1. Найдите его площадь поверхности.3. У Вити в копилке лежит 12 рублёвых, 6 двухрублёвых, 4 пятирублёвых и 3 десятирублёвых монеты. Витя наугад достаёт из копилки одну монету. Найдите вероятность того, что оставшаяся в копилке сумма составит более 70 рублей. 4. Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4. 5. Решите уравнение  Если уравнение имеет более одного корня, в ответе запишите больший из корней.6. Найдите значение выражения  если  а  7. На рисунке изображен график производной функции f(x), определенной на интервале (−2; 12). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.  8. Расстояние (в км) от наблюдателя, находящегося на высоте h м над землeй, выраженное в километрах, до наблюдаемой им линии горизонта вычисляется по формуле  где  км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 6,4 километров?9. Бригада маляров красит забор длиной 240 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 60 метров забора. Определите, сколько дней бригада маляров красила весь забор. 10.  На рисунке изображены графики функций  и  которые пересекаются в точках A и B. Найдите ординату точки B.11. Найдите наибольшее значение функции  12. а) Решите уравнение  б) Укажите корни этого уравнения, принадлежащие отрезку  13. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A, B и C, а на окружности другого основания — точка C1, причём CC1 — образующая цилиндра, а AC — диаметр основания. Известно,что   а) Докажите, что угол между прямыми  и BC равен  б) Найдите объём цилиндра. 14. Решите неравенство  15. 15-го января планируется взять кредит в банке на сумму 2,4 млн рублей на 24 месяца. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца; — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Какую сумму нужно выплатить банку в первые 12 месяцев? 16. Дана трапеция с диагоналями равными 8 и 15. Сумма оснований равна 17. а) Докажите, что диагонали перпендикулярны. б) Найдите площадь трапеции. 17. Найдите все значения a, при каждом из которых наибольшее значение функции  не меньше 1.18. На конкурсе «Мисс−261» выступление каждой участницы оценивают шесть судей. Каждый судья выставляет оценку — целое число баллов от 0 до 10 включительно. Известно, что за выступление участницы С все члены жюри выставили различные оценки. По старой системе оценивания итоговый балл за выступление определяется как среднее арифметическое всех оценок судей. По новой системе оценивания итоговый балл вычисляется следующим образом: отбрасываются две наибольшие оценки, и считается среднее арифметическое четырех оставшихся оценок. а) Может ли разность итоговых баллов, вычисленных по старой и новой системам оценивания, быть равной 18? б) Может ли разность итоговых баллов, вычисленных по старой и новой системам оценивания, быть равной  в) Найдите наименьшее возможное значение разности итоговых баллов, вычисленных по старой и новой системам оценивания. |