Стоимость денежных потоков-консп. лек. Стоимость денежных потоков-консп. 2. Стоимость денежных потоков. Приведенная и будущая стоимость
 Скачать 0.64 Mb. Скачать 0.64 Mb.
|
|
2. Стоимость денежных потоков. 2.1. Приведенная и будущая стоимость. Наращенная сумма, полученная в результате потока платежей, называется будущей стоимостью FV (future value). Начальная стоимость потока платежей называется приведенной стоимостью PV (present value). В предыдущей главе процессы наращения и дисконтирования рассматривались при осуществлении разового платежа в определенное время. На практике погашение долгосрочной банковской ссуды, коммерческого кредита, арендные платежи, страховые платежи, погашение ипотечного кредита, инвестиции и т.д. предполагают выплаты или денежные поступления через определенные промежутки времени. Возникает распределенный во времени денежный поток (cash flows stream), причем в общем случае неодинаковыми по величине разовыми платежами и с разными процентными ставками за периоды. Наращенную сумму, полученную в результате потока платежей, будем называть будущей стоимостью и обозначать, как это принято в большей части финансовой литературы FV (future value). Начальную стоимость потока платежей будем, как это принято, называть приведенной стоимостью и обозначать PV (present value). Существуют потоки платежей, которые поступают через равные промежутки времени, члены потока либо положительны (доход), либо отрицательны (выплаты), либо подчинятся какому-то определенному закону. Возможны и такие потоки платежей, которые поступают в разные промежутки времени и могут быть, как положительными, так и отрицательными разными по величине. Для наглядности принято графическое изображение потоков платежей. Такое представление позволяет решать достаточно сложные задачи, связанные с распределенными во времени потоков платежей. Рис. 2.1. Графическое изображение будущей стоимости потока платежей. 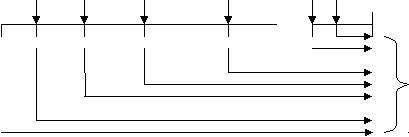  0 1 2 3 i N 0 1 2 3 i NFV Будущая стоимость такого потока платежей будет равна сумме стоимостей наращенных потоков платежей. где где N – число периодов начисления. Величина Пусть теперь имеется поток платежей, показанный на рис.2. Рис.2.2. Графическое изображение приведенной стоимости потока платежей. 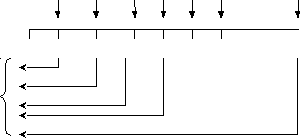 C1 C2 C3 C4 C5 Ci CN C1 C2 C3 C4 C5 Ci CN 0 1 2 3 4 5 i N Приведенная стоимость такого потока равна сумме дисконтированных стоимостей платежей. 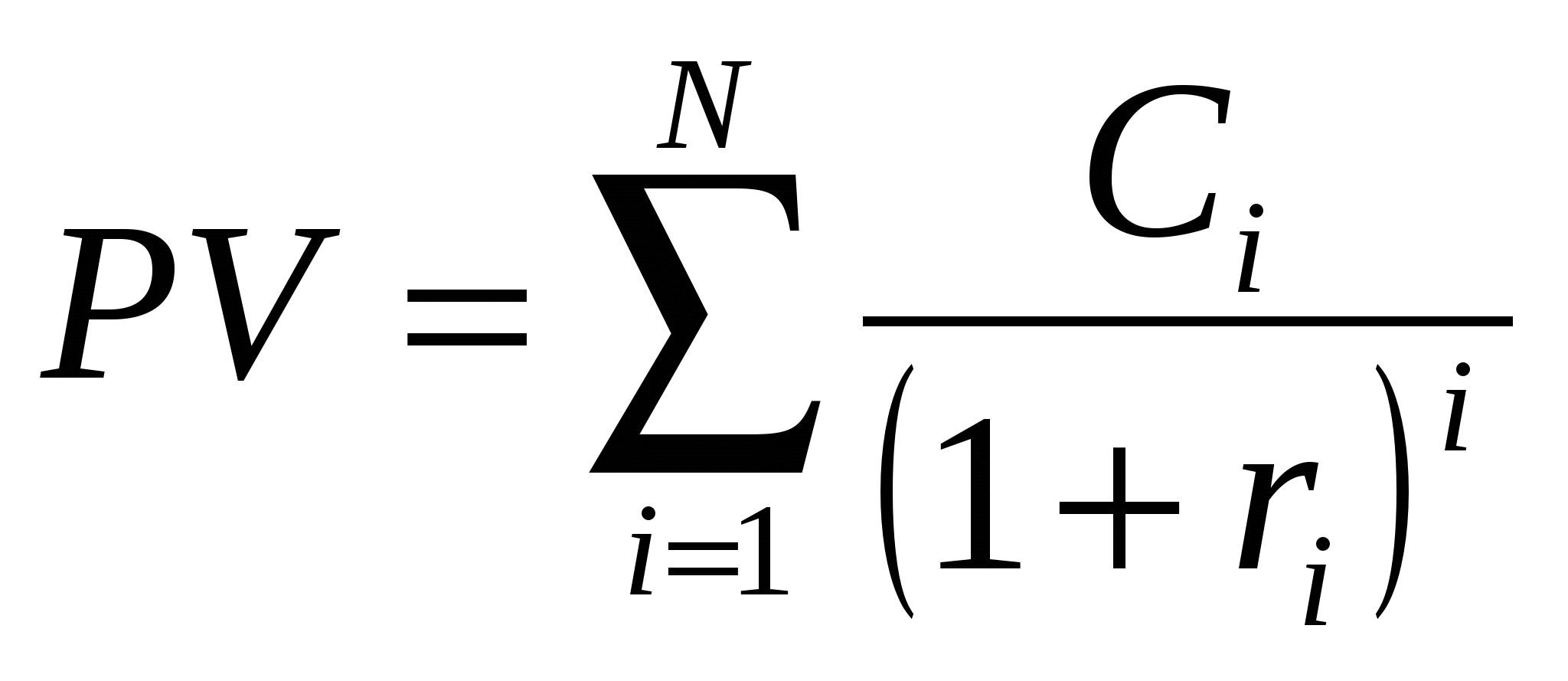 , (2.3) , (2.3)где Величина Задачи, в которых необходимо находить приведенную и будущую стоимость потоков платежей, очень разнообразны. Это ренты, страховки, кредиты, ипотека, оценка инвестиций и т.д. Доходность денежного потока. Представим на графике зависимость приведенной стоимости от процентной ставки. Для потока платежей, рассмотренного выше, эта зависимость имеет вид показанный на рисунке ниже. Рис.2.5 Зависимость чистой приведенной стоимости от величины процентной ставки. 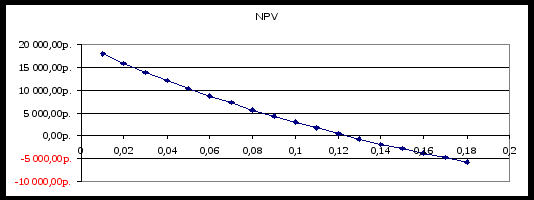 Из графика видно, что существует такая процентная ставка, при которой PV равна нулю. При этой процентной ставке приведенные стоимости затрат и доходов равны. Такая процентная ставка называется внутренней ставкой доходности (внутренней доходностью потока платежей) – «ВСД» (IRR – internal rate of return). Внутренняя ставка доходности применяется для оценки доходности инвестиции. 2.2. Основные параметры и типы рент. Наиболее часто на практике встречаются регулярные и постоянные по величине денежные потоки. Например: арендные платежи, страховые платежи, платежи по кредитам и др. Если имеется денежный поток с равными поступлениями через равные промежутки времени и постоянной процентной ставкой, то такой поток называют аннуитетом2 или простой финансовой рентой. Кроме простых рент существуют и другие типы рент. Например, возрастающие или убывающие. Однако для всех типов рент сохраняется принцип регулярности платежей. Финансовая рента (далее просто рента), характеризуется следующим набором параметров:
стоимость ренты;(?) процентная ставка. Обычно при заключении договора ренты указываются годовые процентные ставки, тогда процентная ставка за период равна частному от деления годовой процентной ставки на число периодов в году. В зависимости от конкретных условий существует много типов рент. Финансовые ренты различаются не только по моментам платежа (обыкновенные и авансовые), длительности (срочная и бессрочная), но также по частоте платежей и начислений процентов и по моменту начала ренты (отложенная рента). Существуют ренты, расчет которых ведется по простым процентам, а также смешанные и переменные ренты. Ренты также различаются по моментам расчета приведенной и будущей стоимости. Обыкновенная рента. Обыкновенная рента (постнумерандо). Приведенная стоимость ренты рассчитывается за период до первой выплаты. Будущая стоимость рассчитывается в момент последней выплаты. Обыкновенная рента (постнумерандо). Приведенная стоимость ренты рассчитывается за период до первой выплаты. Будущая стоимость рассчитывается в момент последней выплаты. Рис.2.1. Моменты расчета приведенной и будущей стоимостей обыкновенной ренты. 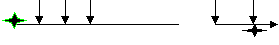 PV PV0 1 2 3 N FV Звездочкой отмечены моменты расчета соответственно будущей и приведенной стоимости. Будущая стоимость обычной ренты рассчитывается в момент последней выплаты и по формуле (2.2) равна На первый взнос наращение производится в течении (N - 1) периодов, а на последний взнос проценты не начисляются. Приведенная стоимость обычной ренты рассчитывается за период до первой выплаты и по формуле (2.3) равна N – число периодов ренты. Авансовая рента. Авансовая рента (пренумерандо). Приведенная стоимость ренты рассчитывается на момент первой выплаты. Будущая стоимость рассчитывается через период после последней выплаты. Распределение потов платежей в авансовой ренте показано на рис.2.2. Рис.2.2. Моменты расчета приведенной и будущей стоимостей авансовой ренты.  PV PV0 1 2 N FV Звездочкой отмечены моменты расчета соответственно будущей и приведенной стоимости. Будущая стоимость рассчитывается через период после последней выплаты и равна Приведенная стоимость авансовой ренты рассчитывается на момент первой выплаты и по формуле (2.3, 2.4) равна Первый платеж не дисконтируется. Нетрудно получить связь между приведенной стоимостью обыкновенной и авансовой рентой. Сравнивая формулы (2.7) и (2.9) получим Если денежные поступления продолжаются достаточно длительное время обычно около 30 лет, то такая рента называется бессрочной (perpetuity). К бессрочным рентам относятся невыкупаемые облигации, приносящие постоянный доход, некоторые виды страховых платежей. Приведенная стоимость бессрочной ренты равна Эта формула легко получается из (2.4). Действительно, при очень больших N величина  В формулах (2.1) – (2.11) подразумевается процентная ставка за период. Для годовой ренты ставка за период – это годовая процентная ставка. Для годовой ренты с начислением 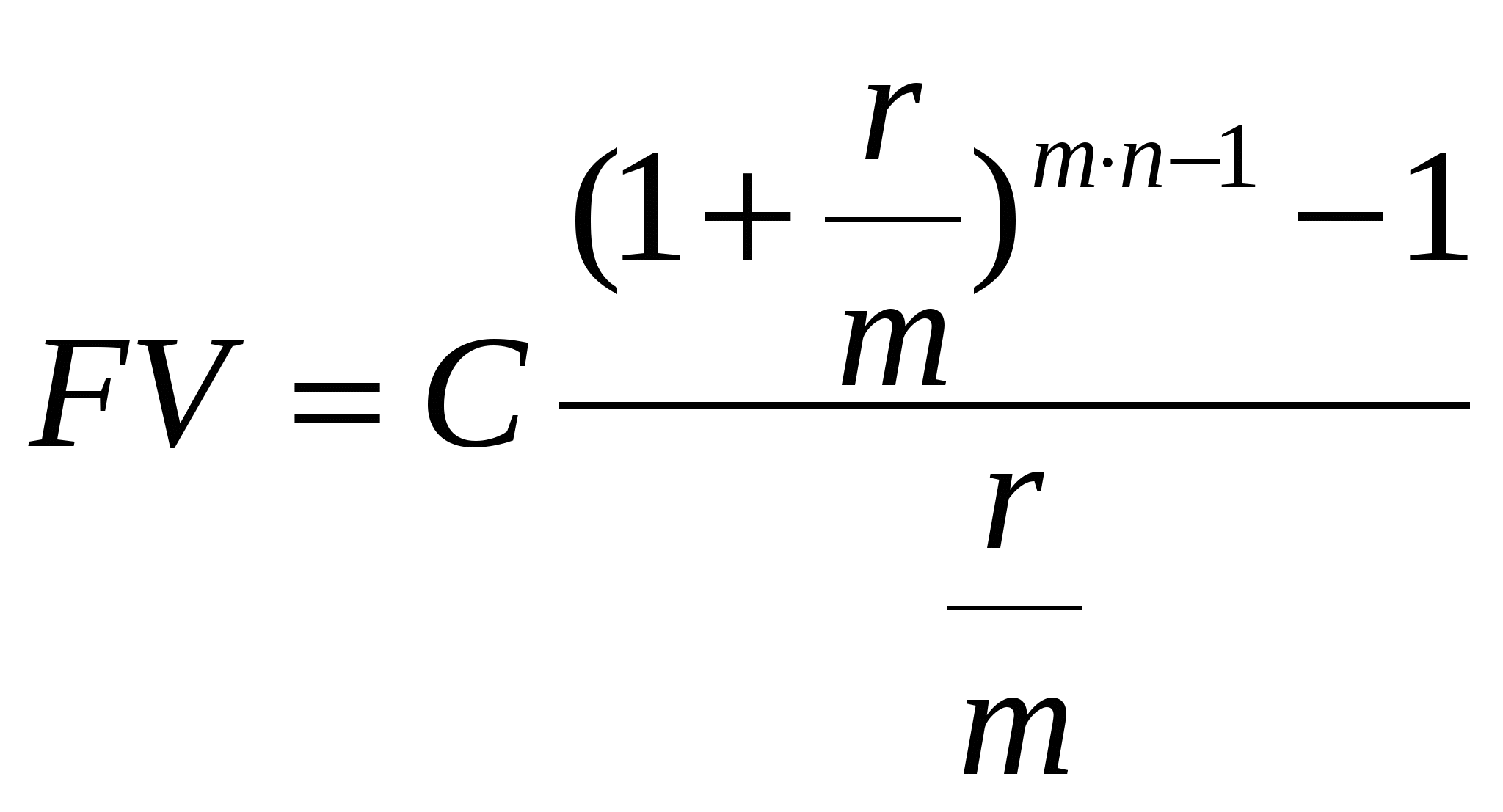 (2.12) (2.12)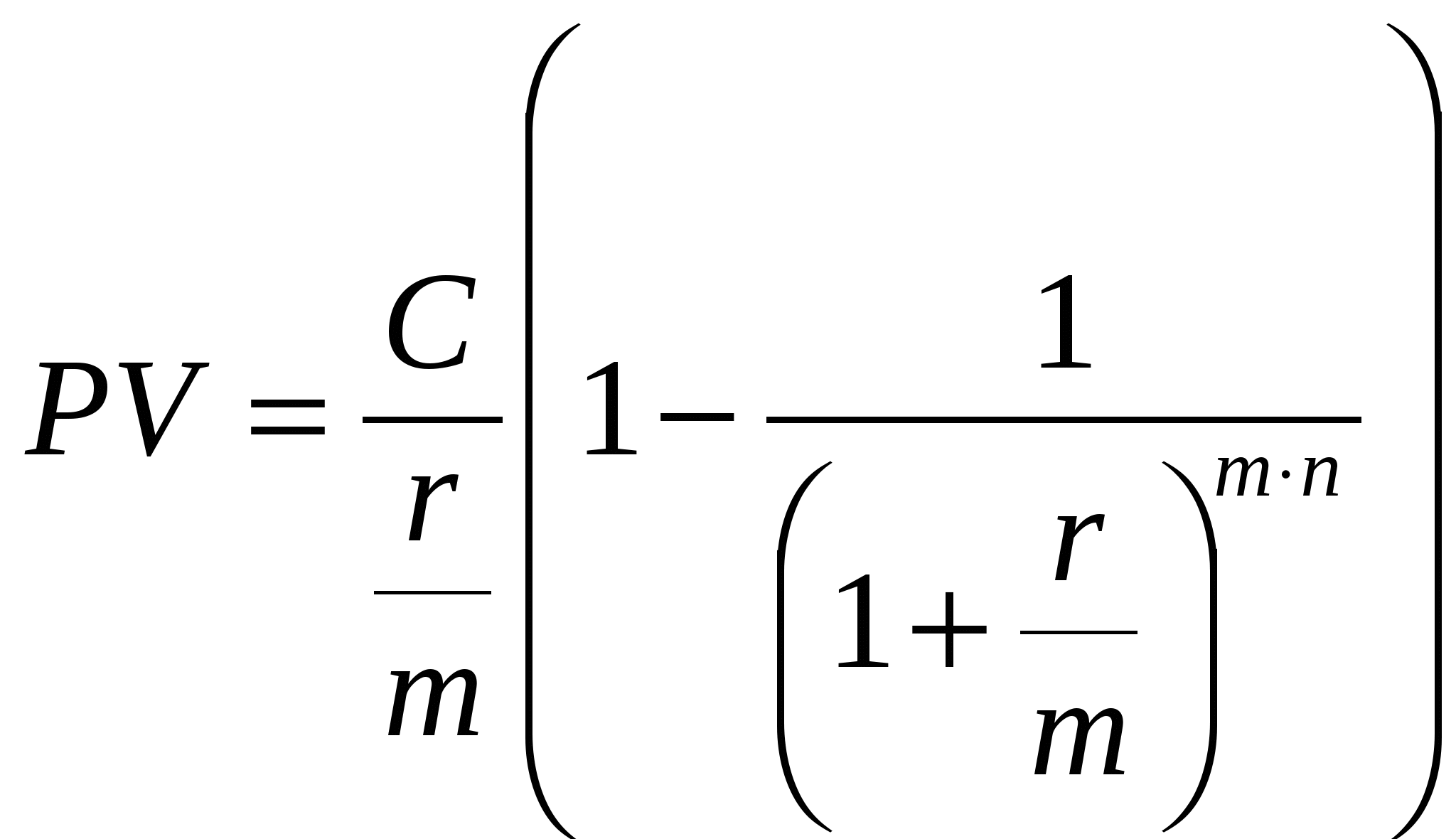 (2.13) (2.13)Основные типы накопительных пенсионных программ. В исследовании Всемирного банка, посвященном проблемам финансового обеспечения лиц пенсионного возраста, делается вывод, что наилучшим образом интересы финансового обеспечения пенсионеров и экономического роста государства обеспечиваются, если развиваются трехуровневые пенсионные системы. Первый уровень - управляемая государством распределительная система, предусматривающая обязательное участие всех лиц, достигших пенсионного возраста и преследующая ограниченную цель: сокращения нищеты среди престарелых. Это так называемая страховая пенсия4. Выплаты четко определенных пособий финансируются за счет поступлений от налогообложения фонда заработной платы. Второй уровень - находящаяся в частном управлении обязательная накопительная система. Третий уровень - добровольная накопительная система. Последние два уровня реализуется посредством заключения договора с некоторым негосударственным пенсионным фондом (НПФ), который управляет пенсионными накоплениями. При этом деятельность этих фондов регламентируется соответствующими законами со стороны государства. При расчетах размеров выплат и платежей НПФ необходимо также учитывать доходность операций по размещению активов НПФ. В связи с этим возникает проблема прогнозирования на несколько лет уровня доходности операций по размещению активов фонда. В договоре с НФП могут быть предусмотрены дополнительные условия. Например, индексация пенсионных выплат, возвраты взносов и инвестиционного дохода участнику или его наследникам. Существуют две основные схемы, реализуемых НПФ. В пенсионной схеме с фиксированными взносами работодатель или сам участник пенсионной схемы делает взносы, составляющие некоторую долю заработной платы. При этом не гарантируется уровень величины пенсионных выплат. Эта величина зависит от накоплений, следовательно, от качества управления фондом. Весь риск будущей величины пенсии участник берет на себя. В пенсионной схеме с фиксированными выплатами участник получает постоянные выплаты после наступления пенсионного срока в течении определенного промежутка времени. Весь риск по обеспечению фиксированных выплат согласно договору берет на себя пенсионный фонд. Пример 10. Пусть Петр Данилов выбрал пенсионный фонд с фиксированным пособием. Он желает получать в течении 15 лет после выхода на пенсию дополнительную пенсию в размере 3000 руб. ежемесячно. Пусть процентная ставка на этот период постоянна и равна 10%. Данилову до пенсии 20 лет. Сколько надо вносить ежемесячно в пенсионный фонд, чтобы получать дополнительную пенсию? Доходность пенсионного фонда на этот период равна 8% годовых. Решение. Графически структура платежей имеет вид 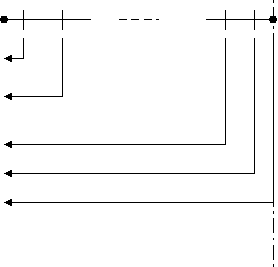   So So So So So S S Vo Vo Vo V So So So So So S S Vo Vo Vo V0 1 2 (n-1) n 0 1 2 So(1+r0) Vo/(1+r1)2 So(1+r0)2 Vo/(1+r1)m-2 So(1+r0)n-2 So(1+r0)n-1 Vo/(1+r1)m So(1+r0)n |
