огдодщощшозщощзогзщ. 2. Вычислите определенные интегралы
 Скачать 25.79 Kb. Скачать 25.79 Kb.
|
|
2. Вычислите определенные интегралы 1) 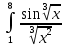 Пусть u = 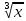 , тогда du = , тогда du = 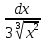 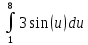 = -3cos (u = -3cos (u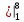 = -3cos ( = -3cos (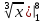 = -3 cos (2) + 3 cos (1) = 3 cos (1) – 3 cos (2) = -3 cos (2) + 3 cos (1) = 3 cos (1) – 3 cos (2)2) 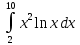 Пусть u = ln x, тогда du = 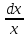 , ,dv = 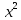 , тогда v = , тогда v = 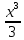 ln x * 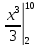 - - 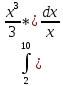 = = 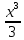 ln x - ln x - 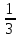 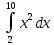 = = 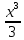 ln x - ln x -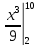 = = 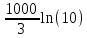 - - 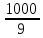 – ( – (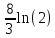 - - 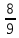 ) = ) = 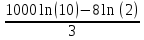 - - 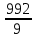 = = 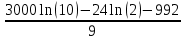 3. Удовлетворяет ли заданная функция данному уравнению Z = 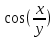 , , 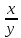 * * 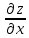 + + 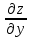 = 0 = 0Найдем частные производные 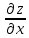 и и 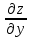 : :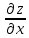 = - = -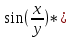 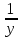 = - = - 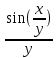 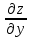 = =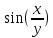 * *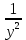 = = 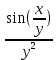 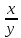 * * 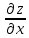 + + 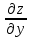 = 0 = 0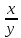 * * 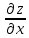 = - = - 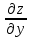 Подставим частные производные в уравнение и проверим равенство: 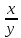 *(- *(- 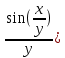 = - = - 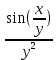 - 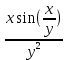 ≠ - ≠ - 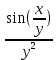 , значит, заданная функция не удовлетворяет данному уравнению , значит, заданная функция не удовлетворяет данному уравнению4. Вычислите двойной интеграл по области D, ограниченной указанными линиями: ∫ 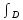 2x dx dyD: x+y = 3, х = 2x dx dyD: x+y = 3, х = 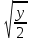 , х = 0 , х = 05. Решите дифференциальные уравнения: 1) 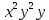 ' + 1 = y ' + 1 = y2) 6. Запишите формулу общего члена ряда 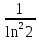 + + 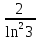 + + 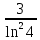 + + 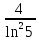 + … + …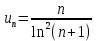 7. Пользуясь необходимым признаком сходимости, докажите расходимость ряда 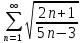 , ,Согласно необходимому признаку сходимости ряда, если ряд 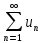 расходится, то расходится, то 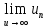  0. 0.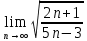 = = 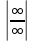 = = 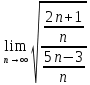 = = 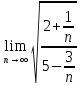 = = 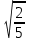  0 0Следовательно, ряд 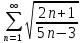 расходится расходится8. Исследовать ряд 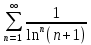 на сходимость, применяя какой-либо из достаточных признаков сходимости на сходимость, применяя какой-либо из достаточных признаков сходимостиВоспользуемся радикальным признаком Коши: Пусть 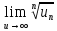 = p, то при p < 1 ряд сходится, при p > 1 ряд расходится = p, то при p < 1 ряд сходится, при p > 1 ряд расходится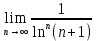 = = 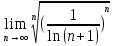 = = 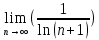 = 0 < 1 = 0 < 1Значит, ряд 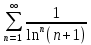 сходится сходится9. Записать ряд 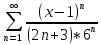 в развернутом виде. Найти его интервал сходимости. Исследовать сходимость ряда на концах найденного интервала в развернутом виде. Найти его интервал сходимости. Исследовать сходимость ряда на концах найденного интервалаЗапишем ряд в развернутом виде: 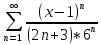 = = 10. Разложить функцию в ряд Тейлора: r(x) = 1/x по степеням (х+2) Воспользуемся формулой Тейлора: f(x) = f( 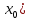 + + 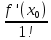 (x- (x-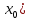 + + 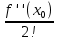 + + 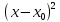 + … + + … + 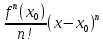 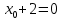 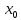 = - 2 = - 2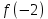 = - = -  Найдем производные функции и ее значения при 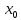 = - 2: = - 2: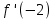 = - = - 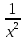 при x = - 2 при x = - 2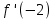 = - = - 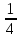 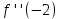 = = 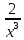 при x = - 2 при x = - 2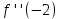 = - = - 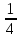 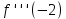 = - = - 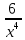 при x = - 2 при x = - 2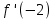 = - = - 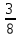 Таким образом, получим: 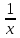 = - = -  + + 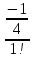 (x+2 (x+2 + + 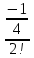 + + 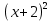 + + 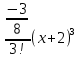 +… +… 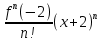 |
