Ответы к экзамену по физике 1 курс. 2 закон Ньютона F ma (докво)

Название	2 закон Ньютона F ma (докво)
Анкор	Ответы к экзамену по физике 1 курс.docx
Дата	18.01.2018
Размер	35.3 Mb.
Формат файла
Имя файла	Ответы к экзамену по физике 1 курс.docx
Тип	Закон #14457
страница	4 из 5

1 2 3 4 5

Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо силотносительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Пренебрегая сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести записывается следующим образом:

$i\frac{d^2\theta}{dt^2} = -mgh\sin\theta$ .

гармонический осциллятор — это система, уравнение движения которой описывается дифференциальным уравнением 2 x + ω0 x = 0, ¨ (1) где x — величина, совершающая колебания, ω0 — циклическая частота.
При механических колебаниях колеблющееся тело (или материальная точка) обладает кинетической и потенциальной энергией.Кинетическая энергия тела W:

(Скорость тела v = ds/dt)

Для вычисления потенциальной энергии тела воспользуемся самой общей формулой, связывающей силу и потенциальную энергию тела в поле этой силы: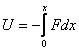

где U - потенциальная энергия, набираемая (или теряемая) телом, движущимся в силовом поле F от точки 0 (точки, в которой потенциальная энергия принимается равной 0) до точки х.

Для силы, линейно зависящей от смещения (как в случае наших механических маятников, такие силы носят общее название квазиупругих сил) мы имеем:

;

Сравнивая формулы для кинетической и потенциальной энергии, можно сделать выводы:
1. Полная механическая энергия тела не изменяется при колебаниях:

2. Частота колебаний кинетической и потенциальной энергии в 2 раза больше частоты колебаний маятника.
3. Колебания кинетической и потенциальной энергии сдвинуты друг относительно друга по фазе на  (на полпериода). Когда кинетическая энергия достигает максимума, потенциальная - минимума (нуля) и наоборот. Энергия при колебаниях постоянно перекачивается из потенциальной в кинетическую и обратно.

3.4 Упругие (механические) волны. Механизмы и условия возникновения упругих волн. Поперечные и продольные упругие волны, условия их возникновения. Формула скорости упругих волн в различных средах. Длина волны. Циклическое волновое число. Уравнение плоской волны.

Механической волной называется процесс распространения колебаний в упругой среде, который сопровождается передачей энергии от одной точки среды к другой.

Источником механической волны является колеблющее тело. Если источник колеблется синусоидально, то и волна в упругой среде будет иметь форму синусоиды. Колебания, вызванные в каком-либо месте упругой среды, распространяются в среде с определенной скоростью, зависящей от плотности и упругих свойств среды.

Подчеркнем, что при распространении волны отсутствует перенос вещества, т. е. частицы только колеблются вблизи положений равновесия.

Различают продольные и поперечные волны.

Упругая волна называется продольной, если частицы среды колеблются в направлении распространения волны. Продольные волны связаны с объемной деформацией упругой среды и потому могут распространяться в любой среде — твердой, жидкой и газообразной. Примером таких волн являются звуковые волны в воздухе.

Упругая волна называется поперечной, если частицы среды колеблются, оставаясь в плоскостях, перпендикулярных направлению распространения волны. Поперечные волны связаны с деформацией сдвига упругой среды и, следовательно, могут образовываться и распространяться только в средах, обладающих упругостью формы, т. е. в твердых телах. Примером поперечных волн могут, служить волны, распространяющиеся вдоль струн музыкальных инструментов.

Фазовая скорость различна для разных сред. В случае упругих поперечных волн (в твердом теле) фазовая скорость равна: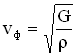

,где

- модуль сдвига среды,

-ее плотность в невозбужденном состоянии (т.е. когда в этой среде не распространяется упругая волна).

Фазовая скорость упругих продольных волн в твердом теле равна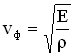

,

где Е - модуль Юнга,

- плотность невозмущенной среды (твердого тела до момента распространения по нему волны).

Фазовая скорость продольных волн в жидкости и газе определяется соотношением: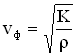

,где К – модуль объемной упругости среды– величина, характеризующая способность среды сопротивляться изменению ее объема,

- плотность невозмущенной среды.

Фазовая скорость продольных волн в идеальном газе задается формулой: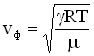

- показатель адиабаты,

- молярная масса, Т – абсолютная температура, R – универсальная газовая постоянная. Фазовая скорость в газе зависит от сорта газа (

) и от его термодинамического состояния (Т).

Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками, колеблющимися в одинаковых фазах, обычно длина волны обозначается греческой буквой $\lambda$ . По аналогии с возникающими волнами в воде от брошенного в неё камня — расстояние между двумя соседними гребнями волны. Одна из основных характеристикколебаний. Измеряется в единицах расстояния (метры, сантиметры и т. п.). Величина $k=\frac{2\pi}{\lambda}$ , обратная длине волны, называется волновым числом и имеет смысл пространственной частоты.

Получить соотношение, связывающее длину волны с фазовой скоростью (

) ичастотой(

) можно из определения. Длина волны соответствует пространственному периоду волны, то есть расстоянию, которое точка с постоянной фазой проходит за время, равное периоду колебаний

, поэтому

$\lambda = vt = \frac{v}{f} = \frac{2\pi v}{\omega}$

Уравнение плоской волны:
Волна называется плоской , если ее волновые поверхности представляют совокупность плоскостей, параллельных друг другу. В плоской волне , распространяющейся вдоль оси ОХ , все величины s, характеризующие колебательные движение среды, зависят только от времени и координаты х точки М среды. Колебания происходят по закону s=f(t), но сдвинуты во времени на x\v. Поэтому ур-ие плоской волны имеет вид: s=f(t-x\v). Синусоидальная волна:

s=Asin(wt-wx\v+j₀). A=const – амплитуда колебаний (амплит. волны). w=2p\T.

3.5 энергетические характеристики волн: объёмная плотность энергии волны, поток энергии волны, плотность потока энергии волны, интенсивность волны, спектральная плотность потока энергии излучения. Уровень интенсивности, уровень звукового давления, уровень громкости звука.

При волновом движении происходит перенос энергии, которая состоит из кинетической и потенциальной энергий колеблющихся частиц среды. Причем потенциальная энергия обусловлена деформацией вещества при взаимном смещении частиц. В отличие от колебаний свободного тела в волне не происходит взаимного перехода кинетической и потенциальной энергии частиц. Мгновенные значения той и другой энергии изменяются одновременно (в фазе) соответственно изменению смещения частиц.

Для мгновенного значения энергии (потенциальной и кинетической) одной частицы можно записать:

,(18)

где S- смещение частицы, w- частота колебания частицы, A- амплитуда колебания частицы, V- скорость волнового процесса, в котором участвует частица, m – масса одной частицы.

Из формулы 18 следует, что мгновенные значения энергии каждой частицы среды изменяются во времени с удвоенной частотой колебания, причем в каждый момент времени эти значения для различных частиц отличаются. Однако среднее значение энергии за период колебания для всех частиц одинаково и составляет:

eср =

.

Рассчитаем энергию волны для некоторого объема DV среды, в которой она распространяется.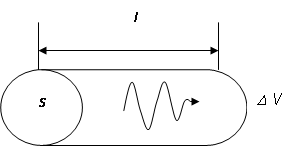

http://www.bestreferat.ru/images/paper/87/48/4454887.png

Если в единице объема среды содержится N частиц, то r = Nm —плотность среды и среднее значение энергии волны в объеме DV будет:

Е_ср =

(19)

где

— объемная плотность энергии волны.

Величина, численно равная средней энергии Е_ср, переносимой волной в единицу времени t через заданную поверхность S, перпендикулярную направлению распространения волны, называется потоком энергии через эту поверхность:

Ф =

(20)

и измеряется в единицах мощности - Вт.

Поток энергии, приходящийся на единицу поверхности, называется плотностью потока энергии:

(21)

и измеряется в Вт/м2. Плотность потока энергии называют также интенсивностью волны.

В векторной форме:

. (22)

Плотность потока энергии, переносимого волной, можно рассматривать как вектор, совпадающий по направлению с вектором скорости волны.

Уровень интенсивности звука = 10 lg (J/J₀) дБ
Поскольку звуки столь сильно различаются по интенсивности, удобнее рассматривать ее как логарифмическую величину и измерять в децибелах. Логарифмическая величина интенсивности представляет собой логарифм отношения рассматриваемого значения величины к ее значению, принимаемому за исходное. Уровень интенсивности J по отношению к некоторой условно выбранной интенсивности J₀ равен

Таким образом, один звук, превышающий другой по уровню интенсивности на 20 дБ, превышает его в 100 раз по интенсивности.

В практике акустических измерений принято выражать интенсивность звука через соответствующую амплитуду избыточного давления Р_е. Когда давление измеряется в децибелах относительно некоторого условно выбранного давления Р₀, получают так называемый уровень звукового давления. Поскольку интенсивность звука пропорциональна величине P_e², а lg(P_e²) = 2lgP_e, уровень звукового давления определяется следующим образом:

Уровень звукового давления = 20 lg (P_e/P₀) дБ

Условное давление Р₀= 2Ч10^—5 Па соответствует стандартному порогу слышимости для звука с частотой 1 кГц.
Уровень громкости звука — относительная величина, которая выражается в фонах и численно равна уровню звукового давления (в децибелах — дБ), создаваемого синусоидальным тоном частотой 1 кГц такой же громкости, как и измеряемый звук (равногромким данному звуку).

3.6 Электромагнитная волна, условие и механизм ее возникновения. Скорость и длина электромагнитной волны в вакууме и в различных средах. Показатель преломления среды. Шкала электромагнитных волн. Характеристика электромагнитных волн различных интервалов длин волн.

Электромагнитные волны-это процесс распространения переменных магнитного и электрического полей. Переменное электрическое поле порождает магнитное, которое оказывается переменным. Оно порождает электрическое. Если возбудить с помощью колеблющихся зарядов переменное электромагнитное поле, то в окружающем заряды пространстве возникнет последовательность взаимных превращений электрического и магнитного полей, распространяющихся от точки к точке.

Скорость в вакууме: Е=М=1 V=C=3*10^8(м/с ) V=C/((E*M)^1/2),

Где E-диэлектрическая проницаемость среды, M-магнитная проницаемость среды.

Показатель преломления(абс.)- отношение скорости волны в вакууме к скорости в среде.

n=C/V =лямда(0)/лямда лямда(0)=С/ню лямда=V/ню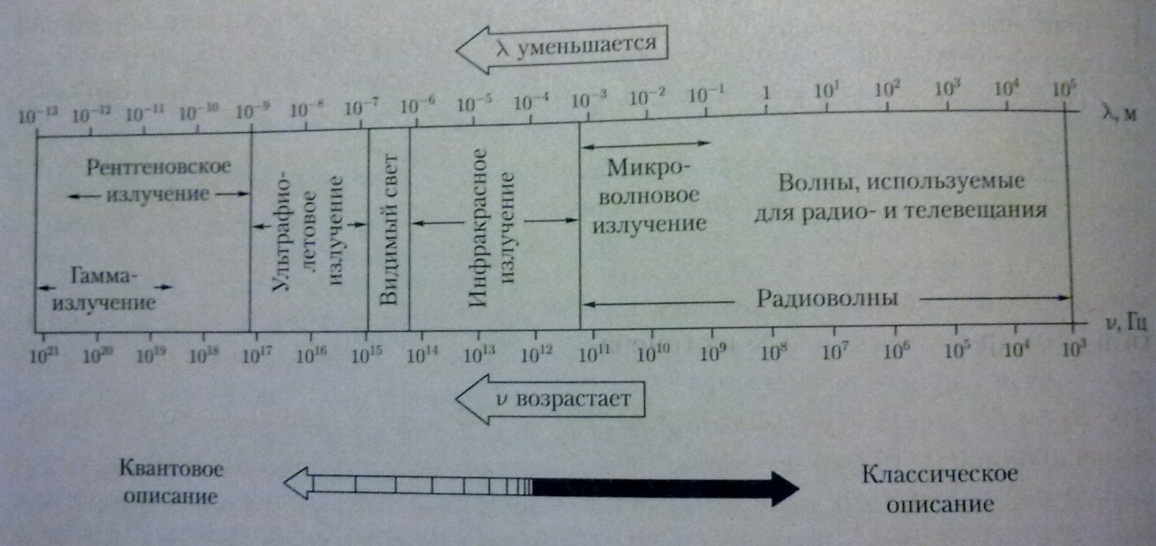

фото0136

3.7 Интерференция когерентных волн. Амплитуда результирующего колебания при интерференции 2х волн, условия максимумов и минимумов амплитуды. Интерференционный спектр.

Интерференция- такое положение когерентных волн, при которой имеет место перераспределение энергии волн в пространстве и устойчивое во времени и пространстве усиление колебаний в одних местах и ослабление в других.

Когерентные волны- волны одинаковой частоты, разность фаз которых не зависит от времени.

1 2 3 4 5