Ответы к экзамену по физике 1 курс. 2 закон Ньютона F ma (докво)

Название	2 закон Ньютона F ma (докво)
Анкор	Ответы к экзамену по физике 1 курс.docx
Дата	18.01.2018
Размер	35.3 Mb.
Формат файла
Имя файла	Ответы к экзамену по физике 1 курс.docx
Тип	Закон #14457
страница	2 из 5

1 2 3 4 5

2.4 Магнитное взаимодействие – это взаимодействие движущихся зарядов.

Магнитное поле создается: движущимися электрическими зарядами, проводниками с током, постоянными магнитами.

1)Индукция магнитного поля(В) – векторная величина, которая является характеристикой магнитного поля. Определяет с какой силой магнитное поле действует на заряд, движущийся со скоростью. (В)=(Тл)

B=Fлmax/qV – если заряд попадает в поле перпендикулярно линиям м. индукции

2)В – это физ величин, равная max силе Ампера, действующей на единичный элемент проводника с током. B=dFamax/Idl

Для определения направления вектора В используют правило правой руки (винта, буравчика).

Для магнитного поля справедлив принцип суперпозиции.

Вектор В является касательным к силовым линиям м. поля.

Если В в каждой точке поля остается постоянным как по величине, так и по направлению, то такое м. поле называется однородным. Такое поле можно создать с помощью бесконечно длиной катушки с током (соленоид).

Напряженность магнитного полянеобходима для определения магнитной индукции поля, создаваемого токами различной конфигурации в различных средах. Напряженность магнитного поля характеризует магнитное поле в вакууме.

Напряженность магнитного поля (формула) векторная физическая величина, равная: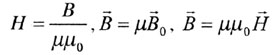

μ0 – магнитная постоян, μ – м. проницаемость среды

Напряженность магнитного поля в СИ - ампер на метр (А/м).

Векторы индукции (В) и напряженности магнитного поля (Н) совпадают по направлению.

Напряженность магнитного поля зависит только от силы тока, протекающего по проводнику, и его геометрии.

Закон Ампера — закон взаимодействия электрических токов. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются.

На проводник с электрическим током, помещенный в магнитное поле действует сила Ампера.

$df = i b dl \sin\alpha\,$ , где $\alpha$ — угол между векторами магнитной индукции и тока.

Сила  максимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции ( $\alpha = 90^\circ, \sin\alpha = 1$ ):

$df_{max} = ibdl\,$ .

Направление определяется по правилу левой руки.

Закон Био — Савара — Лапласа и его применение к расчету магнитного поля

Магнитное поле постоянных токов различной формы изучалось французскими учеными Ж. Био (1774—1862) и Ф. Саваром (1791—1841). Результаты этих опытов были обобщены выдающимся французским математиком и физиком П. Лапласом.

Закон Био — Савара — Лапласа для проводника с током I, элемент dl которого создает в некоторой точке А (рис. 164) индукцию поля dB, записывается в виде

(110.1)

где dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r—радиус-вектор, проведанный из элемента dl проводника в точку А поля, r — модуль радиуса-вектора r. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление dB, если поступательное движение винта соответствует направлению тока в элементе.

Модуль вектора dB определяется выражением

(110.2)

где a — угол между векторами dl и r.

Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности: Напряженность и потенциал поля диполя. Решение задач по физике

(110.3)

Расчет характеристик магнитного поля (В и Н) по приведенным формулам в общем случае сложен. Однако если распределение тока имеет определенную симметрию, то применение закона Био — Савара — Лапласа совместно с принципом суперпозиции позволяет просто рассчитать конкретные поля. Рассмотрим два примера.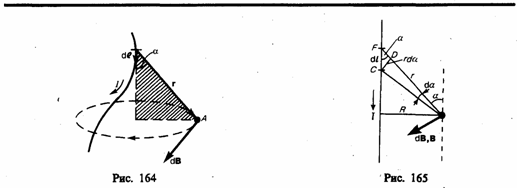

1. Магнитное поле прямого тока — тока, текущего по тонкому прямому проводу бесконечной длины (рис. 165). В произвольной точке А, удаленной от оси проводника на расстояние R, векторы dB от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к вам»). Поэтому сложение векторов dB можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол a (угол между векторами dl и r), выразив через него все остальные величины. Из рис. 165 следует, что

(радиус дуги CD вследствие малости dl равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (110.2), получим, что магнитная индукция, создаваемая одним элементом проводника, равна

(110.4)

Так как угол a для всех элементов прямого тока изменяется в пределах от 0 до p, то, согласно (110.3) и (110.4),

Следовательно, магнитная индукция поля прямого тока

(110.5)

2. Магнитное поле в центре кругового проводника с током (рис. 166). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления — вдоль нормали от витка. Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sina =1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2),

Тогда

Следовательно, магнитная индукция поля в центре кругового проводника с током

Магнитное поле действует только на движущиеся электрические заряды и на частицы и тела, обладающие магнитным моментом.

На электрически заряженную частицу, движущуюся в магнитном поле со скоростью v, действует сила Лоренца, которая направлена всегда перпендикулярно направлению движения. Величина этой силы зависит от направления движения частицы по отношению к вектору магнитной индукции и определяется выражением

→

Движение заряженных частиц в электрическом и магнитном полях.

На заряженную частицу со стороны электрического поля действует постоянная сила F=qE , которая сообщает частице постоянное ускорение $latex: </h2>\vec a = \frac{\vec f}{m} = \frac{q \vec e}{m}$ .

При движении заряженной частицы в однородном постоянном магнитном поле на нее действует сила Лоренца $latex: </h2>\vec f_l$ . Если начальная скорость $latex: </h2>\vec \upsilon_0$ частицы перпендикулярна вектору магнитной индукции $latex: </h2>\vec b$ поля, то заряженная частица движется по окружности.

2.5 Работа магнитного поля при движении проводника с током.

На проводник с током в магнитном поле действуют силы, которые определяются с помощью закона Ампера. Если проводник не закреплен, то под действием силы Ампера он в магнитном поле будет перемещаться. Значит, магнитное поле совершает работу по перемещению проводника с током.

Для вычисления этой работы рассмотрим проводник длиной l с током I (он может свободно двигаться), который помещен в однородное внешнее магнитное поле, которое перпендикулярно плоскости контура. Сила, направление которой определяется по правилу левой руки, а значение — по закону Ампера, рассчитывается по формуле

Под действием данной силы проводник передвинется параллельно самому себе на отрезок dx из положения 1 в положение 2. Работа, которая совершается магнитным полем, равна

так как ldx=dS — площадь, которую пересекает проводник при его перемещении в магнитном поле, BdS=dФ — поток вектора магнитной индукции, который пронизывает эту площадь. Значит,

т. е. работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником.

Магнитный поток (Ф)=(Вебер,Вб).

1)Магнитным потоком называется физ величина, численно равная скалярному произведению потока вектора магнитной индукции на площадь малой площадки.

dФ = BdS(вектор), где dS(вектор) = n(вектор)dS. n(вектор) – нормаль к площадке, dS – размер площадки

dФ = BdS = BdScosa = BndS, угол а = (n,B), Bn = Bcosa

2) Магнитным потоком через произвольную пов-ть S называется скалярная физ величина, численно равная интегралу, взятому по пов-ти S от скалярного произведения BdS

3) Потоком вектора Ф через замкнутую пов-ть называется интеграл, взятый от B*dS

Теорема Гаусса. В соответствии с теоремой Гаусса для магнитной индукции поток вектора магнитной индукции через любую замкнутую поверхность равен нулю: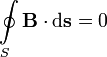

$\oint\limits_s \mathbf{b} \cdot \text{d} \mathbf{s} = 0$

Физический смысл: эта теорема утверждает, что магнитных зарядов в природе не существует.

Индуктивность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность, краем которой является этот контур.

$\displaystyle \phi = li$

$\displaystyle \phi$ — магнитный поток,  — ток в контуре,  — индуктивность

Индуктивность соленоида:

Магнитная индукция в соленоиде определяется по формуле:

где μ₀ - магнитная постоянная, равна 4p×10^-7 Гн/м,

μ - магнитная проницаемость среды, заполняющей соленоид,

N - число витков соленоида,

I - сила тока.

Магнитный поток через N витков соленоида будет равен

,

где S – площадь сечения соленоида. Сравнивая формулы легко найти, что индуктивность соленоида

2.6 Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.

1)Электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром.

Величина электродвижущей силы (ЭДС) не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.

Согласно закону электромагнитной индукции Фарадея:

$\mathcal{e} = - {{d\phi_b} \over dt}$ , $\phi_b\!$ — магнитный поток через один виток.

2) Рассмотрим возникновение ЭДС индукции в прямоугольном контуре, помещенном в однородное магнитное поле В перпендикулярное плоскости контура.

Пусть одна из сторон контура длиной l скользит со скоростью  по двум другим сторонам

На свободные заряды на этом участке контура действует сила Лоренца. Одна из составляющих этой силы, связанная с переносной скоростью  зарядов, направлена вдоль проводника. Эта составляющая указана на рис. 1.20.3. Она играет роль сторонней силы. Ее модуль равен

F_Л = eυB

Работа силы F_Л на пути l равна

A = F_Л · l = eυBl.

По определению ЭДС

В других неподвижных частях контура сторонняя сила равна нулю. Соотношению для _инд можно придать привычный вид. За время Δt площадь контура изменяется на ΔS = lυΔt. Изменение магнитного потока за это время равно ΔΦ = BlυΔt. Следовательно,

Самоиндукция — возникновение ЭДС индукции в замкнутом проводящем контуре при изменении тока, протекающего по контуру.

При изменении тока в контуре пропорционально меняется и магнитный поток через поверхность, ограниченную этим контуром. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС. Это явление и называется самоиндукцией.

Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока — убыванию (сонаправлена с током).

$\mathcal e = -l \frac{di}{dt}$ .

Коэффициент пропорциональности  называется коэффициентомсамоиндукции или индуктивностью контура (катушки).

Энергия магнитного поля.

Проводник, c протекающим по нему электрическим ток, всегда окружен магнитным полем, причем магнитное поле исчезает и появляется вместе с исчезновением и появлением тока. Магнитное поле, подобно электрическому, является носителем энергии. Логично предположить, что энергия магнитного поля совпадает с работой, затрачиваемой током на создание этого поля.

Рассмотрим контур индуктивностью L, по которому протекает ток I. С этим контуром сцеплен магнитный поток Ф=LI, поскольку индуктивность контура неизменна, то при изменении тока на dI магнитный поток изменяется на dФ=LdI. Но для изменения магнитного потока на величину dФ следует совершить работу dА=IdФ=LIdI.

Тогда работа по созданию магнитного потока Ф равна

Значит, энергия магнитного поля, которое связано с контуром,

1 2 3 4 5