Занятие 13. Контрольные вопросы для подготовки к занятию Сформулируйте, запишите математическое выражение закона Био Савара Лапласа и поясните его
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
Занятие 13 ЗАКОН БИО – САВАРА – ЛАПЛАСА Учебная цель: добиться понимания физической сущности закона Био - Савара - Лапласа, принципа суперпозиции для магнитного поля элементов тока и научиться применять их для расчета магнитных полей проводников с током. Литература Основная: Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высшая школа, 1989. – Гл. 22, § 22.1, 22.2, 22.3. Дополнительная: Савельев И.В. Курс общей физики. – М.: Наука, 1989. – Т. 2, гл. 6, § 39 - 42. Контрольные вопросы для подготовки к занятию 1. Сформулируйте, запишите математическое выражение закона Био - Савара - Лапласа и поясните его. 2. По какому правилу определяется направление вектора магнитной индукции (напряженности) элемента тока? 3. Запишите выражение закона Био - Савара - Лапласа для напряженности магнитного поля элемента тока. 4. Сформулируйте и поясните принцип суперпозиции магнитных полей. 5. Как рассчитывается величина индукции (напряженности) магнитного поля в случае, если направление индукции (напряженности) элементов тока данного проводника одинаковы? 6. Сформулируйте, запишите выражение и поясните закон полного тока (теорему о циркуляции напряженности магнитного поля). 7. Сформулируйте и объясните правило выбора знаков токов, охватываемых данным контуром. 8. По какой формуле рассчитывается индукция (напряженность) магнитного поля: - прямого проводника конечной длины с током на расстоянии r от его оси; - бесконечно длинного проводника; - в центре прямоугольного проводника с током; - на оси кругового витка радиусом R с током I? 9. Запишите выражение индукции (напряженности) магнитного поля соленоида и поясните его. 10. Что называется длинным соленоидом (нормальной катушкой), каким является его поле? 11. Запишите выражение для индукции (напряженность) магнитного поля в произвольной точке соленоида конечной длины с током I. Краткие теоретические сведения и основные формулы Закон Био – Савара – Лапласа позволяет определить величину и направление магнитной индукции в любой точке магнитного поля, создаваемого бесконечно малым элементом проводника с током I – элементом тока (Idl). Согласно этому закону, элемент проводника dl с током I (рис. 13.1) создает в некоторой точке С магнитное поле, индукция которого dB пропорциональна длине dl, силе тока I, синусу угла между направлением тока и радиус-вектором  точки С и обратно пропорциональна квадрату расстояния точки С и обратно пропорциональна квадрату расстояния 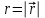 , т.е. , т.е. 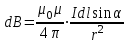 , ,где 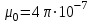 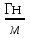 - магнитная постоянная; - безразмерная величина, характеризующая магнитные свойства среды и называемая магнитной проницаемостью среды. - магнитная постоянная; - безразмерная величина, характеризующая магнитные свойства среды и называемая магнитной проницаемостью среды. 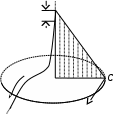 Рис. 13.1 В векторной форме закон Био - Савара - Лапласа имеет вид  . (13.1) . (13.1)Направление 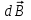 определяется по правилу векторного произведения, или по правилу обхвата правой руки. Вектор определяется по правилу векторного произведения, или по правилу обхвата правой руки. Вектор 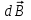 направлен перпендикулярно к плоскости, в которой лежат векторы направлен перпендикулярно к плоскости, в которой лежат векторы 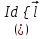 и и  , таким образом, что из конца вектора , таким образом, что из конца вектора 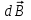 поворот поворот 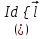 до совмещения с до совмещения с  по кратчайшему пути виден происходящим против часовой стрелки. по кратчайшему пути виден происходящим против часовой стрелки.Наглядно правило векторного произведения на практике заменяется правилом обхвата правой руки: отставленный под прямым углом большой палец правой руки направляют по направлению тока в проводнике, концы загнутых четырех пальцев, охватывающих проводник с током, помещенных в заданную точку магнитного поля, покажут направление вектора 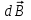  в этой точке. в этой точке.Учитывая, что векторы магнитной индукции и напряженности связаны соотношением 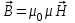 или или 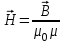 , (13.2) , (13.2)для напряженности 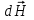 закон Био - Савара - Лапласа примет вид закон Био - Савара - Лапласа примет вид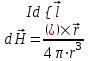 . (13.3) . (13.3) Величина вектора 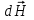 равна равна . (13.4) . (13.4)Для магнитных полей, так же как и для электростатических, соблюдается принцип суперпозиции: при наложении нескольких магнитных полей, имеющих магнитные индукции  , ,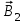 , , ,..., ,..., , магнитная индукция результирующего поля , магнитная индукция результирующего поля  равна геометрической сумме магнитных индукций складываемых полей: равна геометрической сумме магнитных индукций складываемых полей: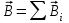  . .Закон Био - Савара - Лапласа (13.1) и (13.3) представлен в виде дифференциального уравнения для магнитной индукции и напряженности, создаваемых небольшим участком проводника 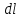 . Для вычисления полной магнитной индукции . Для вычисления полной магнитной индукции  или напряженности или напряженности 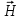 магнитного поля, создаваемого в точке с током магнитного поля, создаваемого в точке с током  , идущим по проводнику конечной длины , идущим по проводнику конечной длины 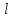 надо геометрически суммировать элементарные индукции надо геометрически суммировать элементарные индукции 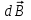 (напряженности (напряженности 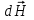 ), создаваемые всеми элементами тока ), создаваемые всеми элементами тока 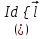 : :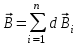 , , 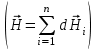 . .Если индукция магнитного поля 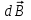 от всех элементов тока от всех элементов тока 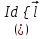 направлены вдоль одной прямой, то геометрическое суммирование сводится к алгебраическому суммированию, т.е. к интегрированию: направлены вдоль одной прямой, то геометрическое суммирование сводится к алгебраическому суммированию, т.е. к интегрированию: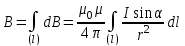 ; (13.5) ; (13.5) . (13.6) . (13.6)Знак (l) показывает, что интегрирование производится по всей длине l проводника. Магнитные индукции и напряженности простейших магнитных полей 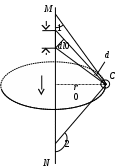 1. Магнитная индукция и напряженность магнитного поля прямого проводника с током I на расстоянии r0 от него (рис. 13.2): 1. Магнитная индукция и напряженность магнитного поля прямого проводника с током I на расстоянии r0 от него (рис. 13.2): Рис. 13.2  ; (13.7) ; (13.7)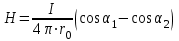 . (13.8) . (13.8)где 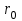 - кратчайшее расстояние от точки С до проводника; 1 и 2 – углы, которые образуют радиус-векторы, проведенные в точку С из начала и конца проводника. - кратчайшее расстояние от точки С до проводника; 1 и 2 – углы, которые образуют радиус-векторы, проведенные в точку С из начала и конца проводника.Для бесконечно длинного ( 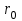 << l) прямого проводника 10, 2, поэтому << l) прямого проводника 10, 2, поэтому ; (13.9) ; (13.9) . (13.10) . (13.10)2. Магнитная индукция и напряженность в центре прямоугольного проводника с током:  ; (13.11) ; (13.11)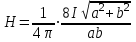 , (13.12) , (13.12)где aиb – стороны прямоугольника. 3. Магнитная индукция и напряженность магнитного поля на оси кругового витка радиуса R с током I (рис. 13.3):  Рис. 13.3 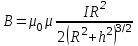 ; (13.13) ; (13.13)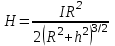 , (13.14) , (13.14)где h – расстояние до центра витка; R – радиус витка. Магнитная индукция и напряженность магнитного поля в центре витка (h = 0): 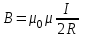 ; (13.15) ; (13.15)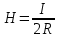 . (13.16) . (13.16)Закон Био – Савара – Лапласа и принцип суперпозиции лежат в основе первого метода расчета магнитных полей. В основе второго метода лежит теорема о циркуляции напряженности магнитного поля (закон полного тока): циркуляция вектора напряженности магнитного поля по произвольному замкнутому контуру равна алгебраической сумме токов, охватываемых этим контуром: 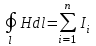 . (13.17) . (13.17)Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого связано с направлением обхода контура правилом правого винта, ток противоположного направления считается отрицательным. Магнитная индукция и напряженность поля короткого соленоида в произвольной точке С, лежащей на оси (рис. 13.4):                                               . . . . . . . . . . . . . . R  ++++++++++++++ L 1  2 |
