|
|
Занятие 13. Контрольные вопросы для подготовки к занятию Сформулируйте, запишите математическое выражение закона Био Савара Лапласа и поясните его

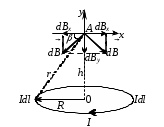
Рис. 13.9
Решение
а) На оси кольца.
Найдем направление индукции 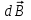 , созданной элементами тока , созданной элементами тока 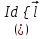 , лежащими на одном диаметре кольца. Они направлены под углом к оси х (рис. 13.9). , лежащими на одном диаметре кольца. Они направлены под углом к оси х (рис. 13.9).
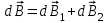 (для двух диаметрально противоположных элементов). (для двух диаметрально противоположных элементов).
Спроецируем 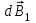 и и 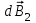 на оси х и у: на оси х и у:
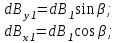
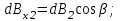 
 ; ; 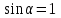 , ,
так как 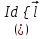 перпендикулярно r. перпендикулярно r.
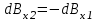 ; ;
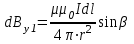 ; ;
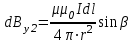 . .
Сумма проекций векторов dB на ось х будет равна нулю, то есть Вх тоже равна нулю.
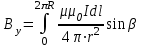 ; ; 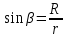 ; ;  . .
Интегрируя, получаем
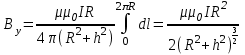 ; ;  ; ;
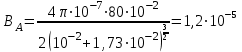 Тл. Тл.
б) в центре кольца h = 0, r = R (рис. 13.10):
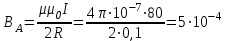 
Тл.
Рис. 13.10
Ответ: а) 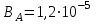 Тл; б) Тл; б) 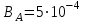 Тл. Тл.
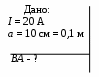
З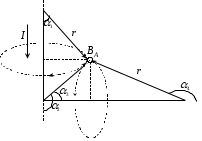
адача 4. По длинному прямому проводу, согнутому под прямым углом, течет ток I = 20 А. Найти магнитную индукцию  в точке, лежащей на биссектрисе угла и отстоящей от вершины угла на а = 10 см (рис. 13.11). в точке, лежащей на биссектрисе угла и отстоящей от вершины угла на а = 10 см (рис. 13.11).
Рис. 13.11
Решение
1. Нарисуем линии индукции магнитного поля для каждого отрезка провода. Линии должны проходить через заданную точку, лежать в плоскости, перпендикулярной току, и иметь центр на проводнике с током (рис. 13.11). Направление линии индукции определим по правилу буравчика. Касательные к силовым линиям перпендикулярны плоскости чертежа и векторы 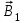 и и 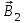 направлены «к нам». направлены «к нам».
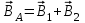 . Так как . Так как  и и 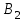 направлены в одну сторону по одной прямой, то направлены в одну сторону по одной прямой, то 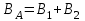 . .
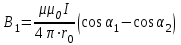 - индукция от вертикальной части провода; 1 0, 2 = 135. - индукция от вертикальной части провода; 1 0, 2 = 135.
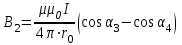 - индукция от горизонтальной части провода; - индукция от горизонтальной части провода; 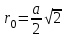 ; 3 = 45. ; 3 = 45.
4 , так как провод ограничен вершиной угла слева и бесконечен справа (рис. 13.11).
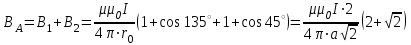 . .
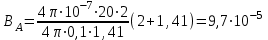 Тл. Тл.
Ответ: 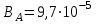 Тл. Тл.
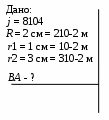

Рис. 13.12
З 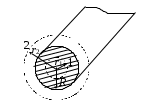
адача 5. По сплошному бесконечному цилиндрическому проводнику радиусом R = 2 см течет ток плотностью j= 8104 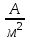 . Рассчитать магнитное поле внутри и вне проводника (рис. 13.12). . Рассчитать магнитное поле внутри и вне проводника (рис. 13.12).
Решение
На рисунке изображено поперечное сечение проводника с двумя точками на расстояниях r1 и r2 от оси проводника. Необходимо вычислить индукцию магнитного поля в этих точках.
Закон Био – Савара – Лапласа применить нельзя, так как проводник не тонкий. Для решения задачи применим закон полного тока:
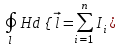 . .
Циркуляция напряженности магнитного поля по произвольному замкнутому контуру равна алгебраической сумме токов, охватываемых контуром.
Для точки 1, находящейся внутри проводника, выберем в качестве контура обхода окружность, центр которой лежит на оси проводника, а радиус равен r1 – расстоянию от центра до данной точки.
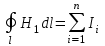 ; ; 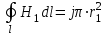 ; ; 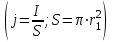 ; ;
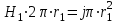 ; ; 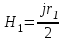 ; ; 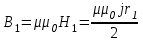 . .
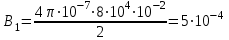 Тл. Тл.
Точка 2 находится вне проводника. Контур обхода – окружность радиусом r2, проходящая через точку 2. Охватываемые токи проходят через площадь 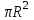 - в проводнике, радиус которого равен R. - в проводнике, радиус которого равен R.
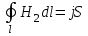 ; ; 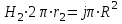 ; ;
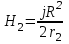 ; ; 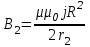 ; ; 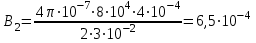 Тл. Тл.
Полученные соотношения дают возможность построить график зависимости индукции магнитного поля сплошного цилиндрического проводника от расстояния r в любой точке внутри и вне проводника (рис. 13.13).
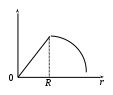
Рис. 13.13
Ответ: 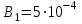 Тл; Тл; 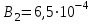 Тл. Тл.
Задачи для самостоятельного решения
Задача 1. По бесконечному прямому проводнику идёт ток 20 А. Проводник образует петлю, радиус которой R = 2 см. Определить индукцию магнитного поля в центре петли по величине и направлению (рис. 13.14).
Ответ: В = 4,2710-4 Тл.

Рис. 13.4 Рис. 13.5
Задача 2. Два очень длинных прямых параллельных друг другу провода соединены на одном конце полукольцом радиусом R = 2,5 см. Чему равна индукция магнитного поля, созданного проводами в центре полукольца, если ток в проводах I = 12 А (рис. 13.15).
Ответ: 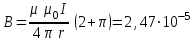 Тл. Тл.
Задача 3. Прямой бесконечно длинный провод с током I = 10 А образует в середине кольцевой виток радиусом R = 3 см, плоскость которого перпендикулярна проводу. Определить индукцию магнитного поля по величине и направлению в точке, лежащей в центре витка (рис. 13.16).

Ответ: В = 2,210-4 Тл.
Задача 4. Два бесконечных прямых провода с токами I1 = 8 А и I2 = = 12 А расположены во взаимно перпендикулярных плоскостях. Найти индукцию магнитного поля в точке, лежащей на расстоянии 3 см от первого провода и 2 см от второго провода (рис. 13.17).
Ответ: В = 13,110-5 Тл.
Задача 5. По прямому бесконечно длинному проводу течёт ток I1 = = 3,14 А. Круговой виток с током I2 = 3 А радиусом R = 30 см расположен так, что плоскость его параллельна прямому проводнику, а перпендикуляр, опущенный из центра витка на провод, является нормалью к плоскости витка. Расстояние от центра витка до провода равна d = 20 см. Найти индукцию магнитного поля в центре витка (рис. 13.18).
Ответ: B = 710-6 Тл.
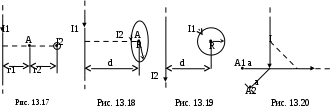
Задача 6. Круговой виток радиусом R = 3 см с током I1 = 3 А лежит в одной плоскости с бесконечно длинным прямым током I2 = 6 А. Расстояние от центра до провода равно d = 10 см. Определить индукцию магнитного поля в центре витка (рис. 13.19).
Ответ: В = 5,0810-5 Тл.
Задача 7. Бесконечный прямой провод с током I = 20 А согнут под прямым углом. Определить индукцию магнитного поля в точке А1, лежащей на продолжении горизонтальной части провода, на расстоянии а = 20 см от вершины угла (рис. 13.20).
Ответ: ВА = 10-5 Тл.
Задача 8. Бесконечный прямой провод с током I = 100 А согнут под прямым углом. Определить индукцию магнитного поля в точке А2 (рис. 13.20), лежащей на биссектрисе угла на расстоянии а = 10 см от вершины угла.
Ответ: ВА = 8,2810-5 Тл.
Задача 9. Провод согнут в виде прямоугольника со сторонами а = = 3 см и b = 4 см. По проводу идёт ток I = 50 А. Определить величину и направление индукции магнитного поля в центре прямоугольника.
Ответ: В = 1,6710-3 Тл.
Задача 10. Провод длиной 1 м согнут в виде квадрата. По проводу течёт ток I = 10 А. Определить индукцию магнитного поля в центре квадрата.
Ответ: В = 4,510-5 Тл.
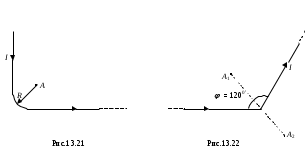
Задача 11. По бесконечно длинному проводнику, согнутому, как показано на рис. 13.21, течёт ток I = 100 А. Определить магнитную индукцию В в точке А, если радиус закругления R = 10 см. Закругление представляет собой четверть окружности.
Ответ: ВА = 3,5710-4 Тл.
Задача 12. Прямой бесконечно длинный проводник с током I = 50 А согнут так, что между частями его образовался угол = 1200. Определить индукцию магнитного поля в точках, лежащих на биссектрисе угла и удалённых от вершины его на расстояние а = 5 см (рис. 13.22).
Ответ: 1) В1 = 3,4610 - 4 Тл; 2) В2 = 1,1610-4 Тл.
Задача 13. По тонкому проволочному кольцу течёт ток. Не изменяя силы тока в проводнике, ему придали форму квадрата. Во сколько раз изменилась магнитная индукция в центре кольца?
Ответ: 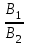 = 1,14 раза. = 1,14 раза.
Задача 14. По контуру в виде равностороннего треугольника течёт ток I = 40 А. Сторона треугольника а = 30 см. Определить магнитную индукцию 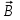 в точке пересечения высот. в точке пересечения высот.
Ответ: В = 2,410-4 Тл.
Задача 15. По проводнику в виде тонкого кольца радиусом R = 10 см течёт ток I = 80 А. Найти магнитную индукцию В в точке, равноудалённой от всех точек кольца на r = 20 см.
Ответ: В = 6,2810-5 Тл.
Задача 16. По проводнику в виде тонкого кольца радиусом R = 10 см течёт ток. Чему равна сила этого тока, если индукция магнитного поля в точке А (рис. 13.23) В = 10-5 Тл. Угол = 100.
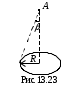
Ответ: I = 61,2 А.
Задача 17*. Напряжённость магнитного поля 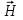 в центре кругового витка радиусом r= 8 см равна 30 в центре кругового витка радиусом r= 8 см равна 30 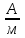 . Определить напряжённость поля на оси витка в точке, расположенной на расстоянии d = 6 см от центра витка. . Определить напряжённость поля на оси витка в точке, расположенной на расстоянии d = 6 см от центра витка.
Ответ: Н = 15,4 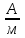 . .
Задача 18*. По контуру, согнутому в виде правильного шестиугольника, длина стороны которого а = 20 см, течёт ток I = 100 А. Найти напряжённость магнитного поля в центре шестиугольника. Для сравнения определить напряжённость Н0 в центре кругового провода, совпадающего с окружностью, описанной около данного шестиугольника.
Ответ: Н = 275 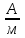 ; Н0 = 250 ; Н0 = 250 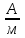 . .
Задача 19. По контуру в виде квадрата идёт ток I = 50 А. Сторона квадрата а = 20 см. Чему равна магнитная индукция в точке пересечения диагоналей?
Ответ: В = 2,8210-4 Тл.
Задача 20. Два длинных параллельных провода находятся на расстоянии d = 5 см один от другого. По проводам текут одинаковые токи в противоположных направлениях силой I = 10 А каждый. Найти напряжённость магнитного поля в точке, находящейся на расстоянии  = 2 см от одного провода и = 2 см от одного провода и 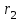 = 3 см от другого. = 3 см от другого.
Ответ: Н = 132 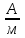 . .
Задача 21. Расстояние между двумя параллельными токами d = 5 см. По проводам в одном направлении текут токи I = 30 А каждый. Найти напряжённость магнитного поля в точке, находящейся на расстоянии  = 4 см от одного и = 4 см от одного и 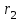 = 3 см от другого провода. = 3 см от другого провода.
Ответ: Н = 200 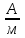 . .
Задача 22. По двум бесконечно длинным параллельным проводникам текут токи I1 = 50 А и I2 = 100 А в противоположных направлениях. Расстояние между проводниками d = 20 см. Определить магнитную индукцию В в точке, удалённой от первого проводника на  = 25 см и от второго на = 25 см и от второго на 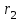 = 40 см. = 40 см.
Ответ: В = 8,810-5 Тл.
Задача 23. По двум параллельным прямым бесконечно длинным проводникам текут токи I1 = 20 А и I2 = 30 А в одном направлении. Расстояние между проводниками d = 10 см. Вычислить индукцию магнитного поля В в точке, удалённой от обоих проводников на одинаковое расстояние r = 10 см.
Ответ: В = 8,7210-5 Тл.
Задача 24. Два бесконечно длинных прямых проводника скрещены под прямым углом. По проводникам текут токи I1 = 80 А и I2 = 60 А. Расстояние между проводниками d = 10 см. Чему равна индукция магнитного поля в точке А, одинаково удалённой от обоих проводников (рис. 13.24).
Ответ: В = 410-4 Тл.
Задача 25. По двум бесконечно длинным прямым проводникам, скрещенным под прямым углом, текут токи I1 = 30 А и I2 = 40 А. Расстояние между проводниками d = 20 см. Определить магнитную индукцию 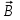 в точке С (рис. 13.24), одинаково удалённой от обоих проводников на расстояние, равное d. в точке С (рис. 13.24), одинаково удалённой от обоих проводников на расстояние, равное d.
Ответ: В = 510-5 Тл. |
|
|
 Скачать 0.74 Mb.
Скачать 0.74 Mb.