Ответы по ЭММ(прошлогодние). 2011г. История возникновения экономикоматематических методов (эмм)

• Название: 2011г. История возникновения экономикоматематических методов (эмм)
• Анкор: Ответы по ЭММ(прошлогодние).doc
• Дата: 04.07.2018
• Размер: 0.5 Mb.
• Имя файла: Ответы по ЭММ(прошлогодние).doc
• Тип: Документы; #21057
• страница: 1 из 3

Мат-мех УрГУ.

Заочное отделение.

Ответы к зачету

Экономико-математическое

моделирование

ПИЭ-4

Екатеринбург

2011г.

1. 
   История возникновения экономико-математических методов (ЭММ).
   

Основоположник французский придворный ученый Людвига XV Кене. В 1758 году он напечатал «Экономическую таблицу» с объяснениями. Задался изучением вопроса: в силу чего пустеет казна? Составил графико-математическую модель воспроизводства, потребления, распределения, накопления. Это первая экономическая модель. Развитие и применение этой модели активно пошло в 40-х годах XIX века. Ученые (Курко, Парас, Праето) представители этой школы ввели ряд новых экономических понятий (их считали аксиомами в экономике). Далее на оснований этих аксиом были построены теории, которые были приближены к реальности. Недостаток теорий в том, что они не могли найти в то время конкретного применения. Они считались абстрактными. Взамен полит-экономического направления было создано статистическое направление. На основе статистических данных в среде производства предлагали прогнозные модели. Считалось, что если накопиться много данных, то теория возникнет сама собой. Проводился анализ многих лет и делался прогноз на следующий год. Преуспела школа «Гарвардский барометр». Исследования показали, что фондовые и товарные рынки взаимосвязаны, то есть можно было сделать прогноз. (Какие изменения одного рынка могут привести к каким изменениям другого). В России тоже развивался этот метод вначале 20-х годов, были созданы балансовые модели. С конца 30-х годов XX века стал применяться экономический подход. На реальных данных выдвигались теории. Эти подходы применялись такими экономистами как Либре, Леонтьев. Затем стали развиваться методы оптимизации и задачи линейного программирования. В 30-м году была сформулирована транспортная задача (Толстой). В 39-м году Конторович сформулировал задачу ЛП. Данциг предложил симплекс-метод решения задач ЛП. Далее в 1945г американцами была изобретена электронная машина – ЭВМ. Появлялись новые дисциплины, связанные с ЭММ. Появились впоследствии Центральный Экономико-математический Институт, Институт Кибернетики в Киеве для разработки методов и их применения. Термин ЭММ предложил Немчинов в 1962 году.

2. 
   Системный анализ, его этапы.
   

Системный анализ это наука о исследовании сложных систем. Система – совокупность взаимосвязанных элементов. Они разделяются на простые и сложные. Сложные характеризуются большой степенью открытости, стохастичности, большой структурированностью.

Развитие методологий:

1. 
   Системный подход – отношение к рассматриваемому объекту, как к системе.
   
2. 
   Развитие классов методологии для классов систем.
   
3. 
   Системные исследования – более углубленно изучает структуру.
   
4. 
   Системный анализ – включает 2) и 3) и выделяет этапы выведения методологий. Большое внимание уделяет цели решения, определяет варианты решений, предполагает выбор оптимального варианта.
   

Этапы системного анализа:

1. 
   Постановка задачи – содержательное описание проблемы: дается характеристика объекта исследования, формулируются все проблемы, мешающие его продвижению вперед и намечаются возможные пути решения проблемы. Обычно задачу ставят люди из системного анализа, а не люди из системы.
   
2. 
   Структуризация системы – определить границы системы, определяются вертикали и горизонтали (связи) системы. Суть вертикальных – связи подчиненности, горизонтальные – связи между смежными системами. Определяют входы-выходы – связи с элементами других систем.
   
3. 
   Построение модели
   
4. 
   Исследование и применение модели
   

3. 
   Моделирование как метод научного познания.
   

Модель – приближенное упрощенное представление о реальном объекте (посредник между объектом системы и субъектом).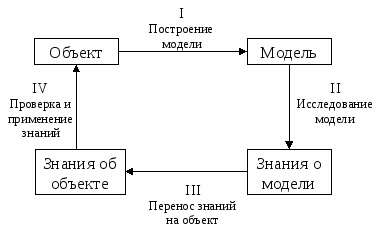



Модель называется адекватной если она обеспечивает точность, достаточную для целей. Адекватность проверяется экспериментом: с помощью пассивного или активного. Пассивный – исследователь только наблюдает модель и ничего не меняет; активный – исследователь вмешивается в структуру модели с тем, чтобы добиться на входе тех сочетаний значения параметра, с которым можно эффективно проверить модель.

4. 
   Виды моделей.
   

Материальные		Знаковые
Масштабные	Аналоговые	Описательные	Графические	Математические
Копия модели в уменьшенном масштабе с сохранением существенных черт. Макеты самолетов, игрушек, зданий…	Аналогия физических процессов, протекающих в разных средах. Системы каналов, трубопроводов	Рассказ об объекте системы, словесный портрет преступника, анкеты.	Планы, схемы, графики, фото.	Математические соотношения, зависимости.

5. 
   Сущность математического моделирования.
   

Математические модели связывают воедино параметры системы. Параметры могут представлять из себя неизвестные величины, которые надо найти. Для этого выделяются существенные параметры.

y (вектор) – неизвестные - внутренние (эндогенные) параметры

x (вектор) – воздействие внешней среды на наш объект, которые мы можем измерять

a (вектор) – технологические параметры системы – например, нормативы, тактико-технические характеристики оборудования.

x, a – экзогенные параметры.

Каждый параметр меняется в своей области изменения. Переменные могут быть непрерывными, целочисленными или случайными величинами.

Когда параметры выделены, возникает необходимость объединить их зависимостью – математической моделью.

Существующие модели:

1. 
   Структурные модели.
   

Неизвестные явно выражается через другие параметры: y = f(x,a).-системы равенств

Или неявно: φ(y, x, a) = 0.

2. 
   Слабоструктурированные модели. Принятие решений в условиях неопределённости. (Вероятностные модели, задачи мат.статистики и теории игр (проблема представляется в виде конфликта)).
   
3. 
   Функциональные модели. В этих моделях сущность проявляется через её проявление, функционирование, реагирование. О структуре D данных нет. Известно, что, если на вход подать X, то получим Y. Система «чёрный ящик». Y = D(x). D (оператор модели) – неизвестна.
   

Другие модели:

4. 
   Оптимизационные модели.
   
5. 
   Теоретико-множественные модели
   
6. 
   Машинные (индукционные) модели.
   
7. 
   Эвристические модели.
   

Модель можно дезагрегировать – разбиение большой модели на несколько более мелких блоков – модель меньших размеров проще проанализировать, набрать опыта. Часто крупные модели являются агрегациями более мелких моделей.

6. 
   Классификация ЭММ.
   

Классы:

1. 
   Экономические приложения математической статистики
   
2. 
   Математическая экономика и эконометрика
   
3. 
   Теория принятия оптимальных решений
   
4. 
   Экономическая кибернетика
   
5. 
   Экспериментальные методы в экономике
   

I. Экономические приложения математической статистики.
Математическая статистика – это научная дисциплина о числе объектов, характеризующихся некоторыми свойствами в рамках общей (генеральной) совокупности. Можно выделить отдельные дисциплины.

1. 
   Выборочный метод – характеризуется тем, что из всей совокупности случайным образом выбирается конечное или ограниченное подмножество, исследуется, определяются законы поведения этой выделенной совокупности, и они распространяются, с некоторыми оговорками (вероятностью) на всю совокупность в целом.
   
2. 
   Корреляционный анализ – высчитывает коэффициенты корреляции – определяется степень зависимости случайных величин, насколько тесно они связаны.
   
3. 
   Регрессионный анализ – определяются сами зависимости между случайными величинами (уравнения регрессии).
   
4. 
   Факторный анализ – определяет те случайные факторы, от которых зависит протекание данного процесса.
   
5. 
   Дисперсионный анализ – устанавливает зависимости между отдельными факторами.
   

II. Математическая экономика и эконометрика
Берутся экономические аксиомы, формализуются и на их основе используются численные методы. Выводится теория, которая должна интерпретироваться на практике (на системе).

1. 
   Теория экономического роста – речь идет о макропараметрах экономических систем (укрупнённых – работают в масштабах страны или отдельного региона) и рассматриваются условия, при которых экономика поступательно развивается. Пример – модель фон Неймана. Макропараметры: национальный доход, капиталовложения, инвестиции.
   
2. 
   Теория производственных функций. y = f(x,a)
   

x – вектор ресурсов

y – вектор выпуска продукции

a – технологический вектор

3. 
   Теория межотраслевого баланса (связи отраслей в народном хозяйстве).
   
4. 
   Теория фирм, теория конкуренции
   
5. 
   Эконометрика – сочетает методы математической статистики с методами экономики.
   

III. Теория принятия оптимальных решений

1. 
   Классическая задача математического программирования:
   

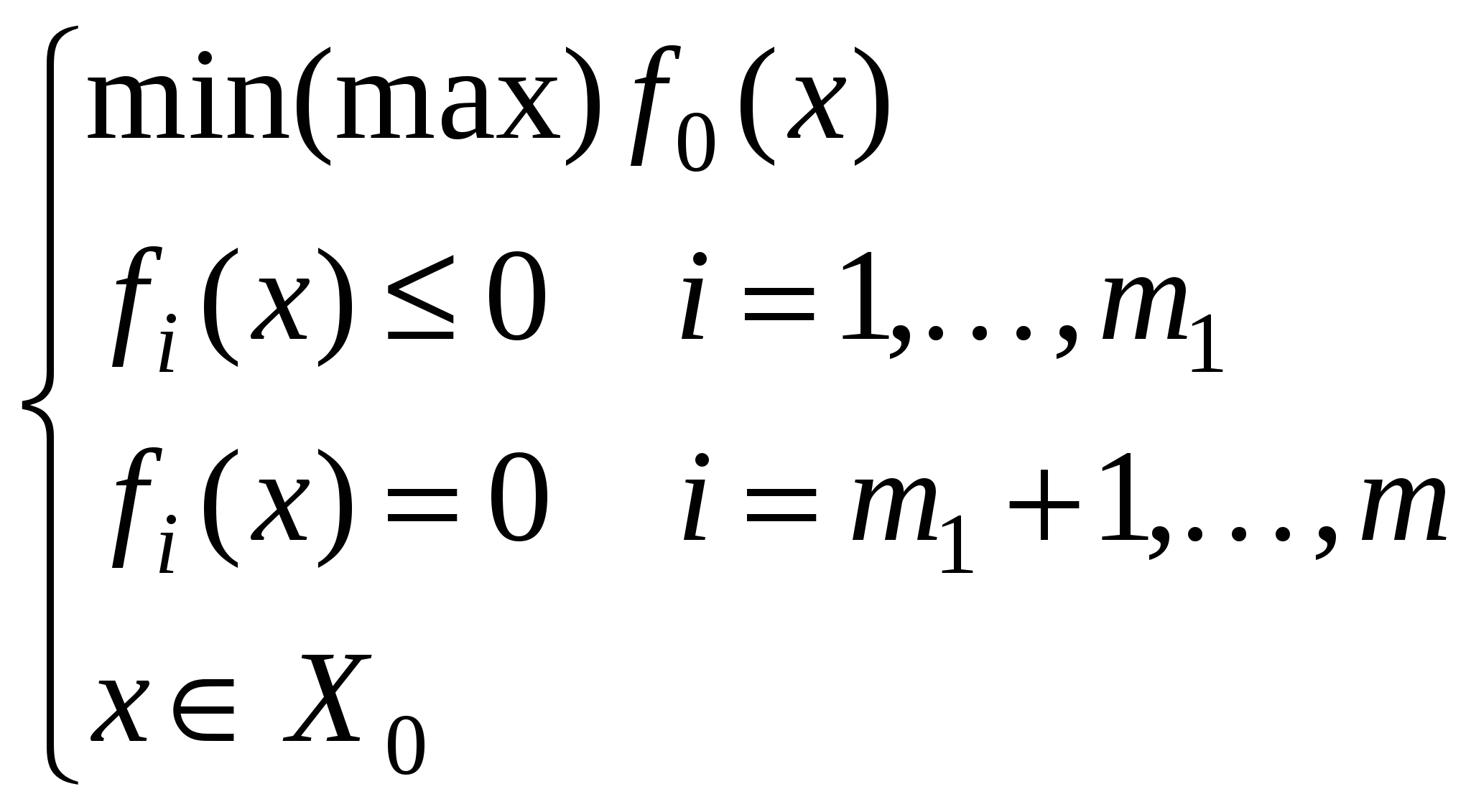- функции от n переменных (т.е x – это n-мерный вектор)

В частности, стандартная задача линейного программирования: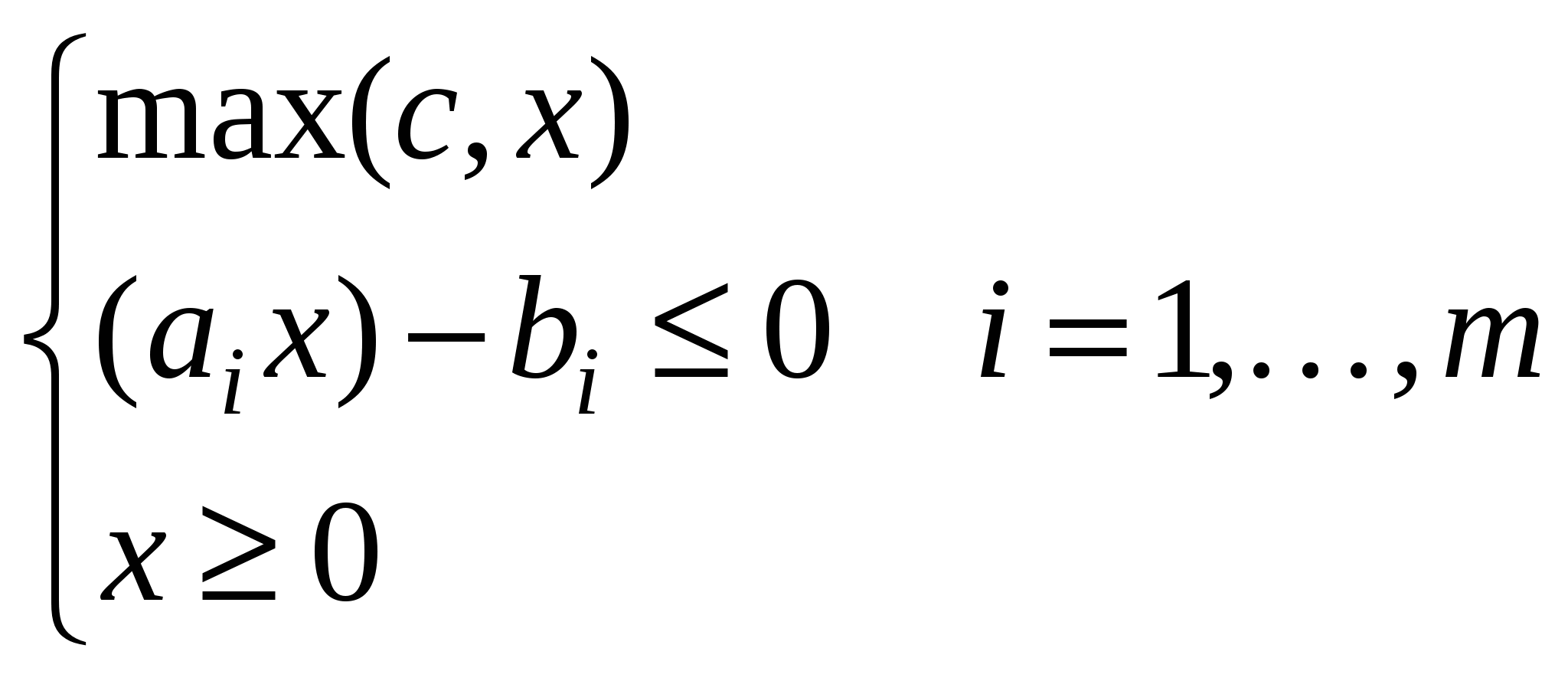

2. 
   Сетевое планирование и управление – построение сетевых моделей и решения задач на этих моделях.
   
3. 
   Теория массового обслуживания (теория очередей) – трактуют процесс производства как процесс выполнения заявок.
   
4. 
   Теория расписания.
   
5. 
   Экономические приложения теории игр.
   

IV. Экономическая кибернетика

Наука о наиболее общих принципах управления экономическими процессами (с целью принятия оптимальных решений).

1. 
   Системный анализ в экономике.
   
2. 
   Теория экономической информации.
   
3. 
   Теория управляющих систем, в частности теория АСУ
   

V. Экспериментальные методы в экономике

1. 
   Математическая теория планирования эксперимента.
   

1-минимизировать вмешательство в систему в активной проверке модели;

2-повысить качество эксперимента.

2. 
   Имитационное моделирование.
   
3. 
   Деловые игры, обучающие системы
   

7. 
   Этапы экономико-математического моделирования.
   

Этапы:

1. 
   Постановка задачи (экономической) – даётся содержательное описание объекта или процесса
   
2. 
   Возникает математическая модель экономической задачи.
   
3. 
   Математический анализ модели.
   
4. 
   Информационное наполнение задачи (a, b, c – заменить на числа, реального производства). Можно получить неверную информацию или не получить вообще. В этом случае в качестве информации можно использовать статистические данные (новая модель в модели – может понадобиться построение вспомогательных математических моделей) или вымышленные.
   
5. 
   Численное решение задачи – выбрать алгоритм решения, написать программу, провести численный эксперимент (запустить программу).
   
6. 
   Применение решения.
   

8. 
   Связь математического моделирования с экономической теорией и практикой.
   

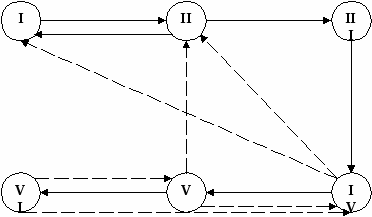
С теорией:

1. 
   Терминология (производная и т.п.) – математика дает удобную систему обозначений экономистам.
   
2. 
   Многие экономические понятия являются трактовкой математических терминов и определений (предельный эффект = производная, теневые цены: множитель Лагранжа, двойственные оценки в задаче линейного программирования)
   
3. 
   Математика интенсифицирует экономическую теорию (за счёт математического анализа, имитационного анализа)
   
4. 
   Экономика, как и математика, использует аксиомы (аксиоматический метод).
   

С практикой:

1. 
   Математика упорядочивает систему экономической информации (используются модели мат.статистики)
   
2. 
   Интенсифицирует экономические расчёты.
   
3. 
   Математика решает новые экономические задачи (например, задачи прогноза), даёт новые методы решения задач.
   
4. 
   Развивает количественный анализ параметров экономической теории.
   

9. 
   Линейные модели:
   

1. 
   задача планирования производства
   

Имеется некоторое абстрактное производство, использующее n видов ресурсов, перерабатывающее их в конечный продукт.

Постановка задачи, 1-ый вариант:

Внутренние параметры модели (вектор a):

m ресурсов.

b_i – объем i-го ресурса
n технологий (производственных способов)
а_ij – затраты i-го ресурса при использовании j-ой технологии с единичной интенсивностью
c_j – ценность конечной продукции, вырабатываемой j-ой технологией в единицу времени.

Требуется, не выходя за рамки отпущенных ресурсов так спланировать производство, чтобы получить максимальную суммарную ценность.

x_j – искомая интенсивность использования j-ой технологии. x = (x₁, …, x_n)
2-й вариант:

m ресурсов.

b_i – объем i-го ресурса
n видов продуктов
а_ij – расход i-го ресурса на производство одной единицы j-го продукта
c_j – прибыль, получаемая от производства одной единицы j-го продукта

x_j – искомое количество j-го продукта
Модель:

– максимизировать ценность (прибыль)

– использование i-го ресурса

2. 
   задача диеты
   

Живые организмы должны получать за определённое время некоторое количество веществ.

m биологически активных веществ.
b_i – количество i-го вещества, потребляемого организмом в планируемом периоде.
n продуктов питания
a_ij – содержание i-го вещества в одной единице веса j-го продукта.
c_j – цена единицы j-го продукта

Требуется так выбрать диету, чтобы удовлетворить потребности организма в веществах по возможности самым дешёвым образом.

x_j – искомое количество покупки j-го продукта.
Модель:

– минимизировать стоимость

– потребление i-го вещества

3. 
   транспортная задача
   

m пунктов производства однородной продукции
a_i – объём производства в i-ом пункте производства
n пунктов потребления продукта
b_j – объём потребностей j-го потребителя
c_ij – стоимость перевозки 1-цы груза с i-го пункта производства в j-ый пункт потребления
Требуется так организовать перевозку, чтобы полностью вывезти продукт из каждого пункта производства, полностью удовлетворить потребности каждого потребителя и минимизировать при этом суммарные транспортные издержки. (Считается, что суммарный объём производства равен суммарному объёму потребления).

x_ij – искомый объём перевозки из i-го пункта производства в j-ый пункт потребления

Модель:

– минимизировать стоимость перевозки

– вывести из каждого пункта производства всю продукцию

– полностью удовлетворить потребности каждого потребителя



m + n ограничений и m·n переменных.

Если поменяем индексы (i,j)→(k) (вытянем матрицу в вектор), то модель будет выглядеть:

x = (x₁, …, x_m·n)



, либо 0, либо 1