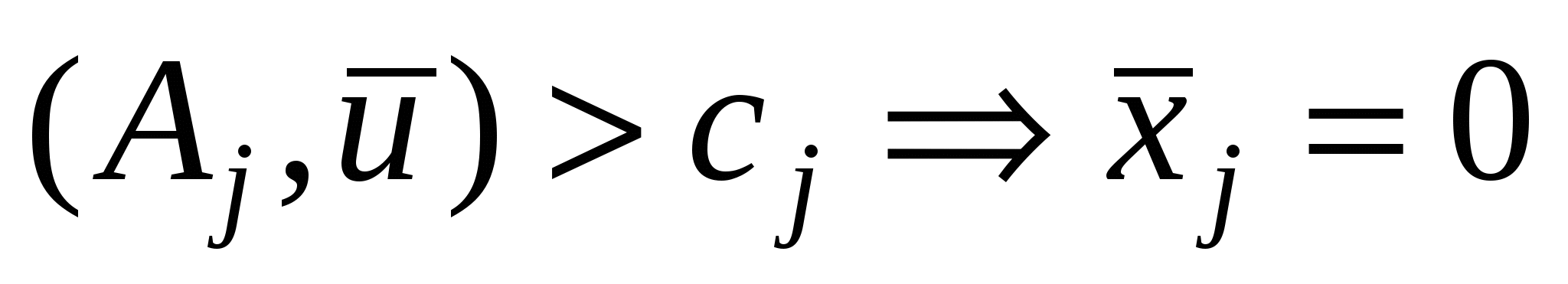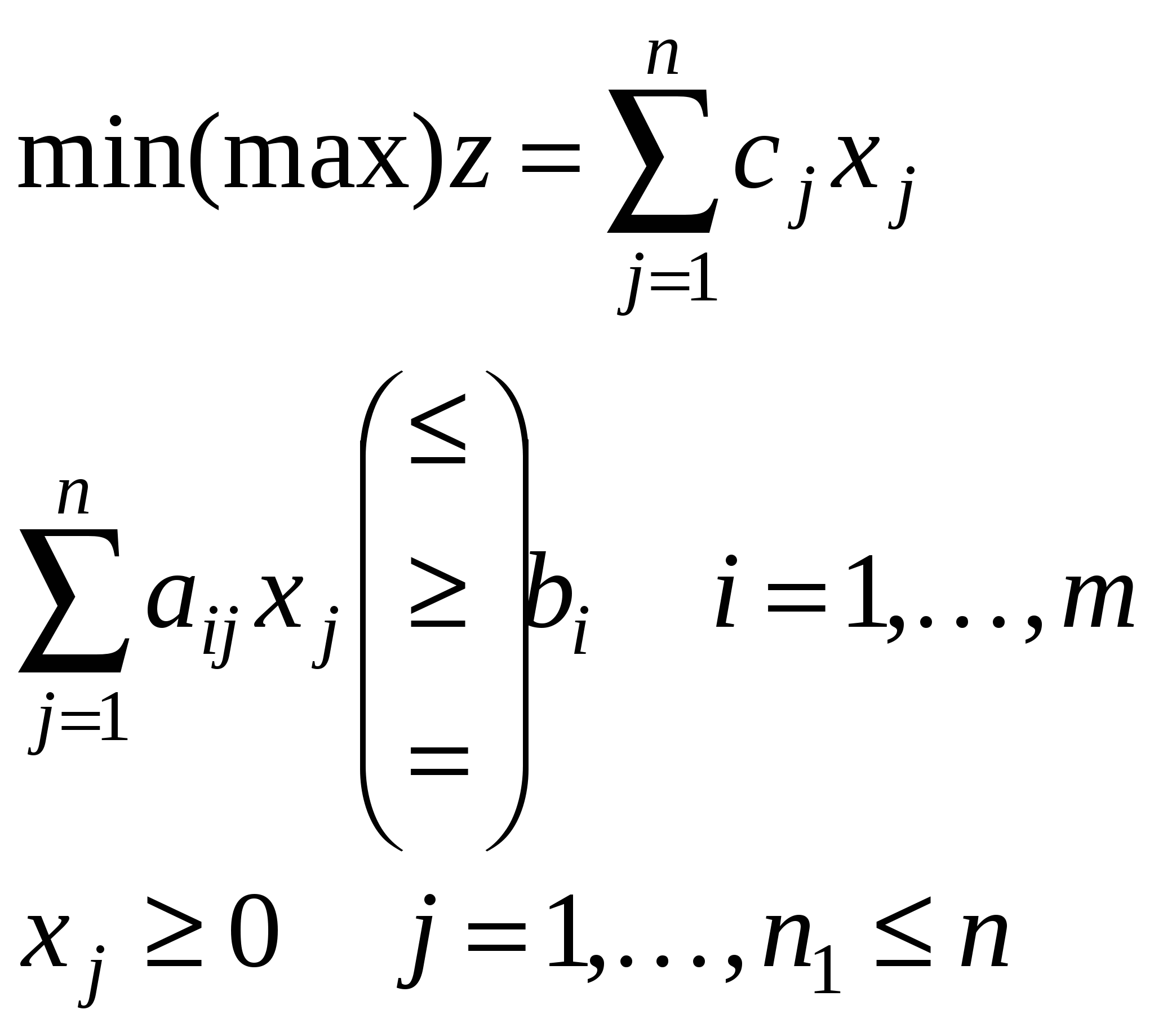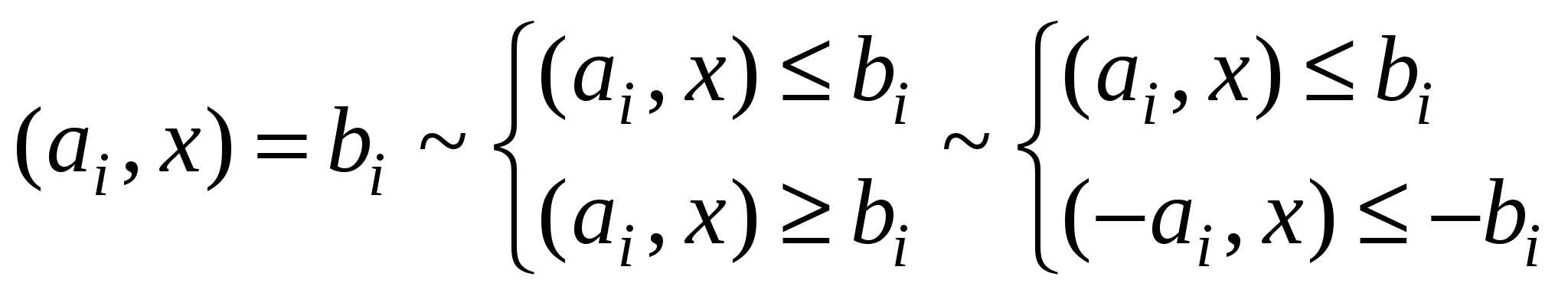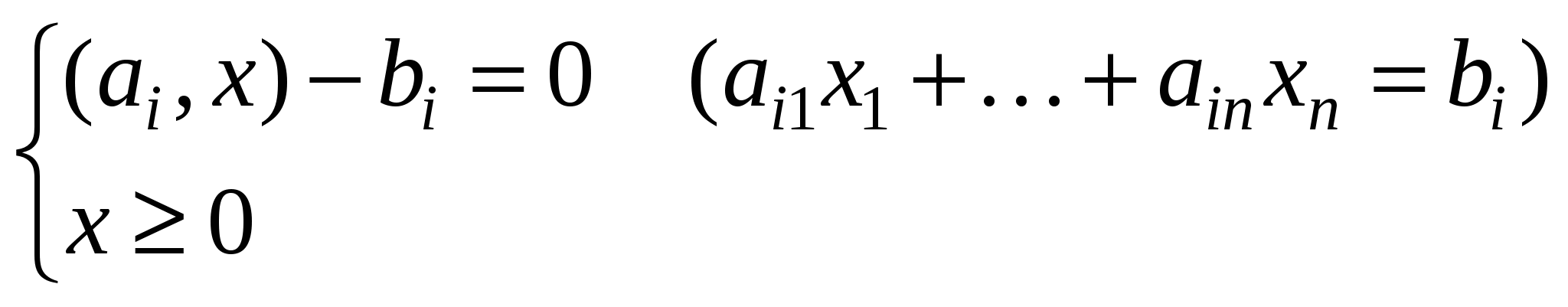Ответы по ЭММ(прошлогодние). 2011г. История возникновения экономикоматематических методов (эмм)

• Название: 2011г. История возникновения экономикоматематических методов (эмм)
• Анкор: Ответы по ЭММ(прошлогодние).doc
• Дата: 04.07.2018
• Размер: 0.5 Mb.
• Имя файла: Ответы по ЭММ(прошлогодние).doc
• Тип: Документы; #21057
• страница: 2 из 3

Различные виды моделей линейного программирования (ЛП), их эквивалентность.

I. Общая задача ЛП


z – целевая функция

c = (c₁, …, c_n) – вектор целей

A = (a_ij)_mxn – матрица задачи (матрица условий)

b = (b₁, …, b_m) – вектор ограничений (вектор правых условий)

x = (x₁, …, x_n) – план задачи (решение задачи)

Условие x_j ≥ 0 – условие неотрицательности переменных
Множество x, удовлетворяющих всем ограничениям называется множеством допустимых решений, обозначается X. План, на котором достигается оптимум целевой функции (минимум/максимум) называется решением задачи (оптимальный план), обозначается x^*. X^* – множество решений задачи.

Решить общую задачу ЛП означает, найти хотя бы один оптимальный план и вычислить оптимальное значение.

Частные задачи ЛП

Скалярная форма	Матричная форма	Векторная форма
II. Стандартная задача ЛП (задача планирования производства)
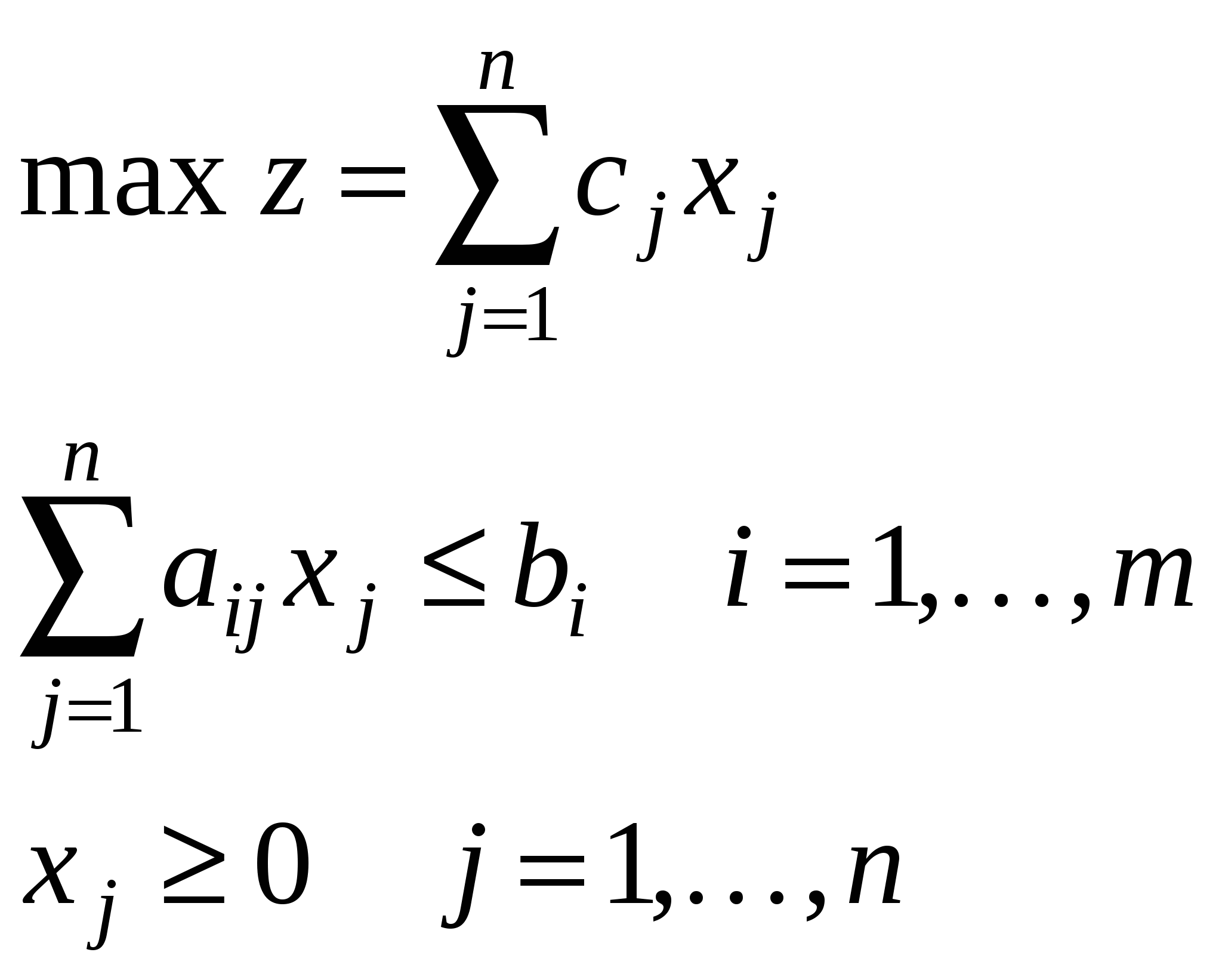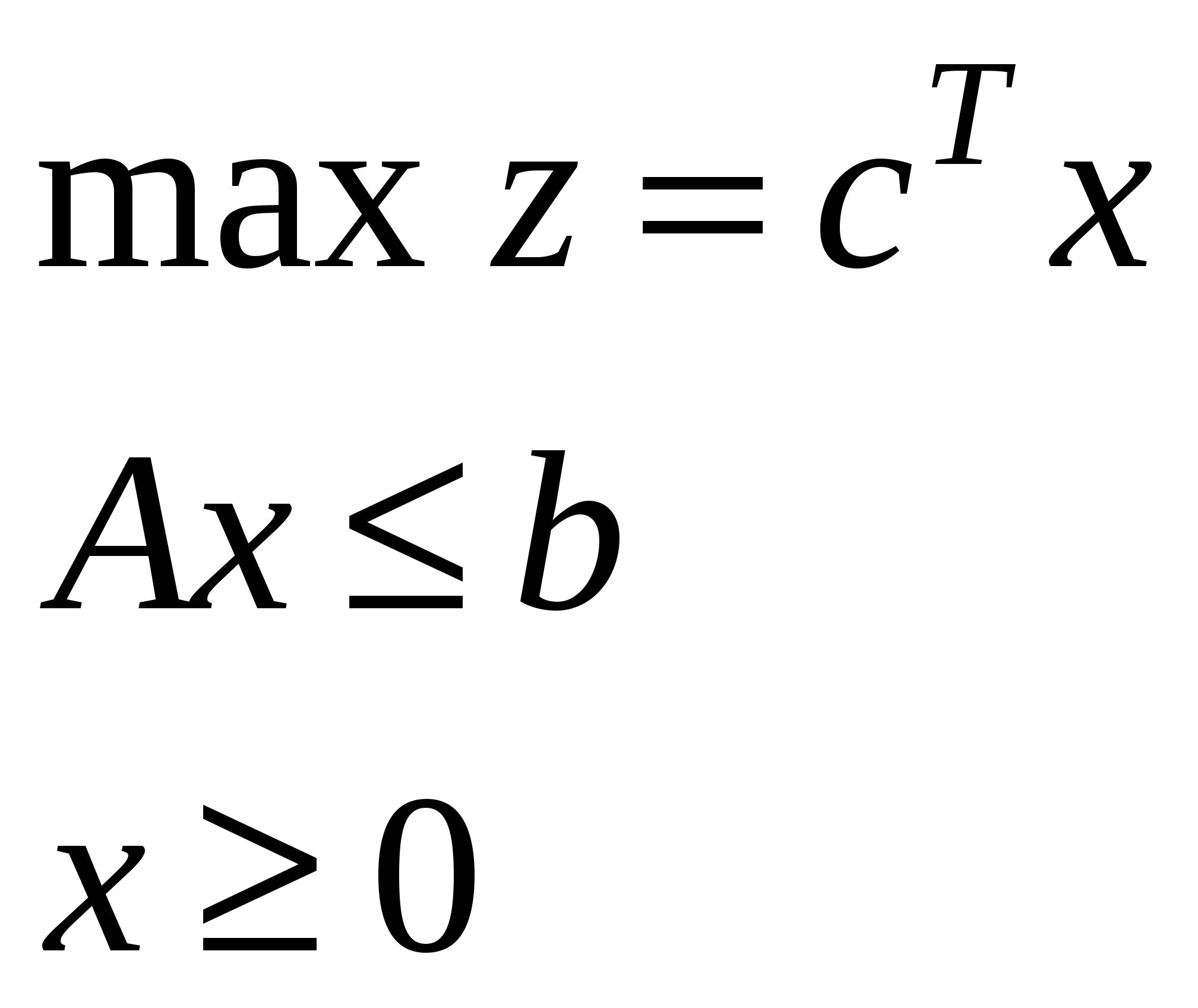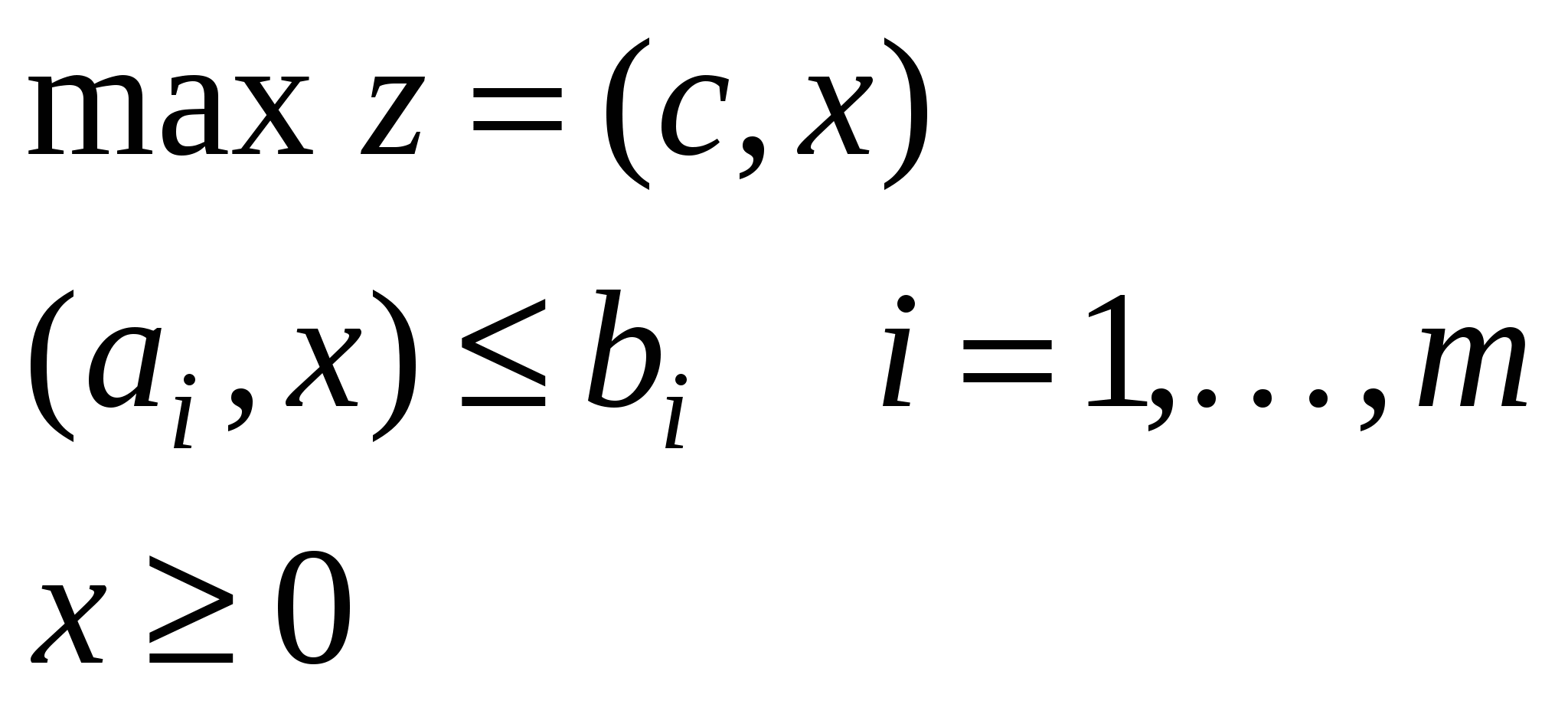III. Каноническая задача ЛП (транспортная задача)
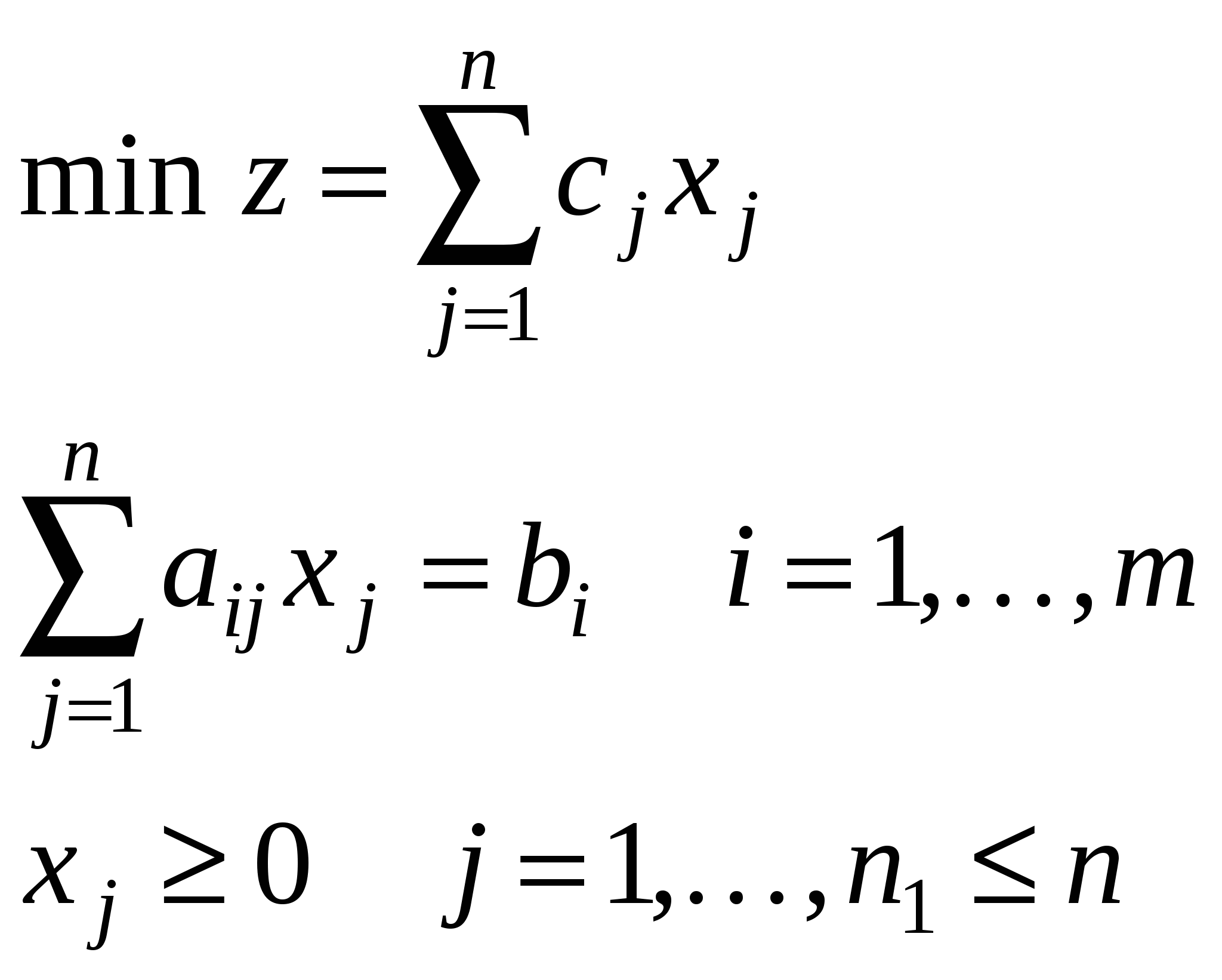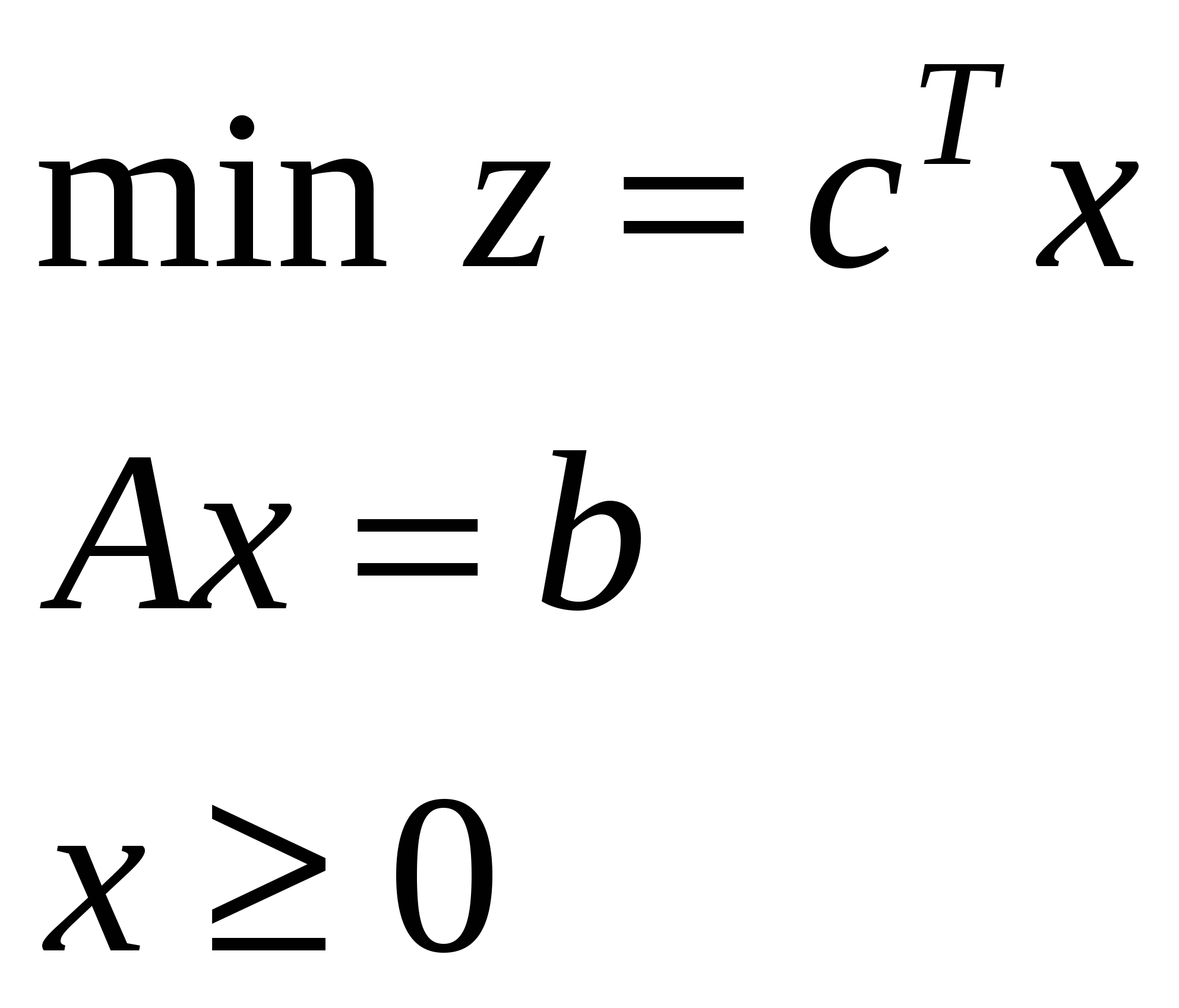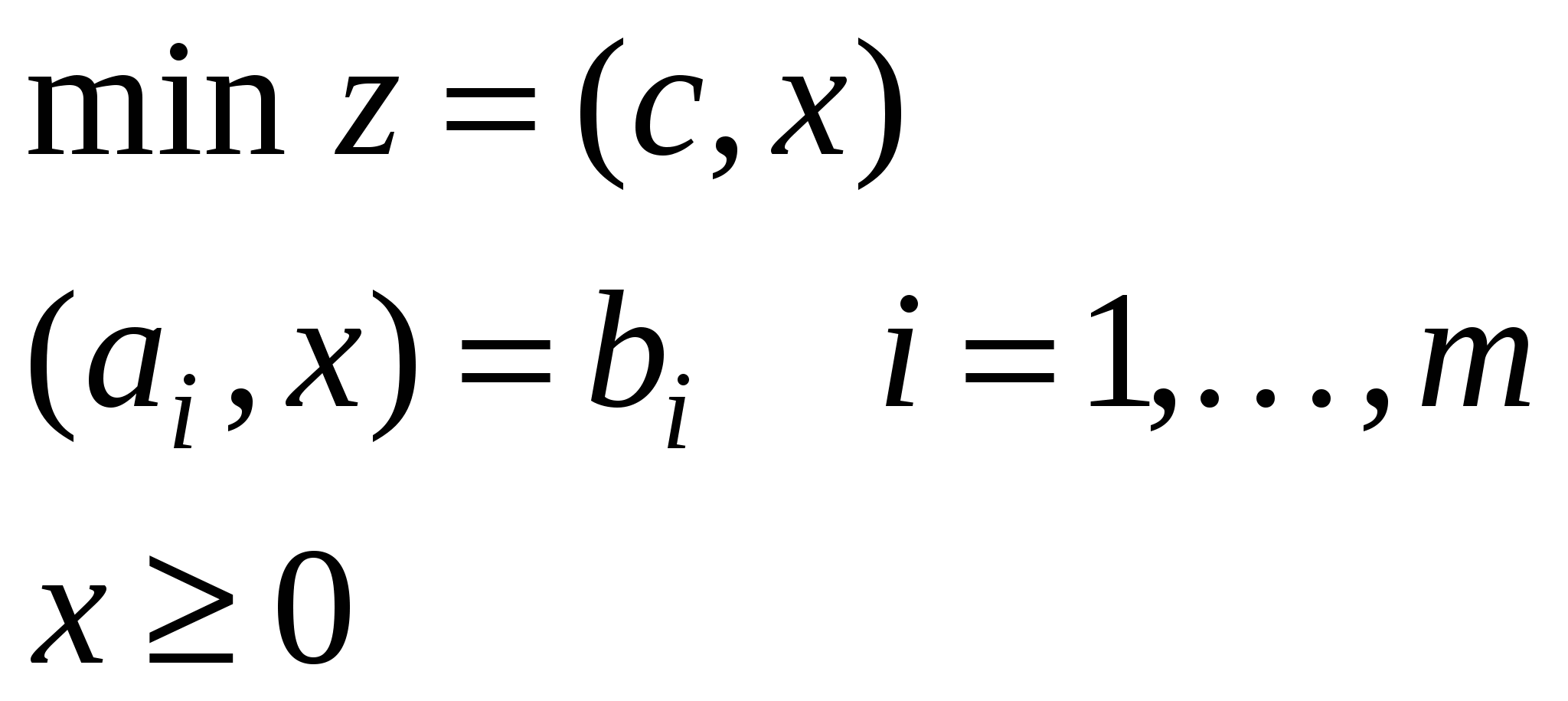IV. Основная задача ЛП

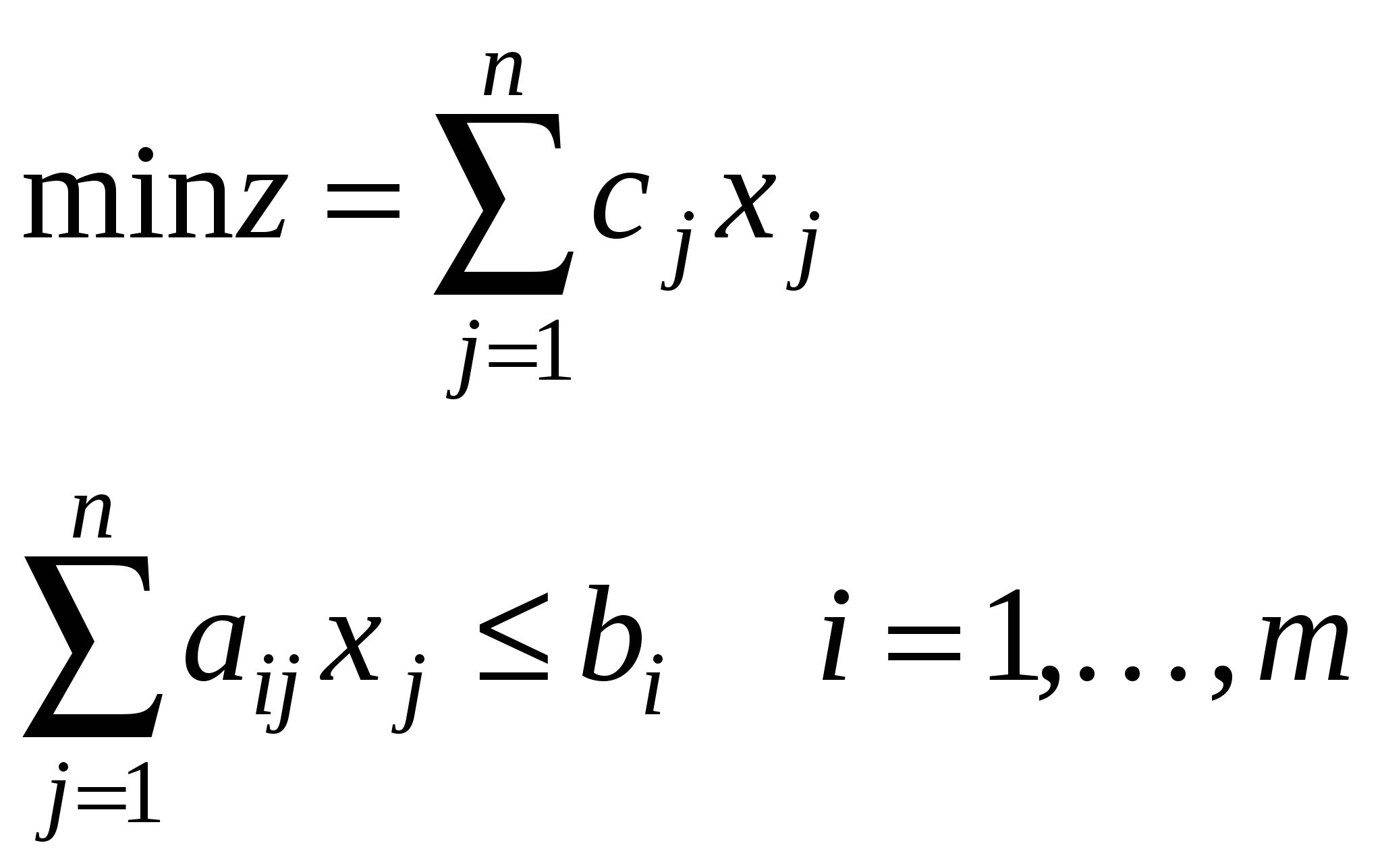Все виды задач ЛП эквивалентны: существуют однозначные правила перехода от одного вида задачи к другому и решая последнюю задачу и вспоминая правила перехода, мы можем написать решение исходной задачи, не решая ее.
Правила перехода

1. 
   
   

2. 
   
   

3. 
   
   

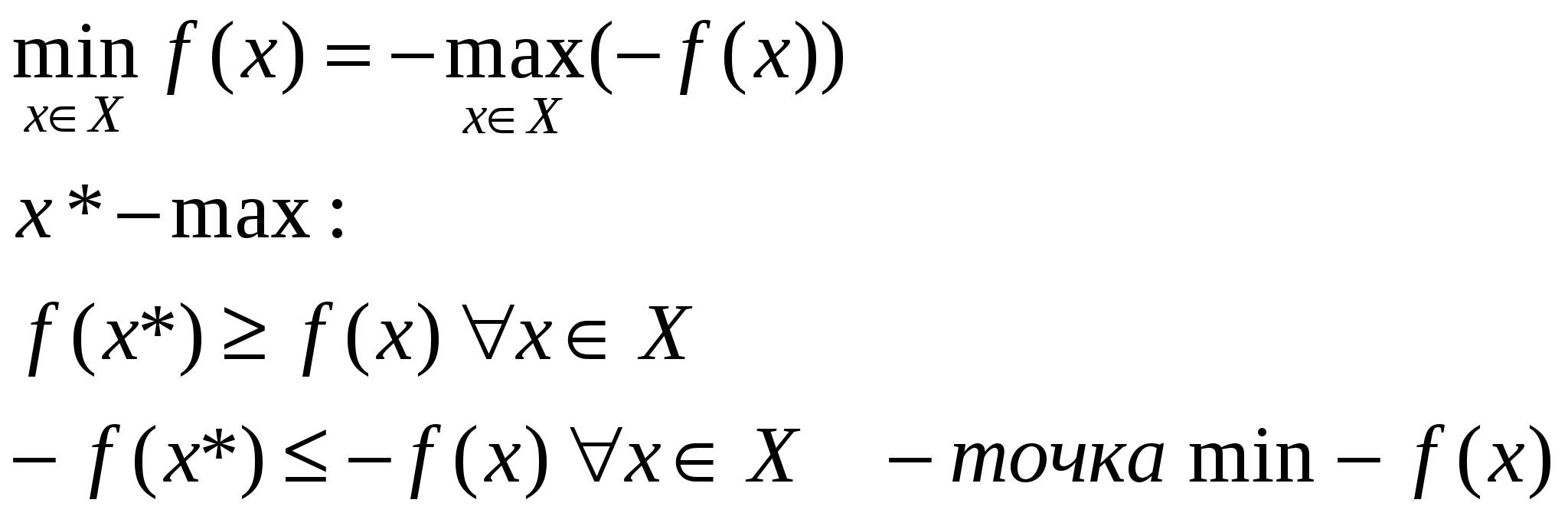
x_n+i – дополнительные переменные, (насколько недоиспользовано ограничение)

4. 
   
   

5. 
   
   

Пусть a_i1 ≠ 0

6. 
   Пусть
   

7.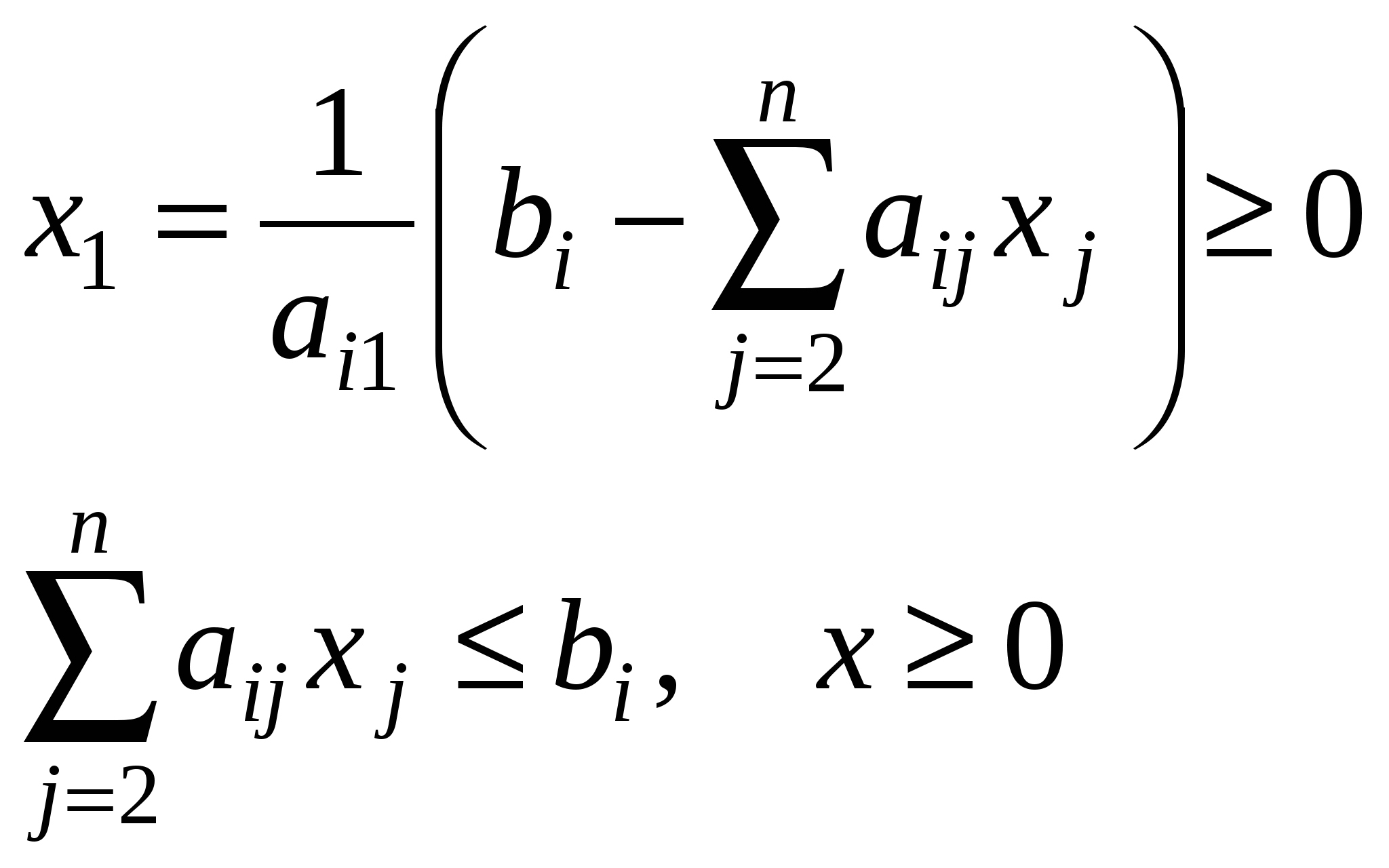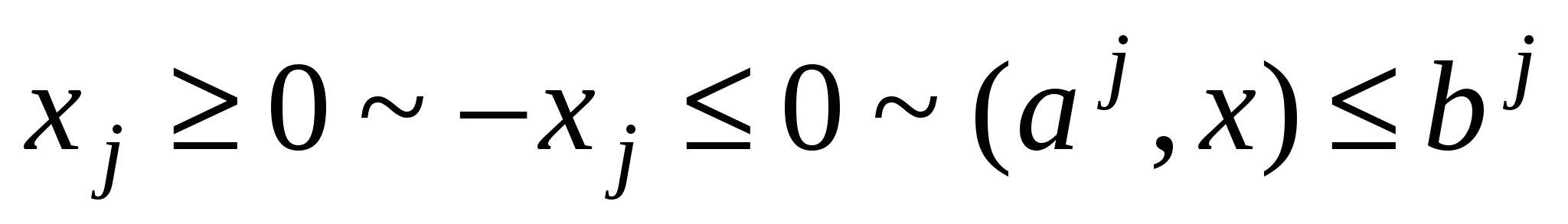 
   Пусть x_j – свободная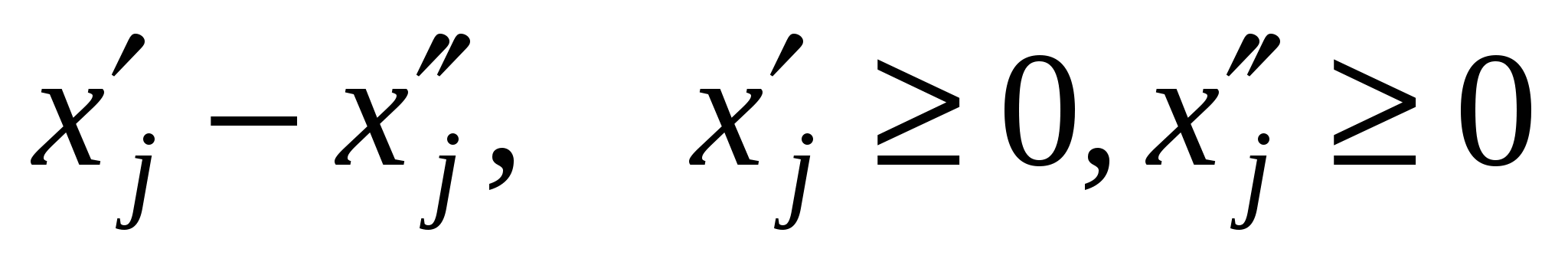

– любую свободную переменную можно представить в виде разности двух неотрицательных переменных.

11. 
    Г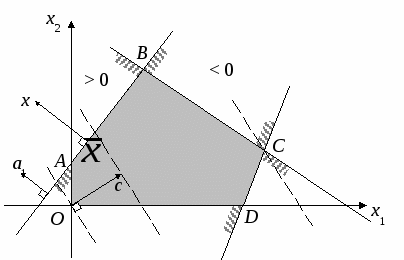рафический анализ линейных моделей.
    

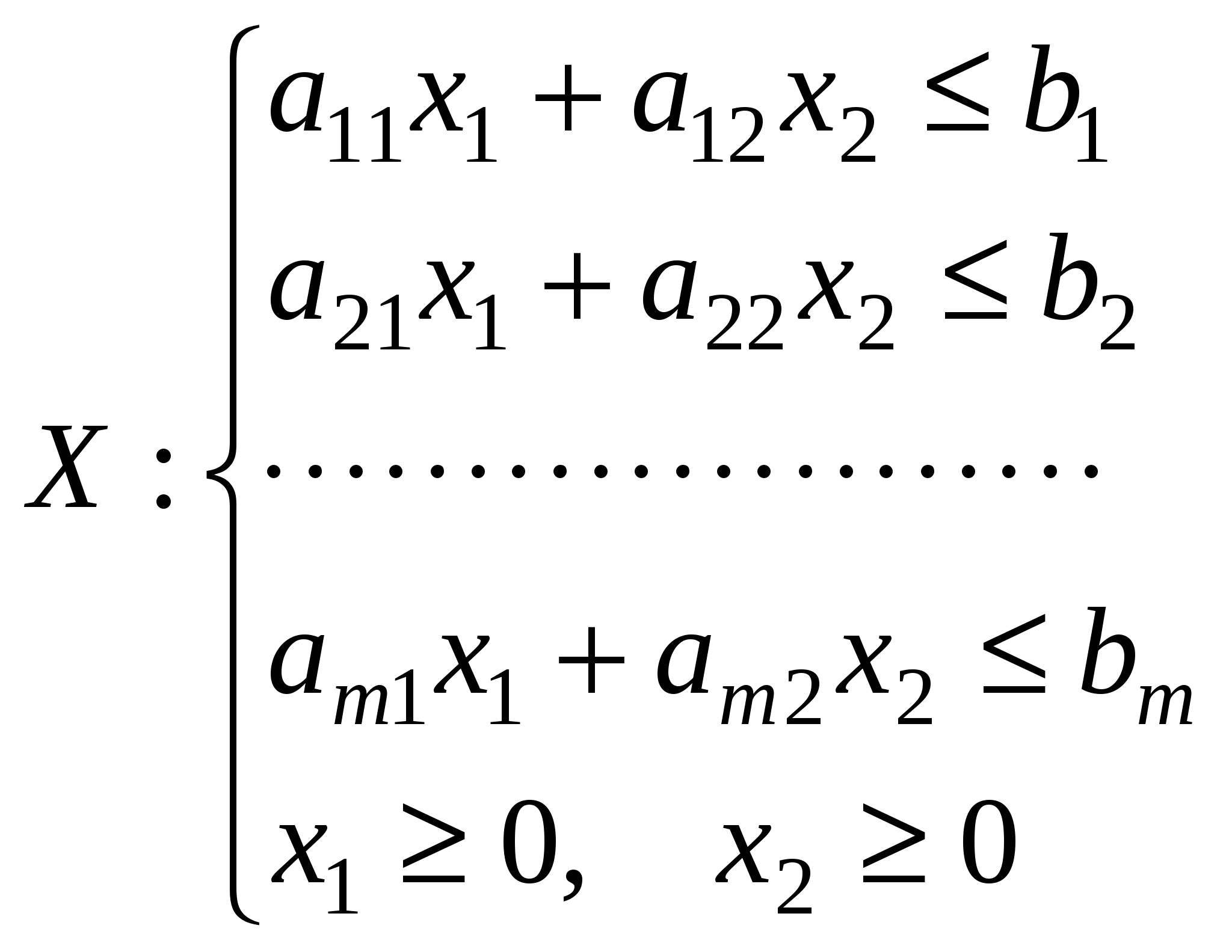
m = 3

1. 
   Строим границы множества решений, которые соответствуют неравенствам (прямые: )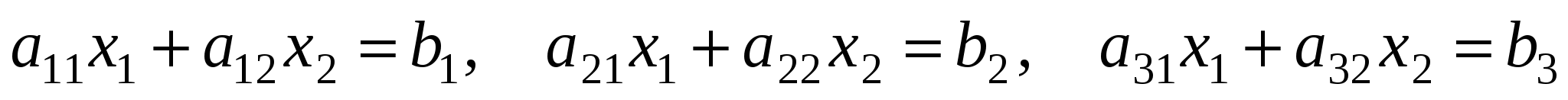
   
2. 
   Находим полуплоскости, соответствующие каждому ограничению (метод пробной точки)
   

3. 
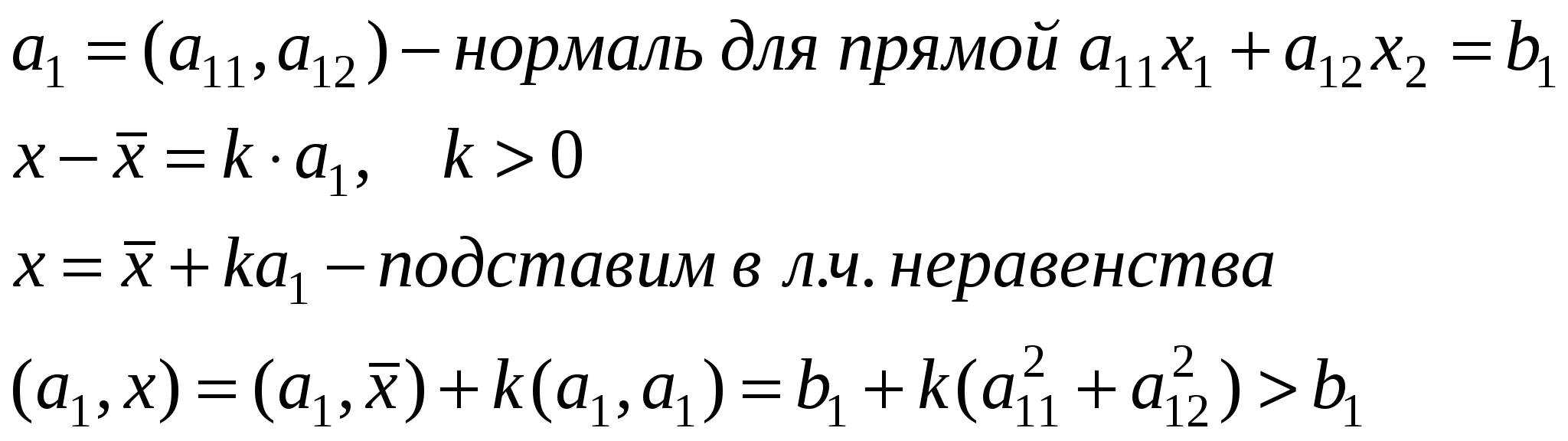
   Находим многоугольник допустимых решений, как пересечение найденных полуплоскостей. Полученную область заштриховать. Возможные варианты:
   
   1. 
      X – многоугольник
      
   2. 
      X – пустое множество
      
   3. 
      X – неограниченное многоугольное множество
      
4. 
   Находим координаты вектора градиента целевой функции (вектор целей – вектор нормали к линиям уровня)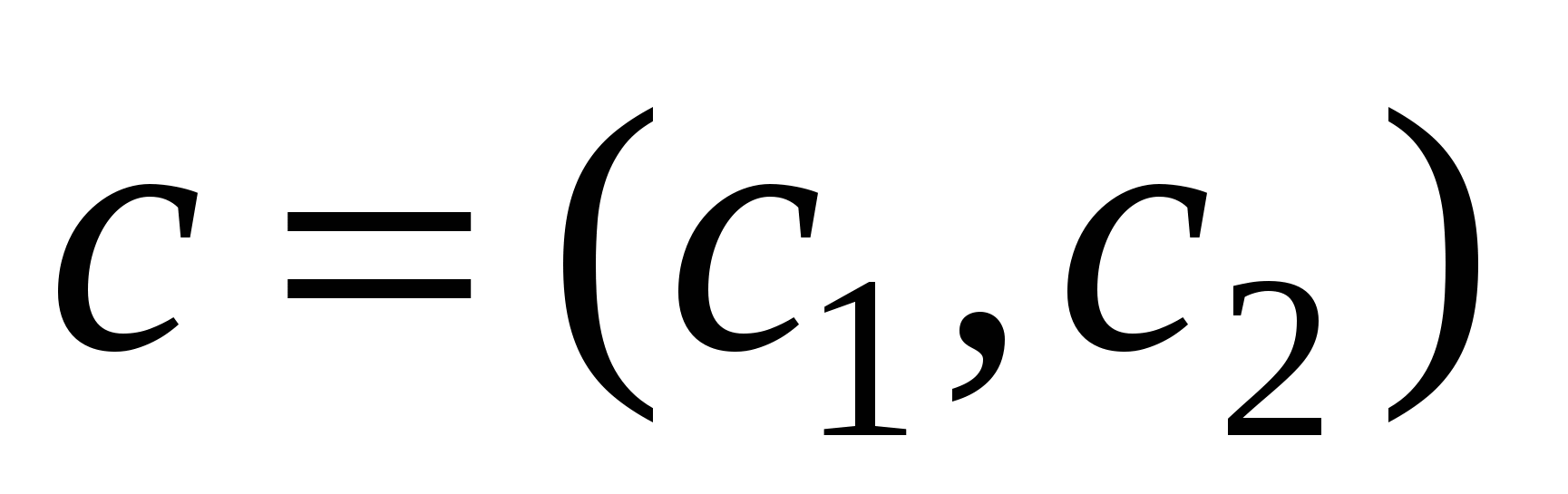
   
5. 
   Строим прямую (перпендикулярно вектору цели), которая соответствует линии уровня для z₀ = 0.
   

Затем перемещаем прямую в направлении вектора цели (в случае задачи на min – в противоположном направлении) до тех пор, пока прямая имеет общие точки с множеством допустимых решений. Крайнее положение – ответ.

6. 
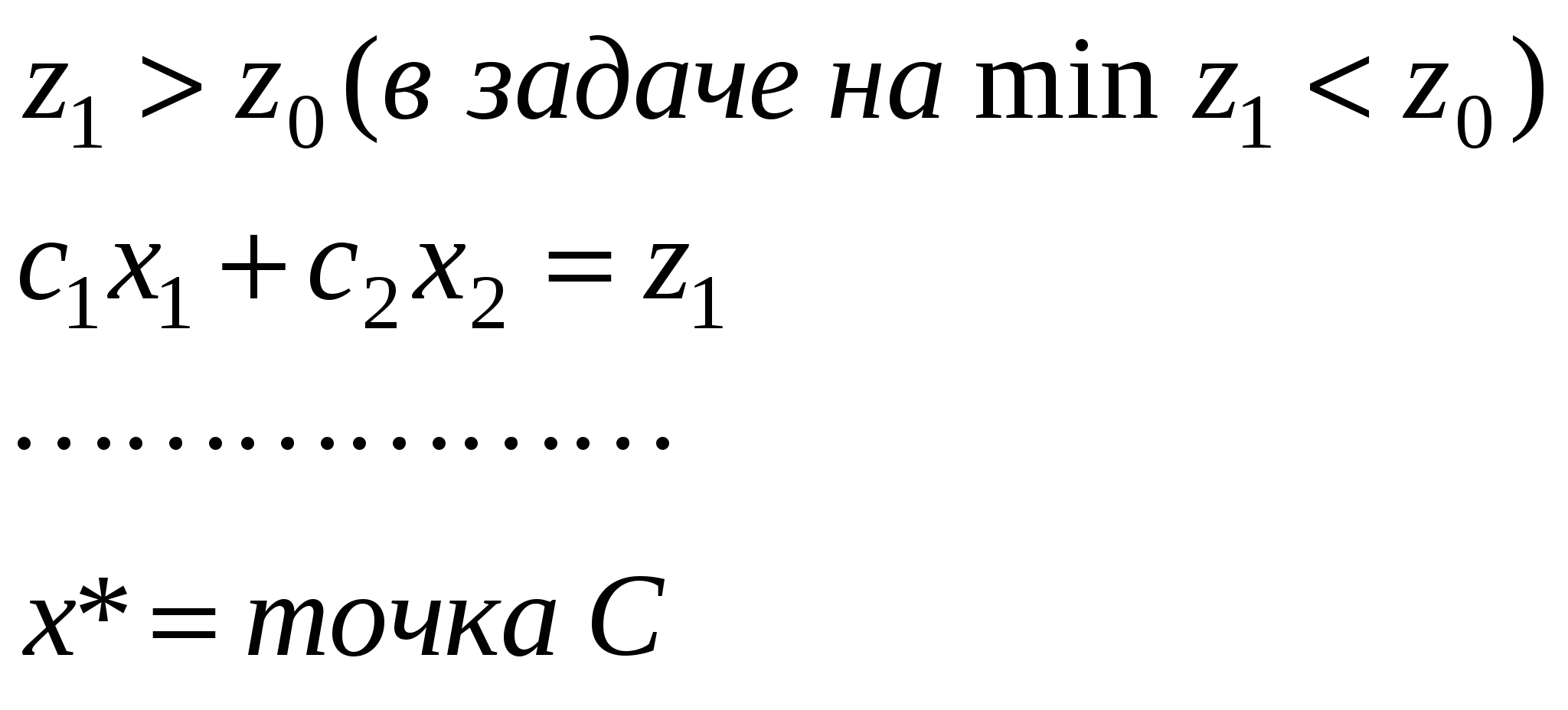
   Вычисляем координаты крайней точки, как пересечение соответствующих прямых и вычисляем значение целевой функции в этой точке.
   

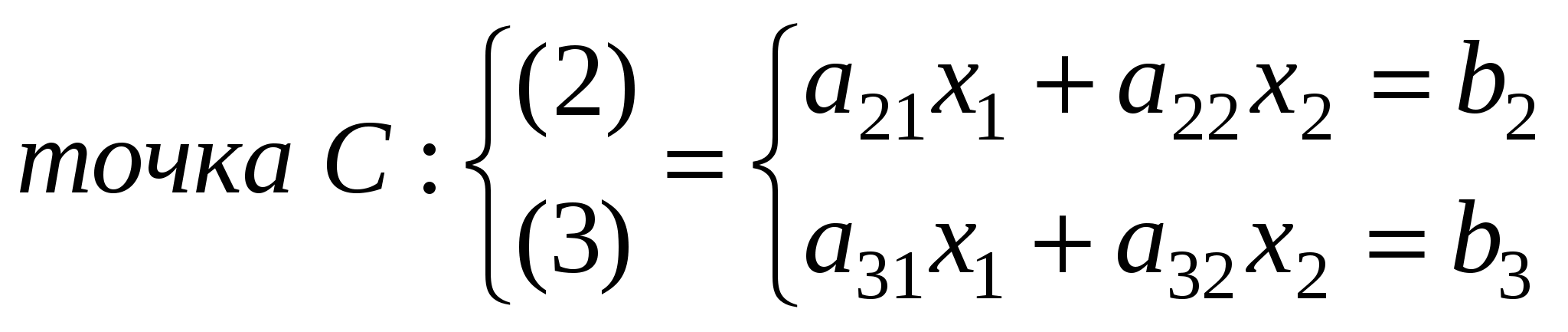
Ответ:

12. 
    Двойственные модели ЛП, их экономическая интерпретация.
    

Рассмотрим задачу L планирования производства (1-ый вариант).

Скалярная форма	Матричная форма	Векторная форма

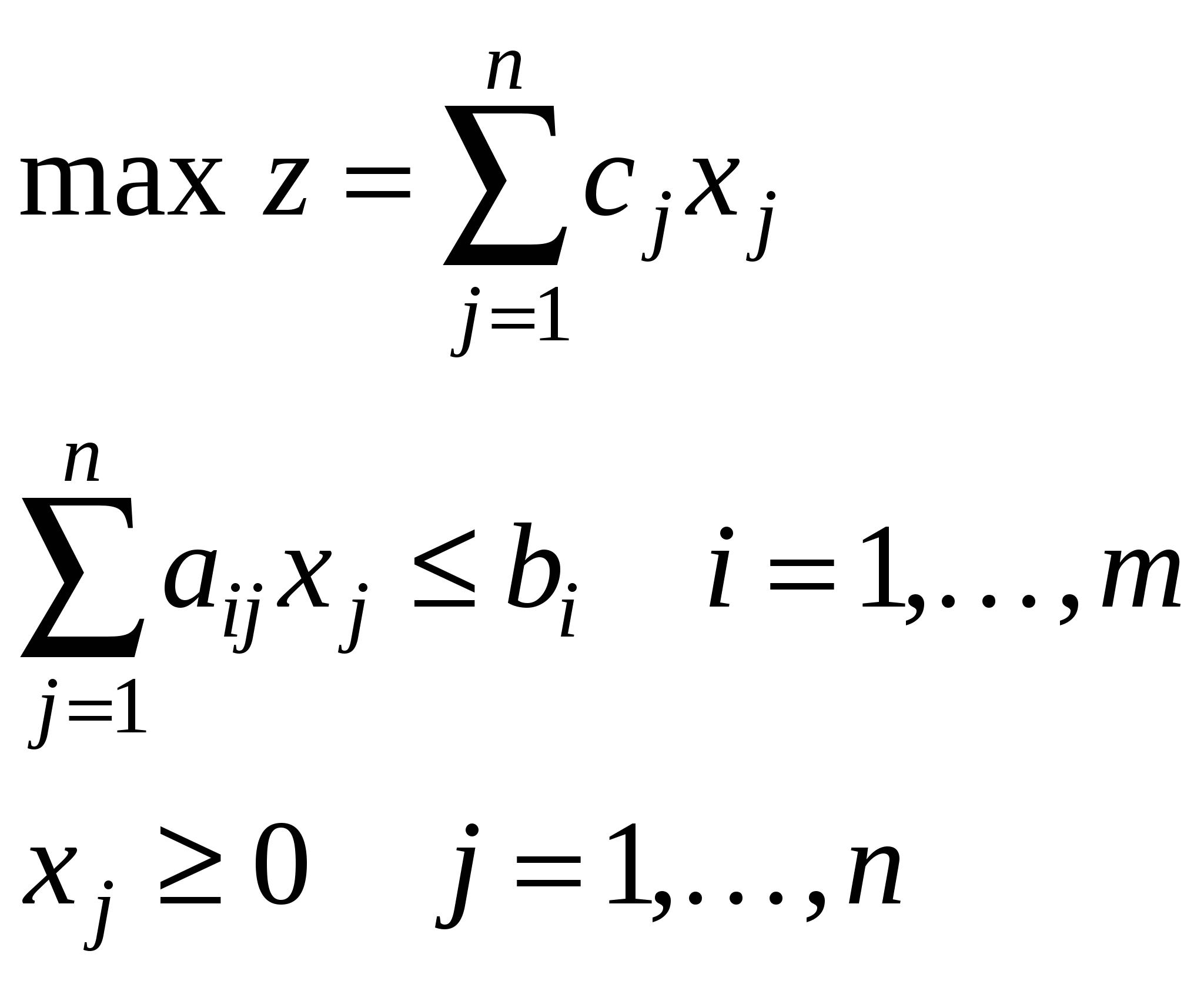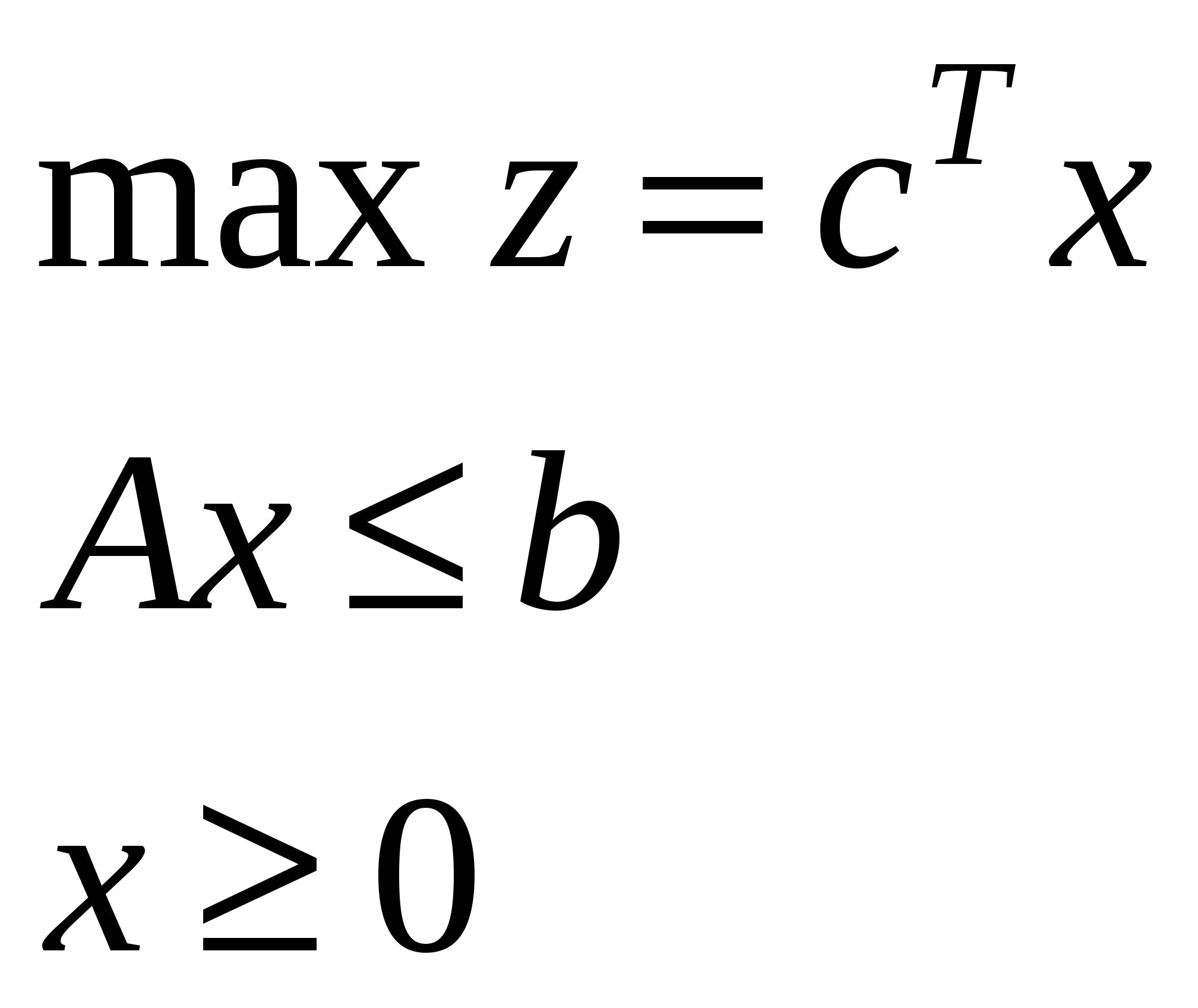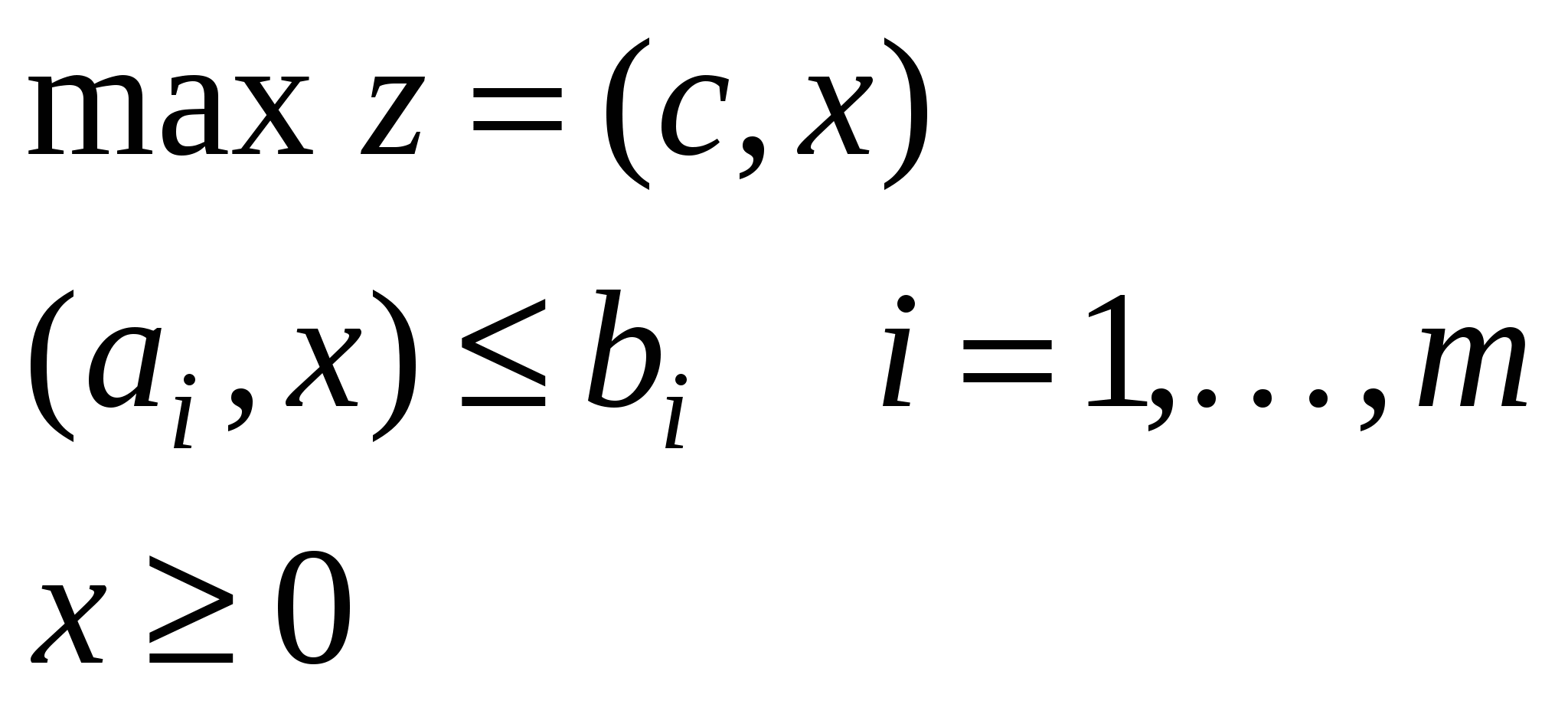m ресурсов.

b_i – объем i-го ресурса
n технологий
а_ij – затраты i-го ресурса при использовании j-ой технологии в единицу времени
c_j – получаемая ценность при использовании j-ой технологии в единицу времени

x_j – время работы j-ой технологии.

x = (x₁, …, x_n)
Оценим ценность затраченную и полученную в единицу времени

u_i – ценность единицы i-го ресурса

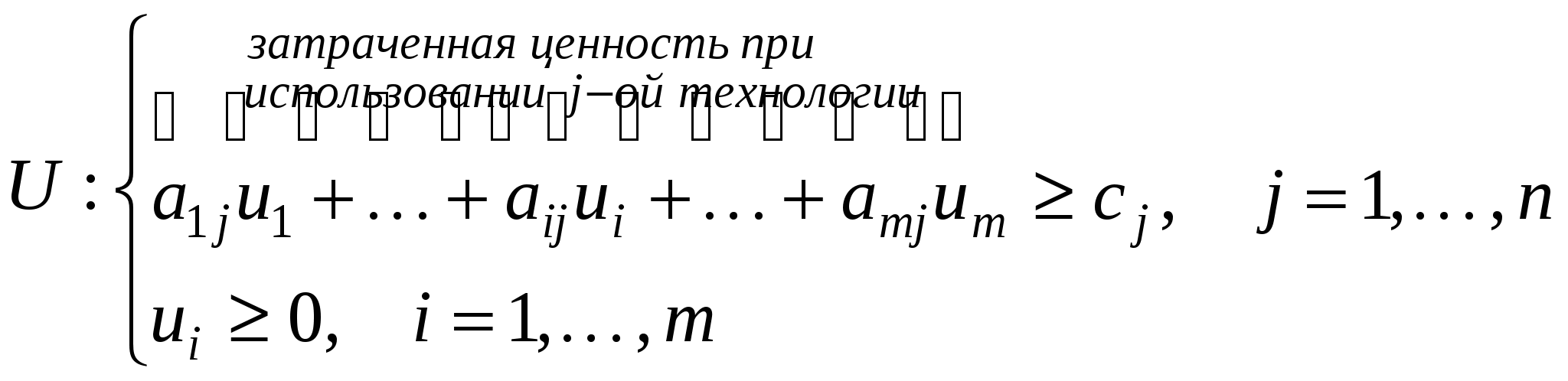
Скалярная форма	Матричная форма	Векторная форма

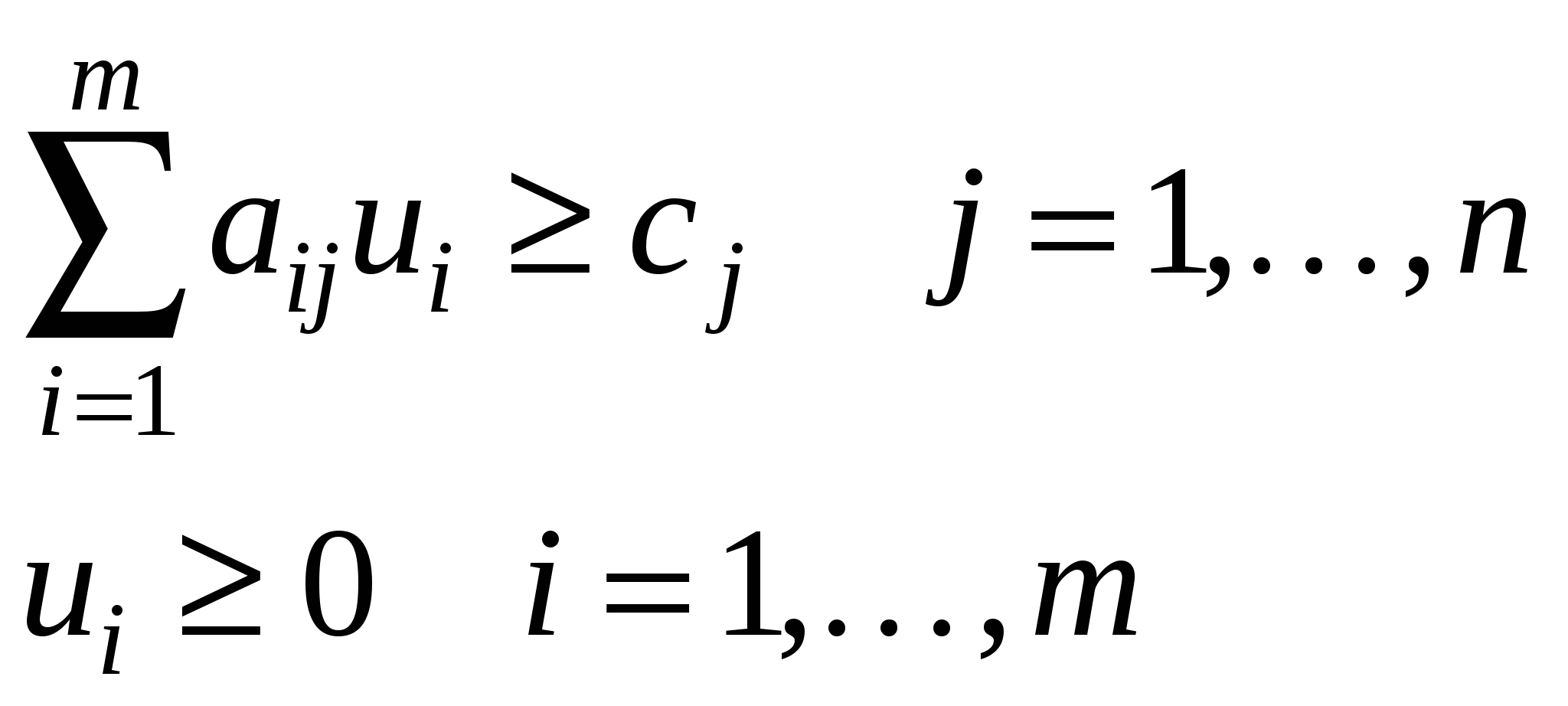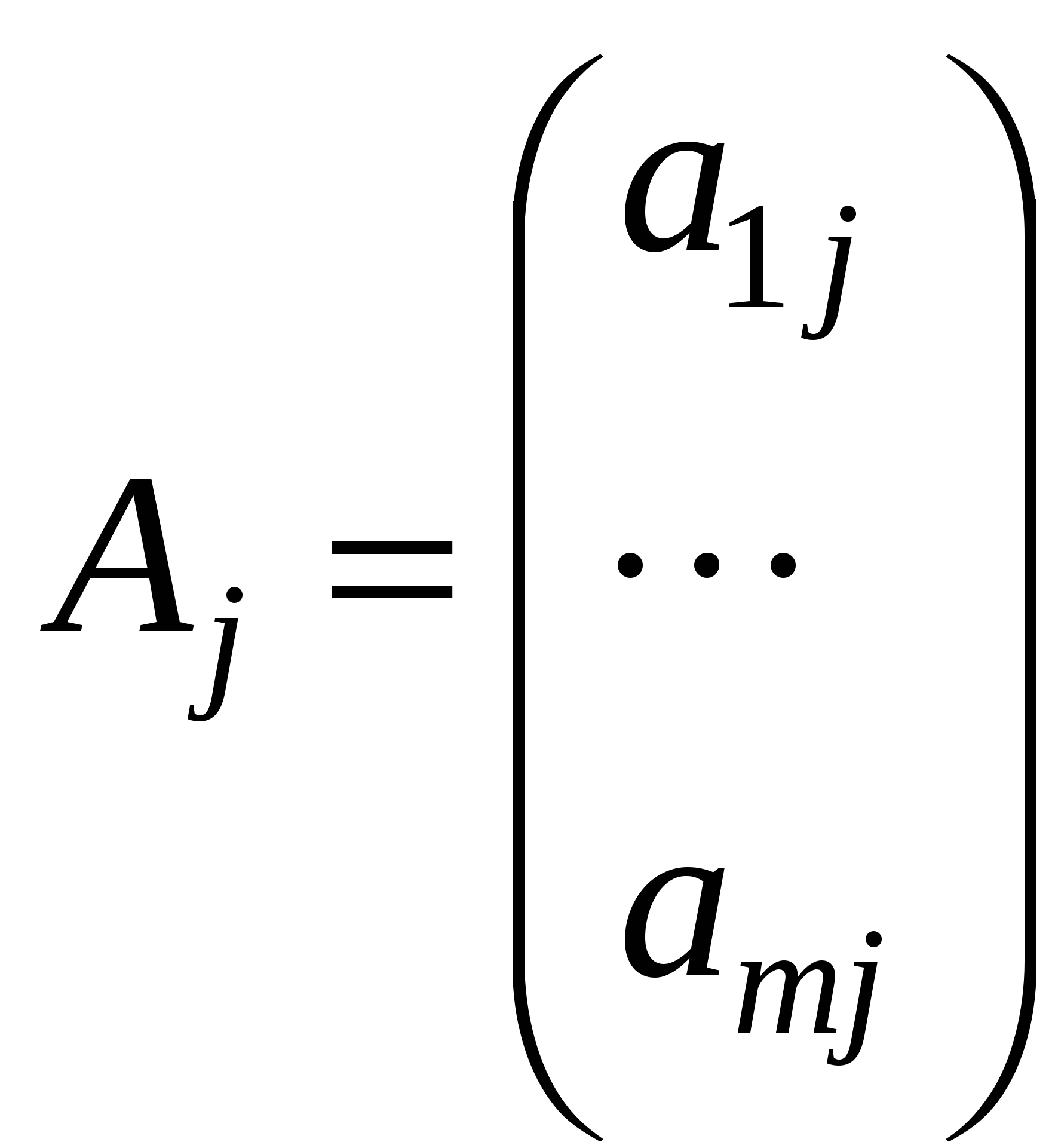Δ – потери

x – план производства






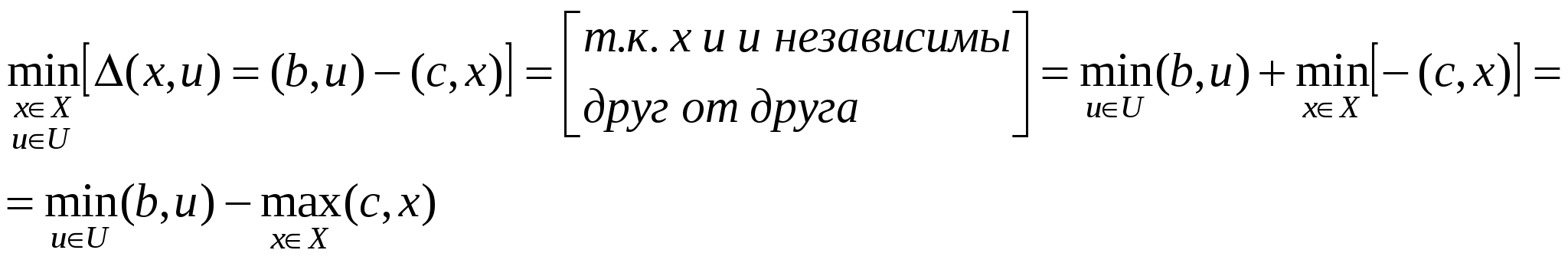
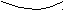
L*– двойственная задача к задаче L

Скалярная форма	Матричная форма	Векторная форма

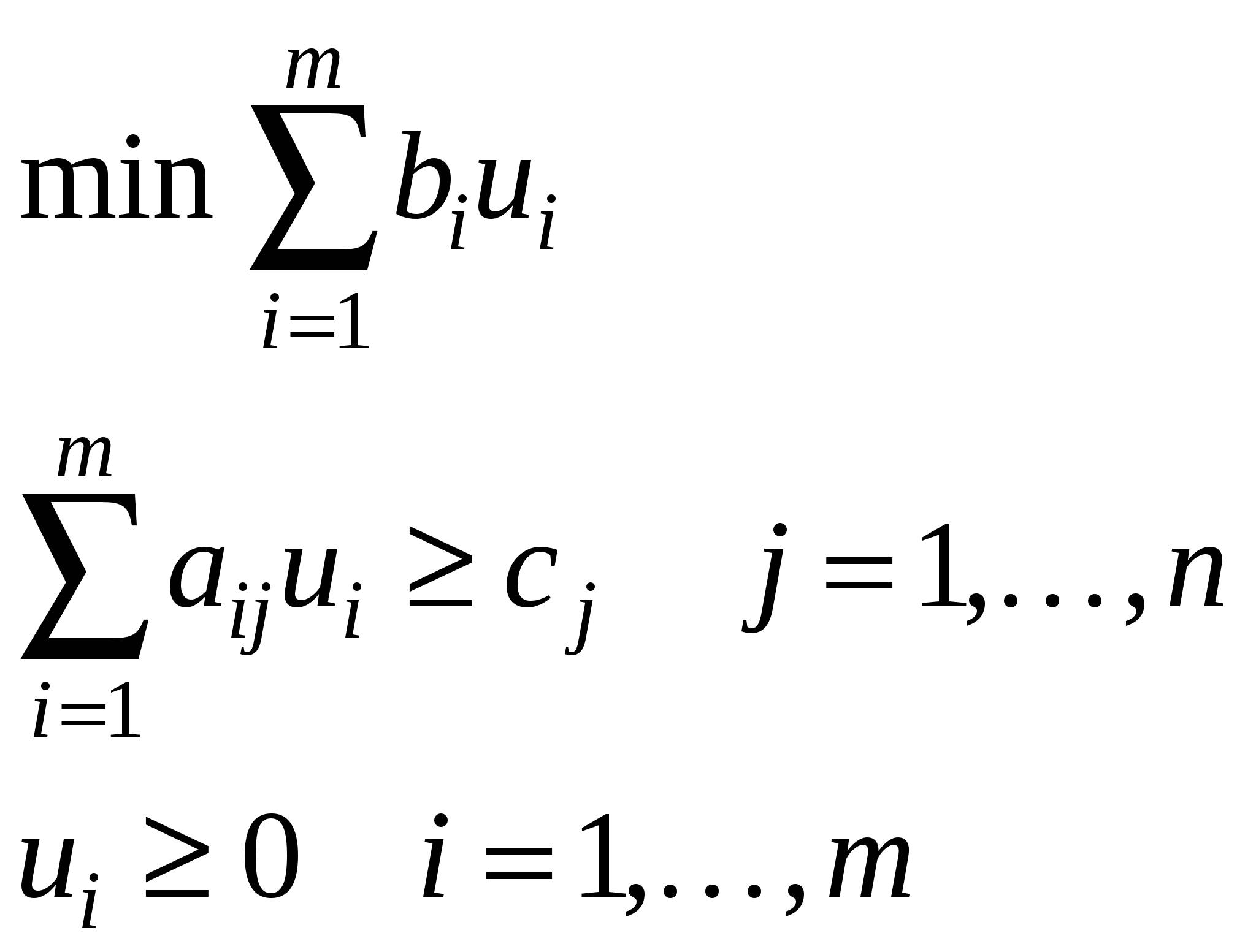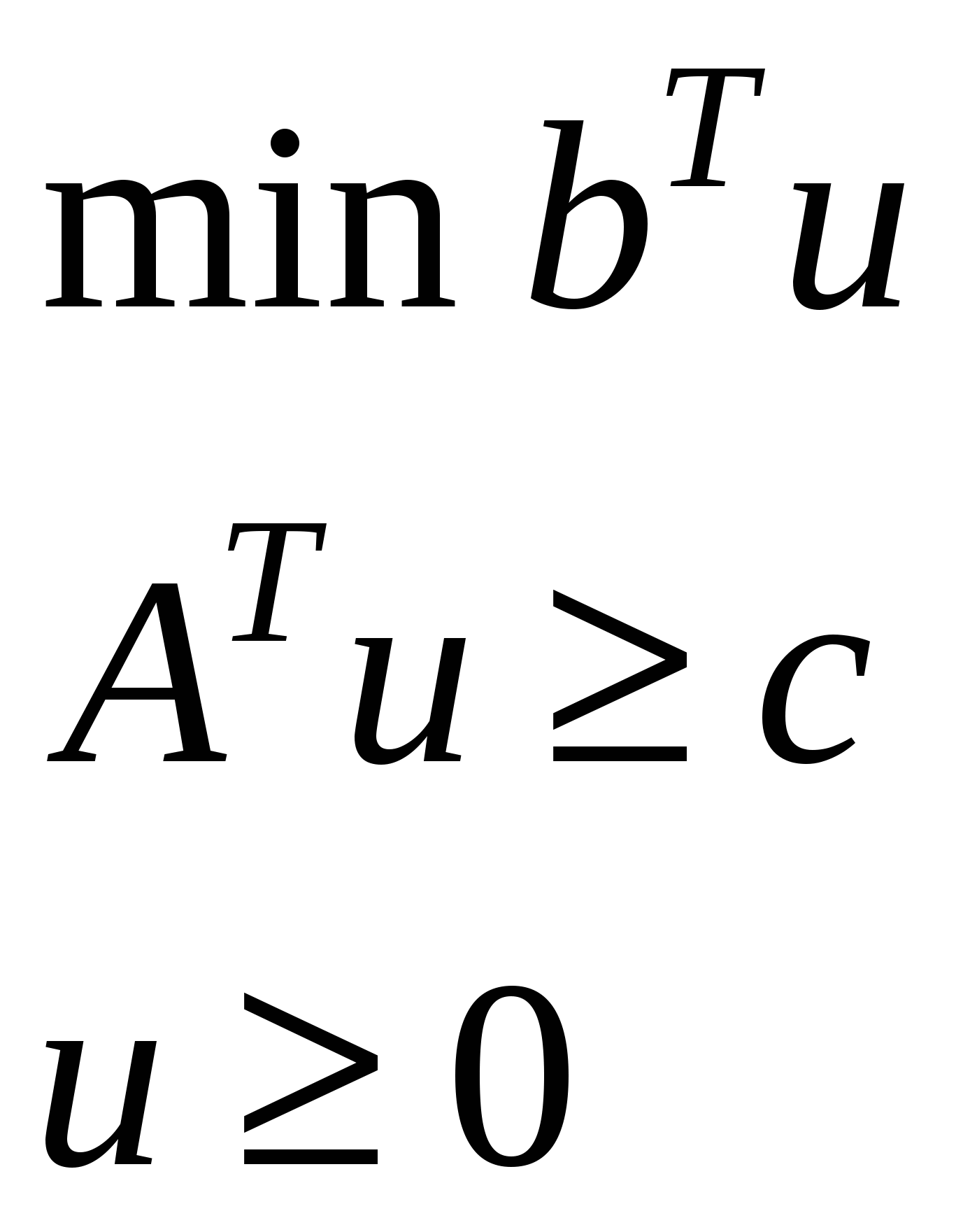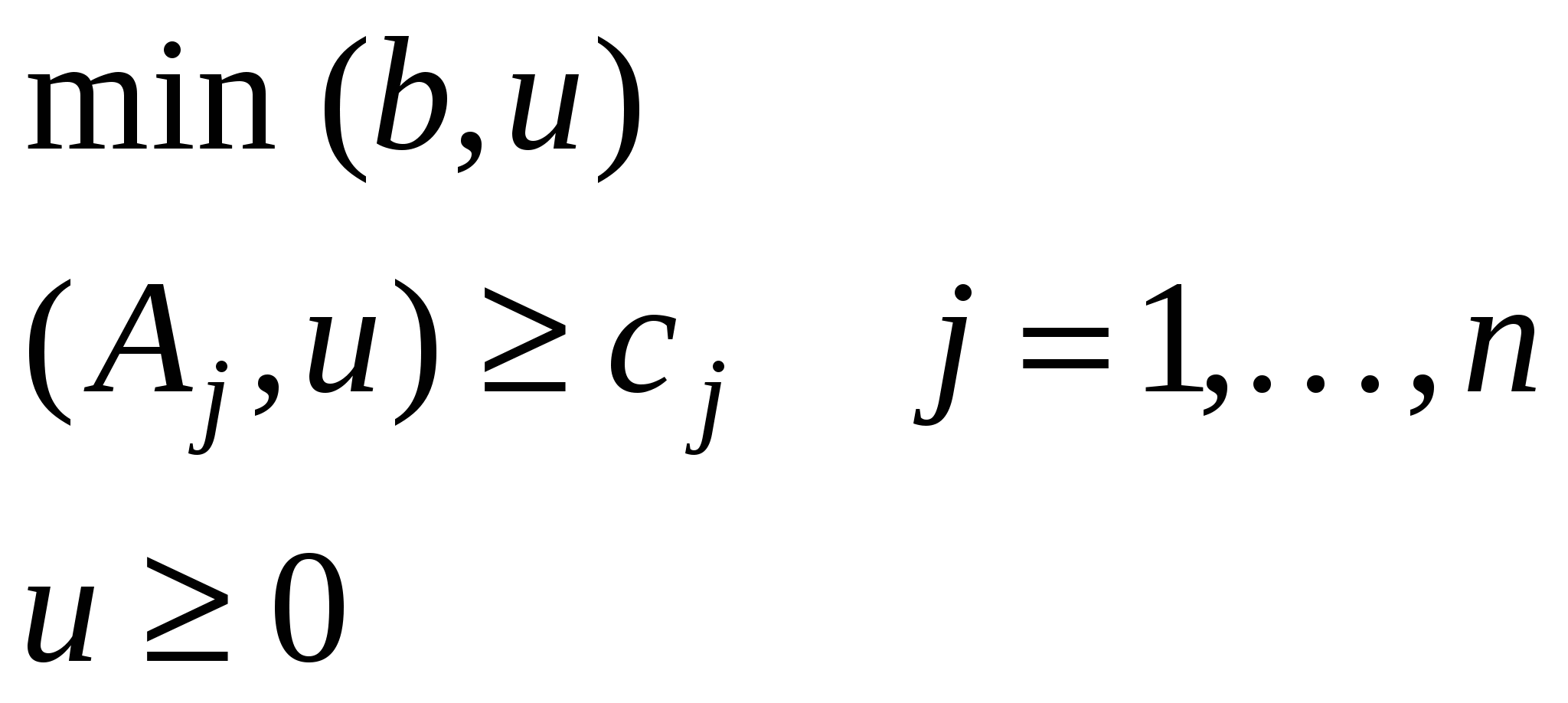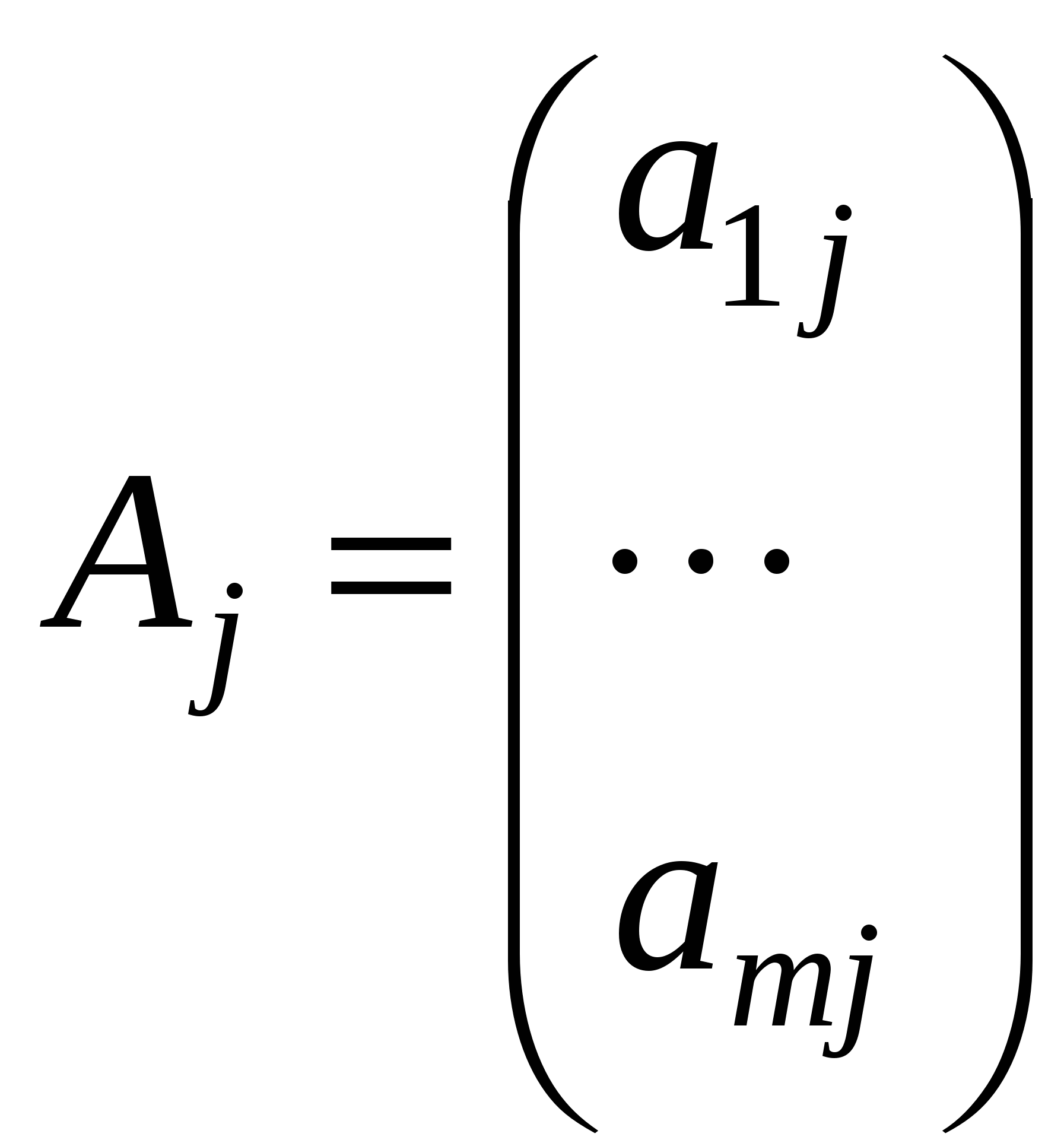Двойственная задача возникает как задача минимизации потерь ценности в производстве, при условии, что само производство функционирует оптимальным образом, то есть в соответствии с оптимальным планом задачи L.

13. 
    Правила построения двойственных моделей.
    

	L		L*
1.	Задача на max		Задача на min
2.	Матрица условий A		Матрица условий AT
3.	m ограничений n переменных		n ограничений m переменных
4.	с – вектор цели b – вектор ограничений		b – вектор цели c – вектор ограничений
5.	Ограничение ≤		Ограничение ≥
6.	x ≥ 0		y ≥ 0

Двойственная у двойственной

L*:
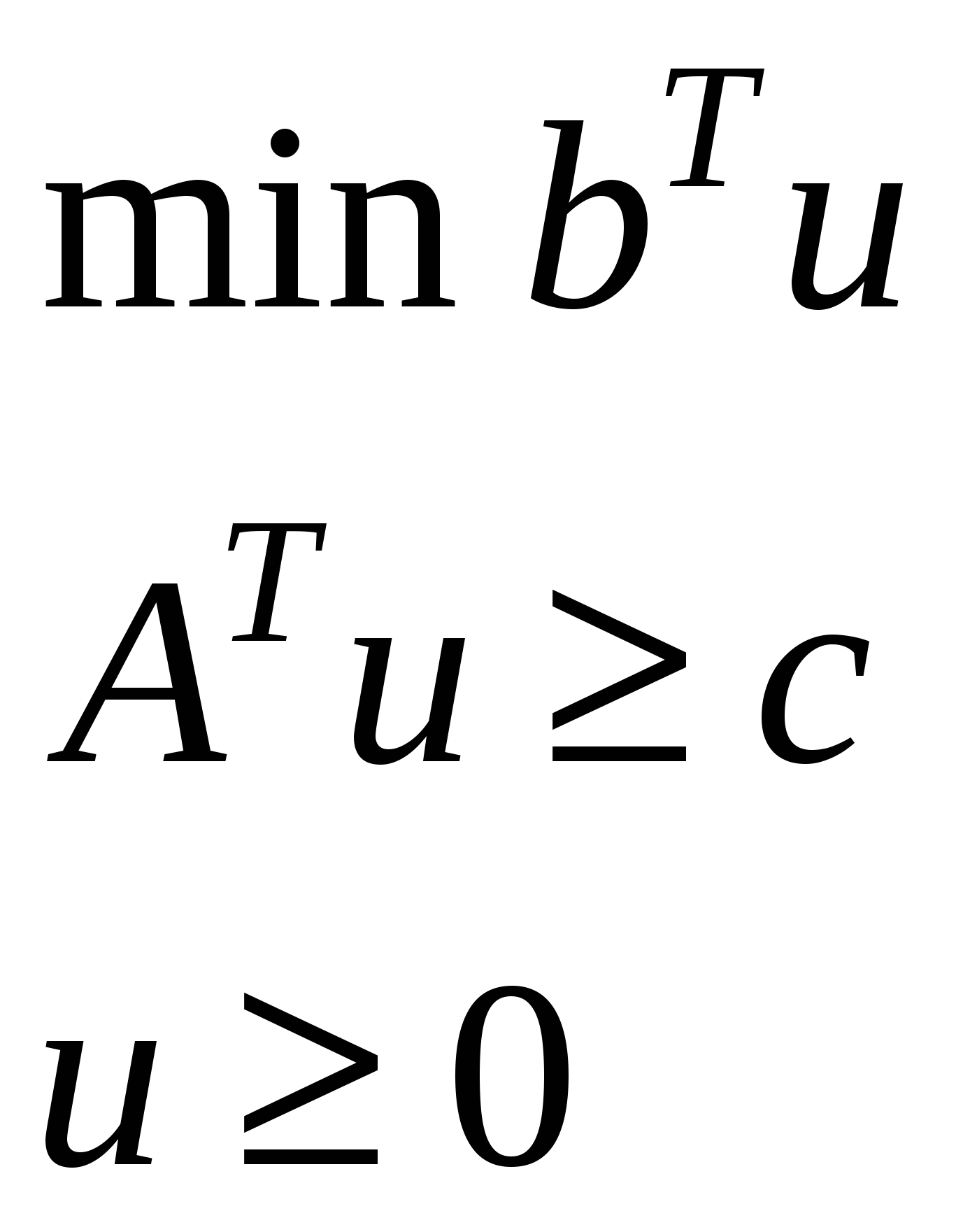
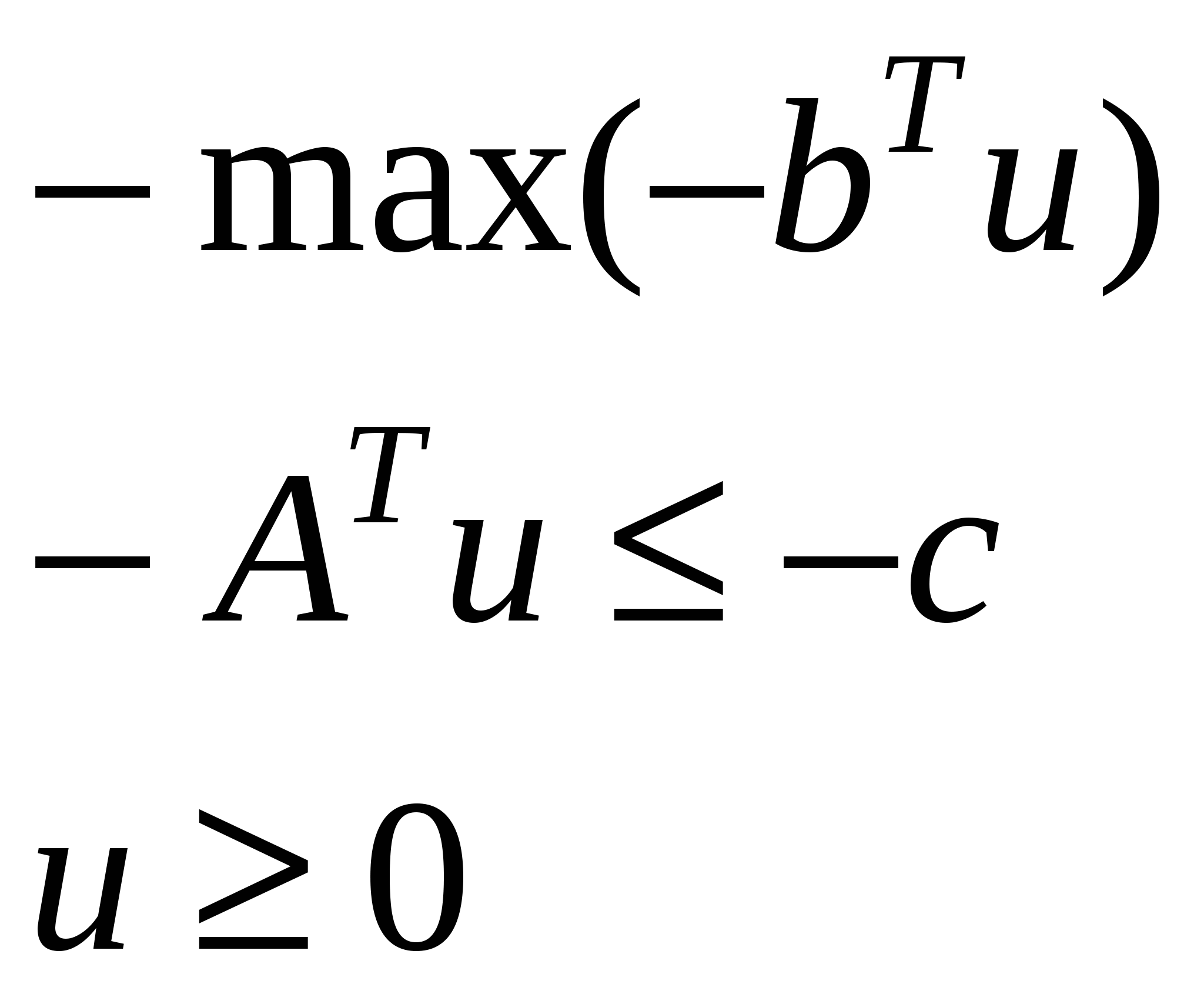
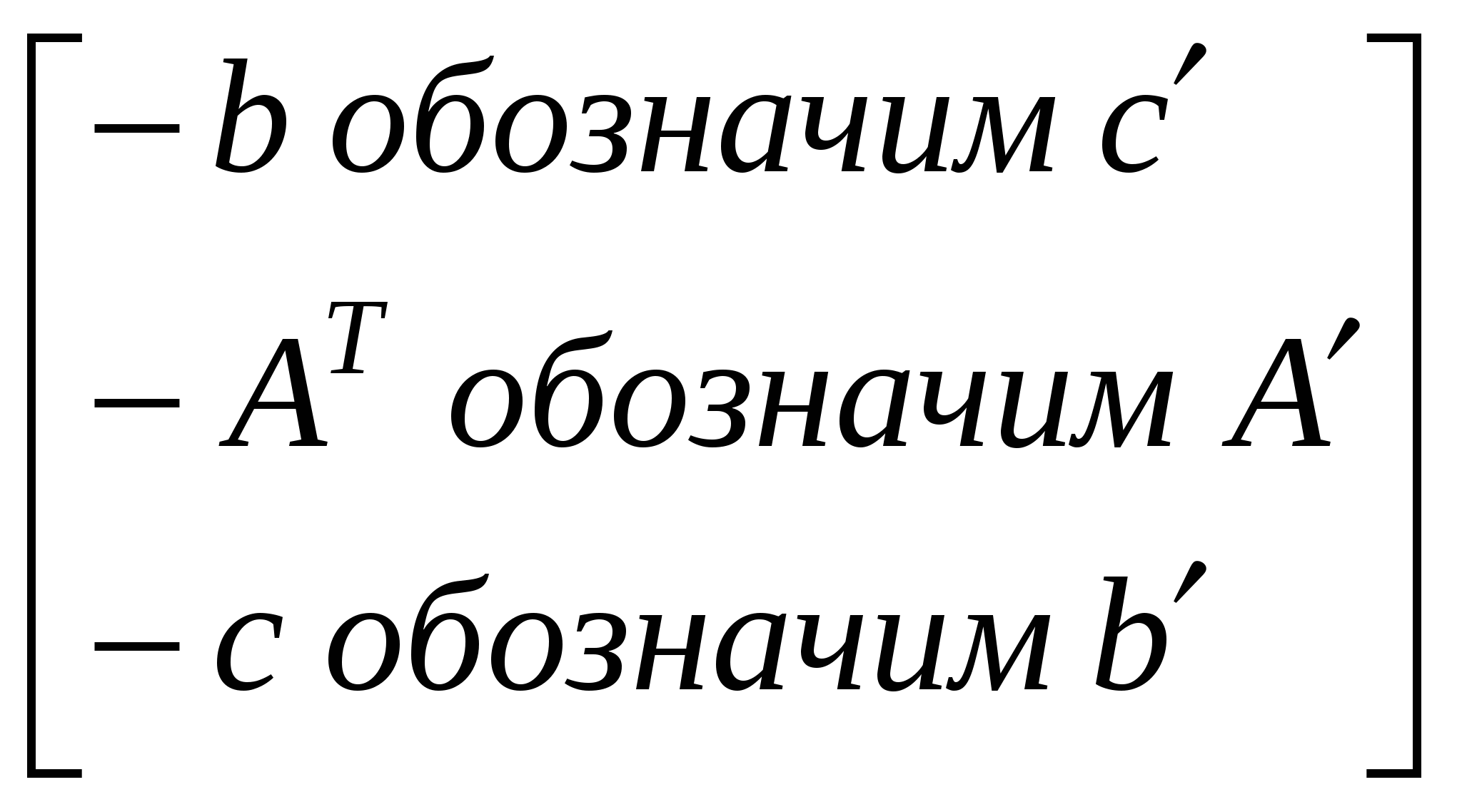
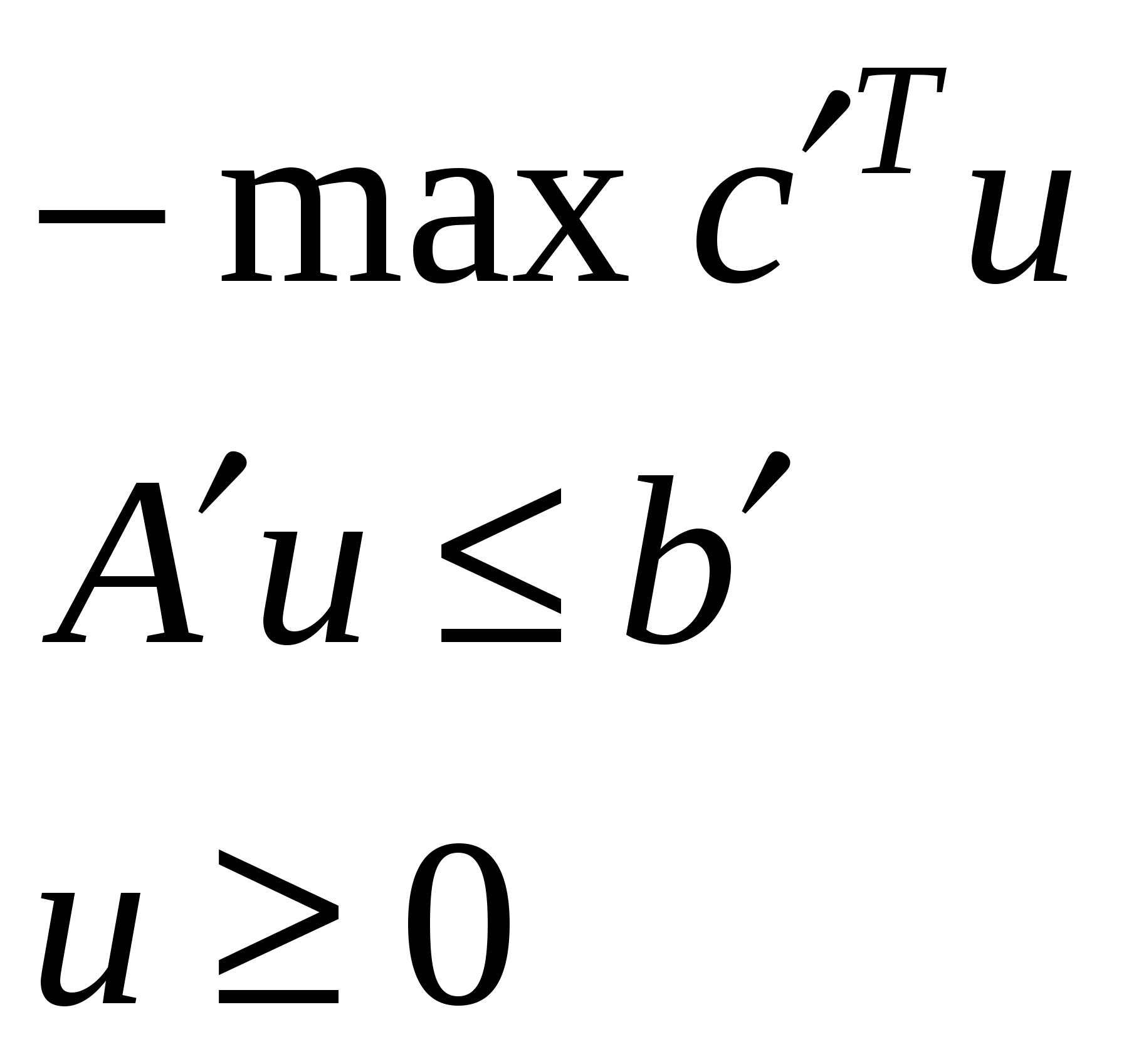
Переходим к двойственной


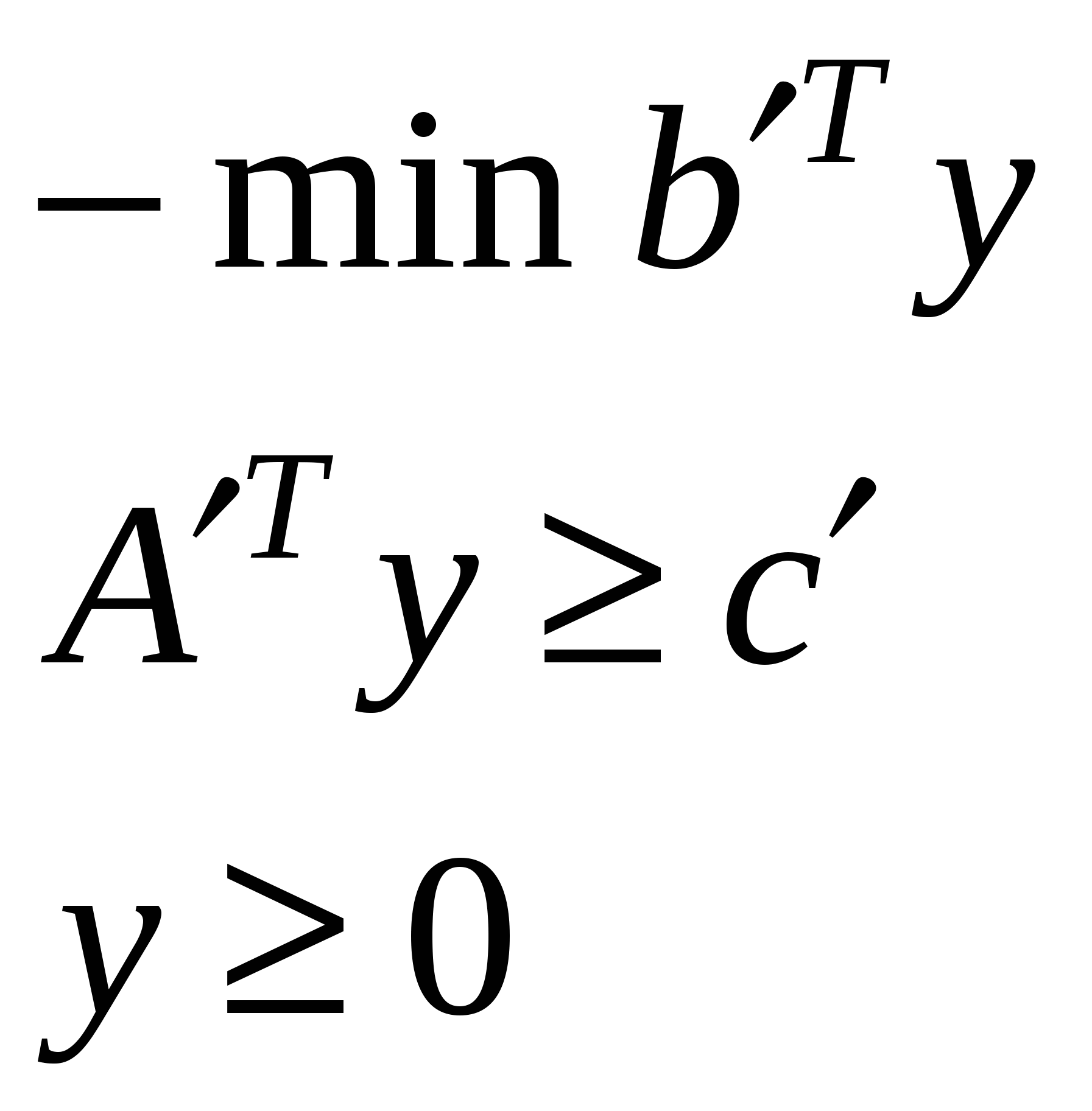
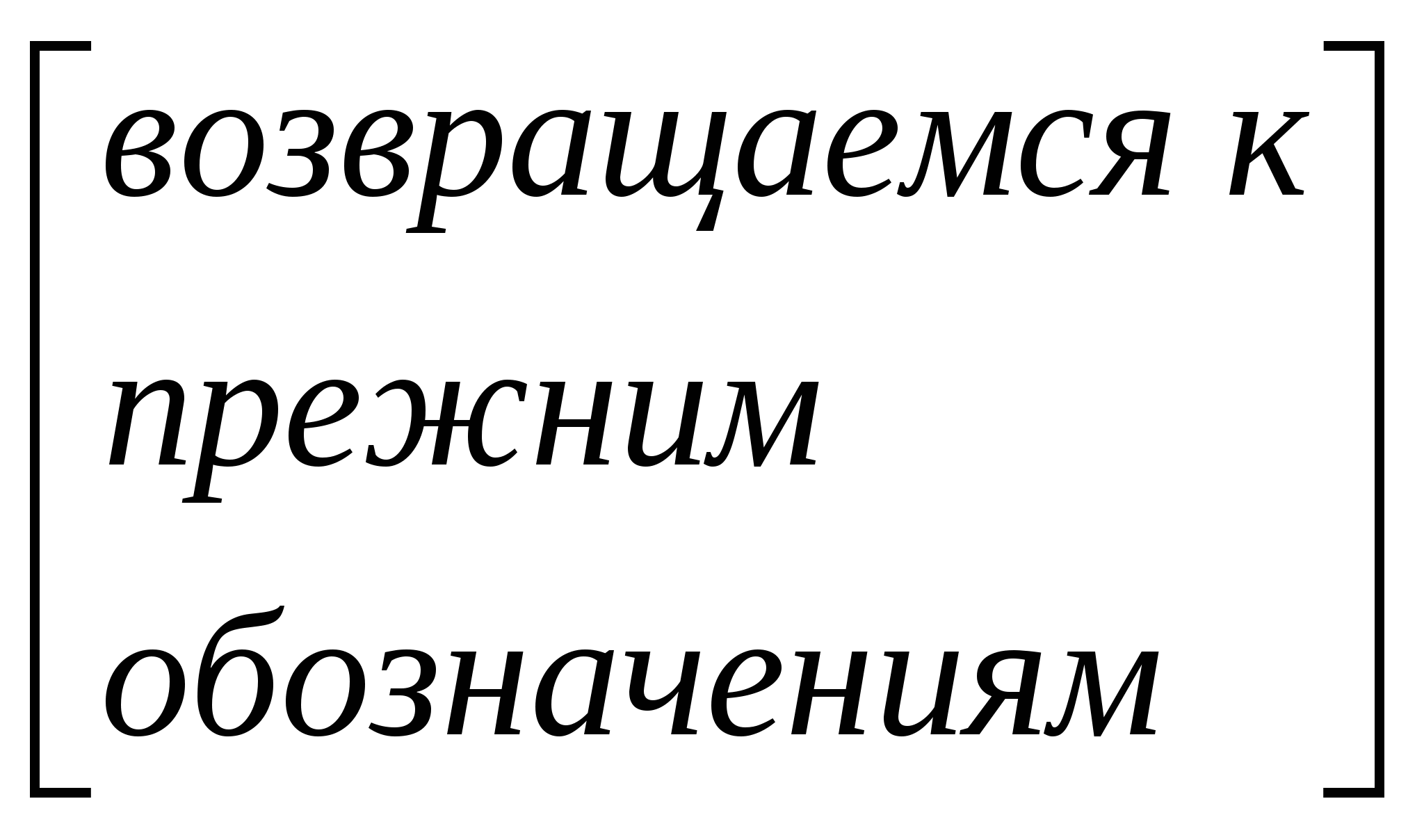
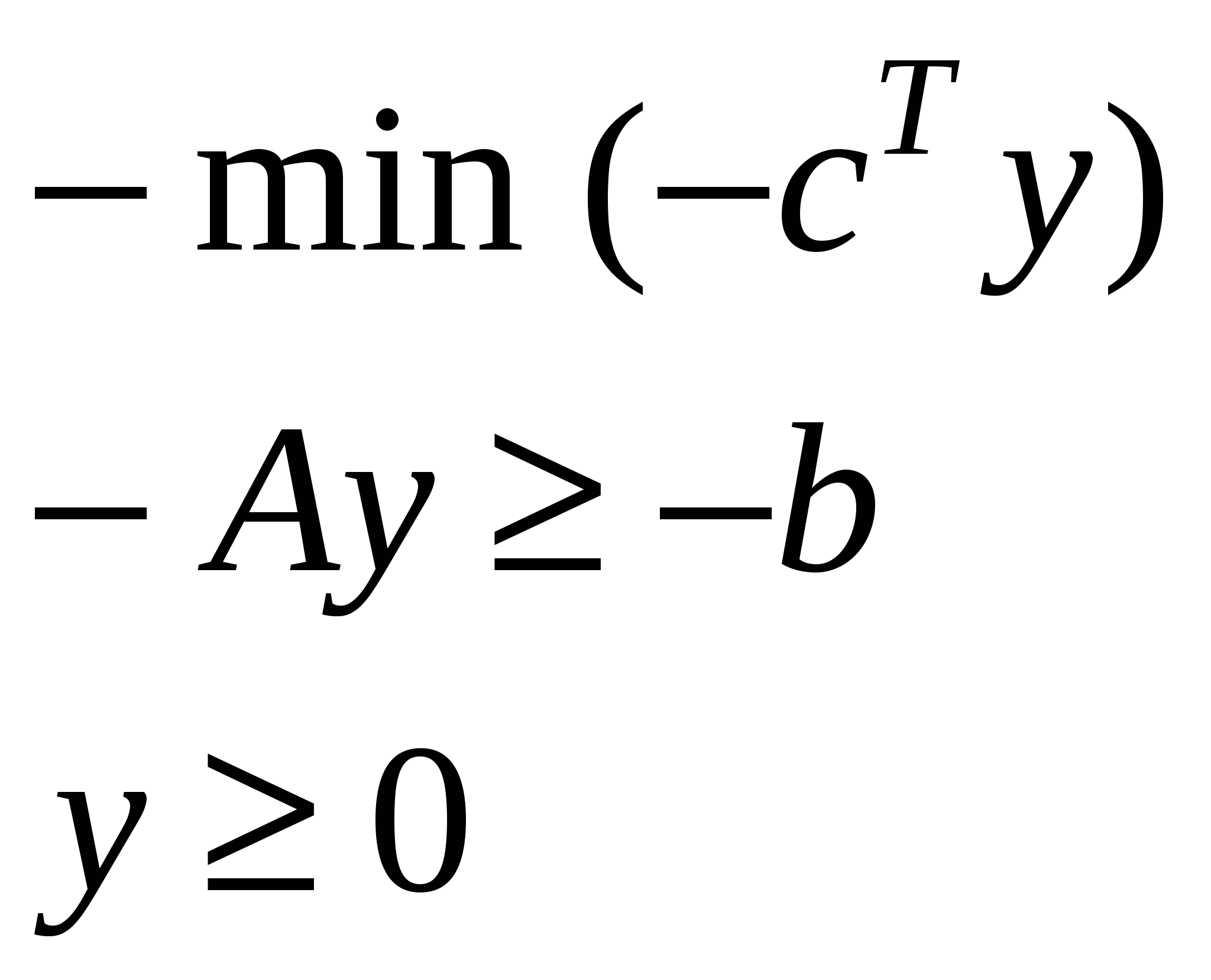
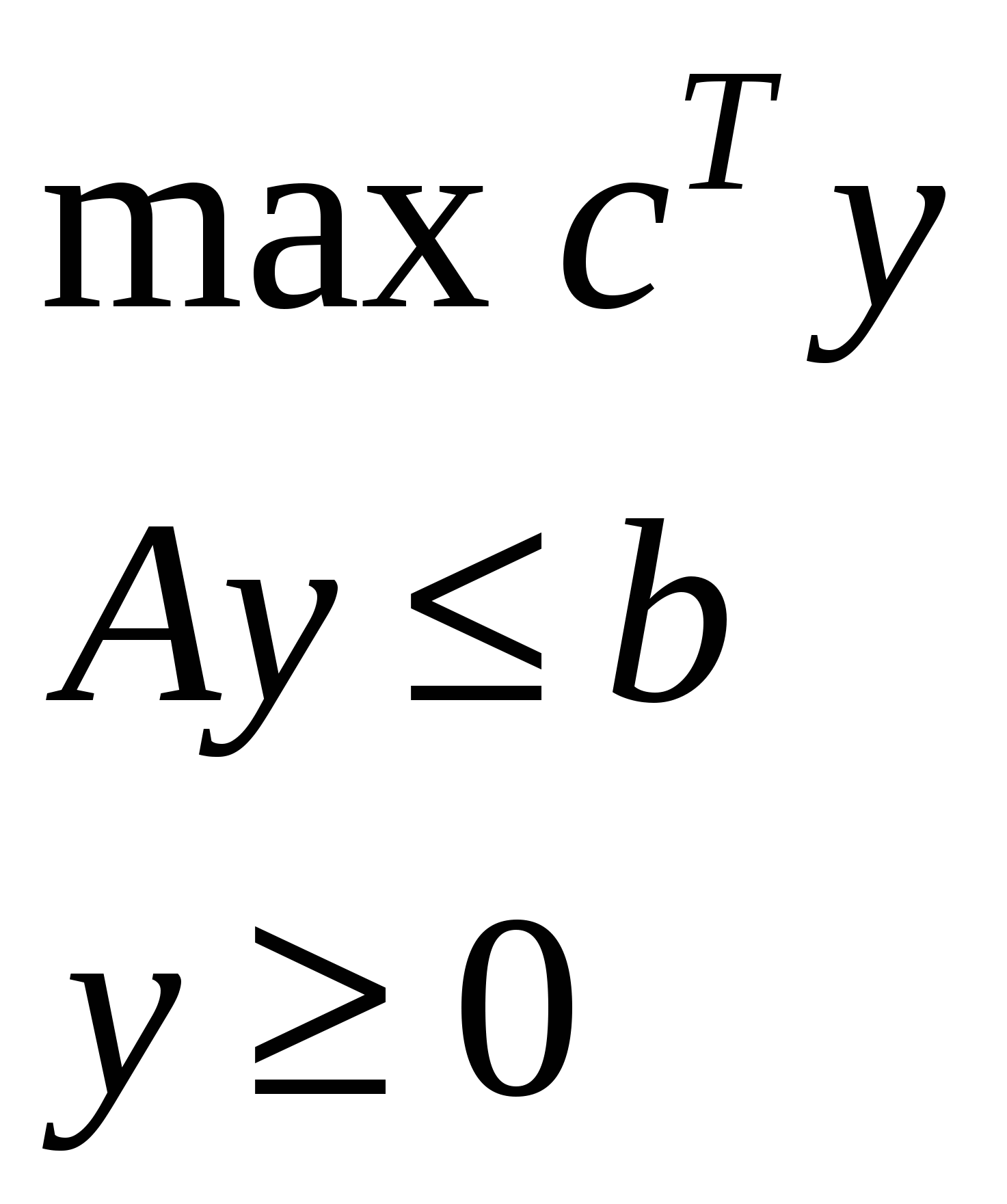
Теорема: двойственная задача для двойственной совпадает с исходной.
Прямые и двойственные задачи

	Прямая		Двойственная
1.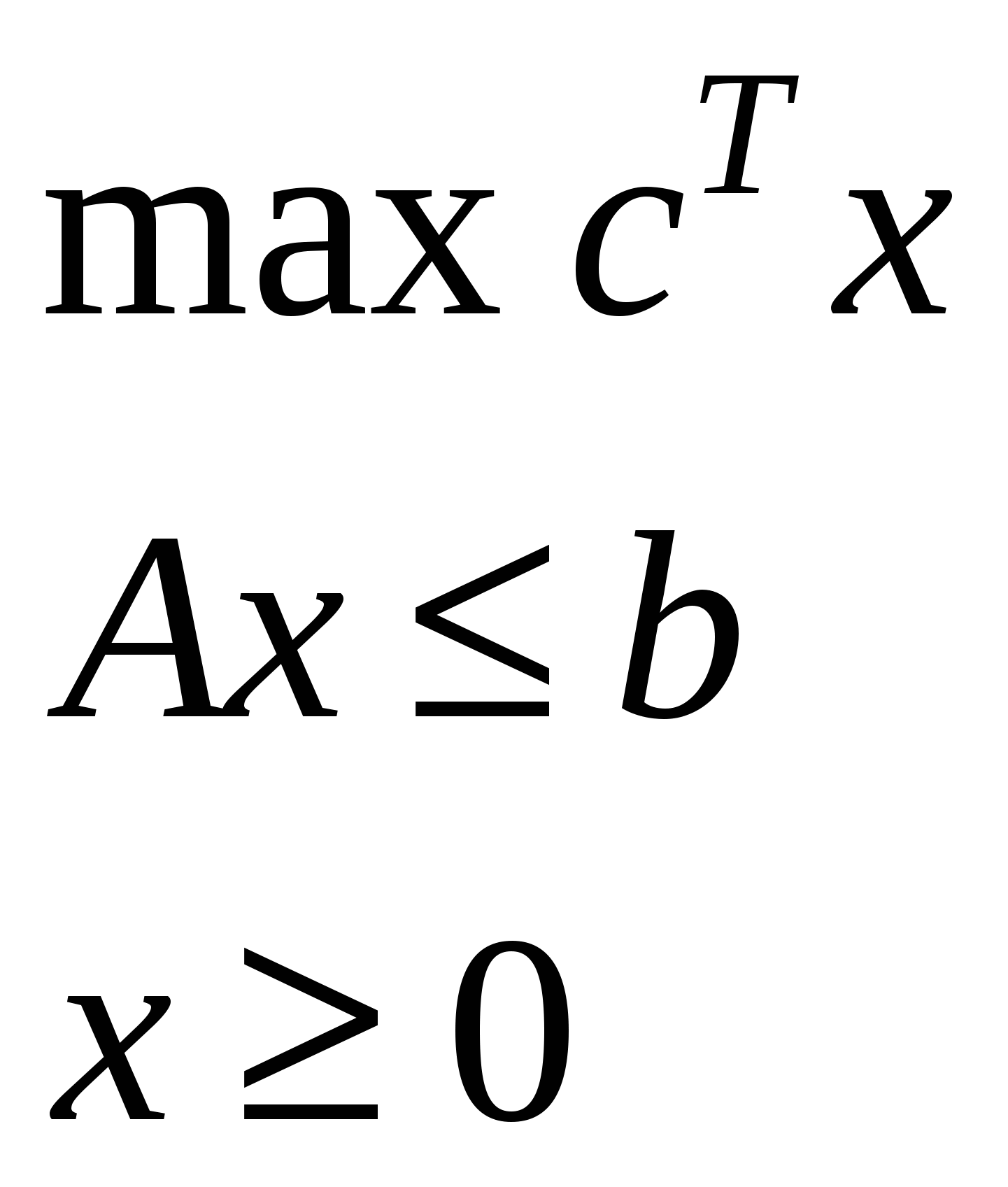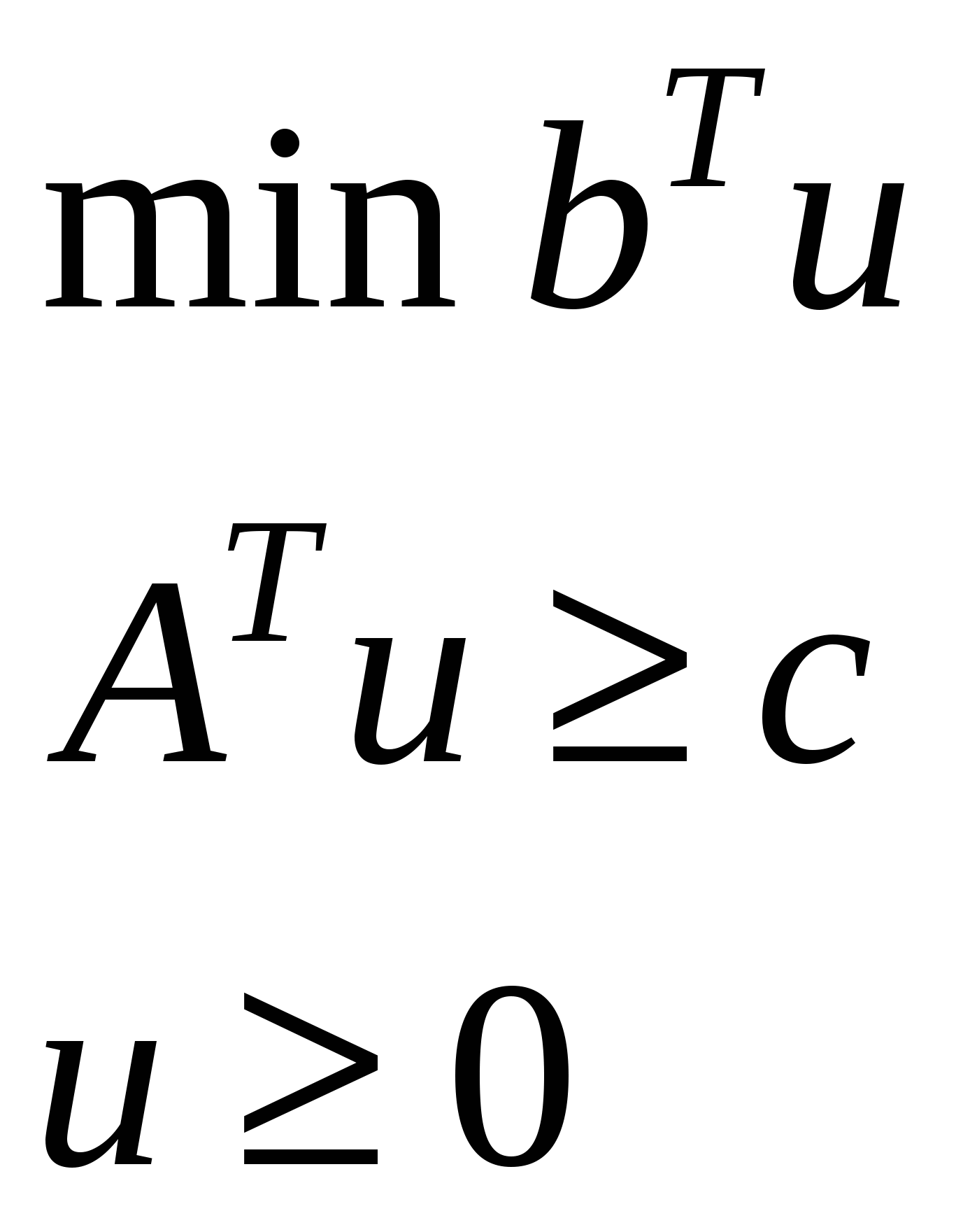
2.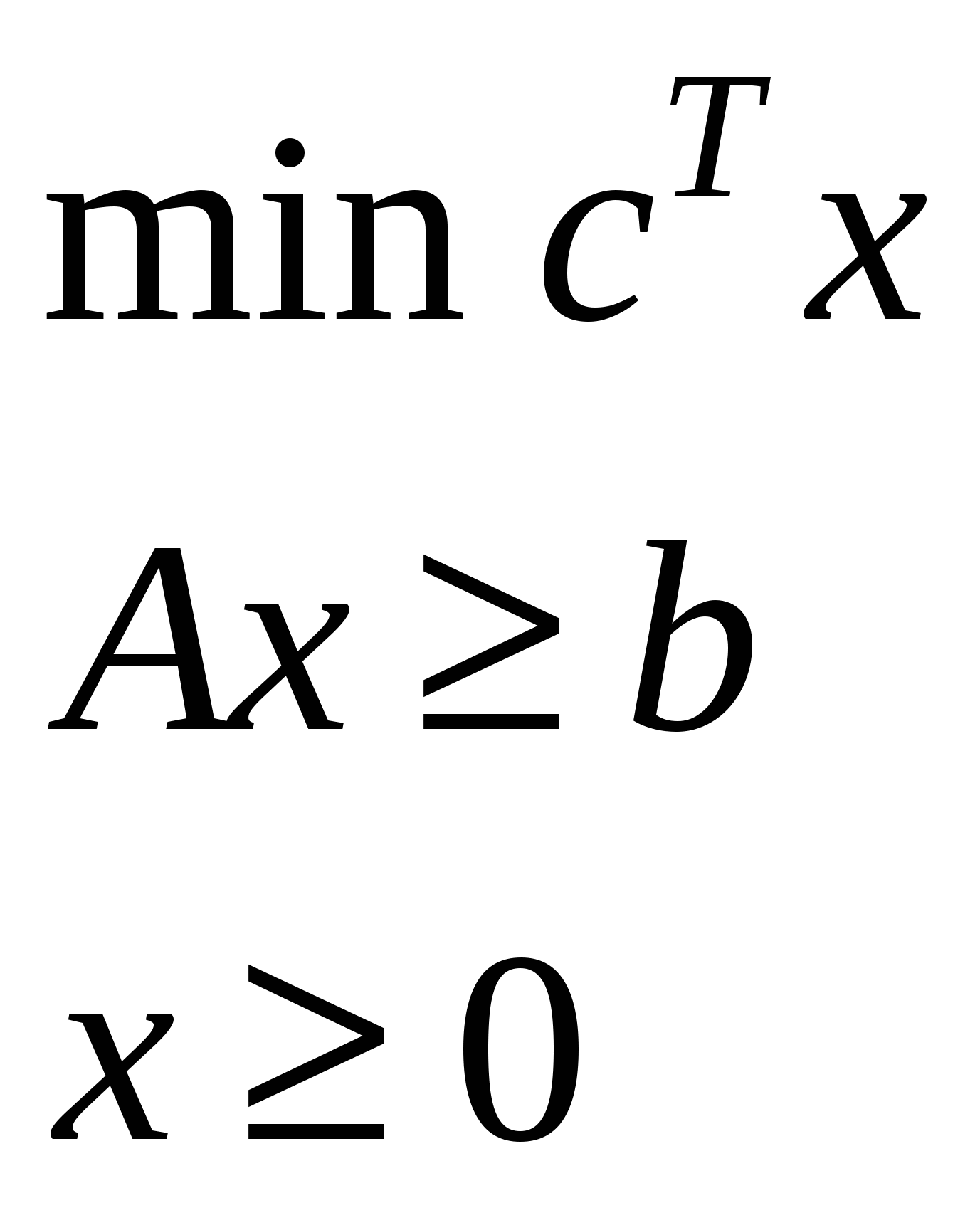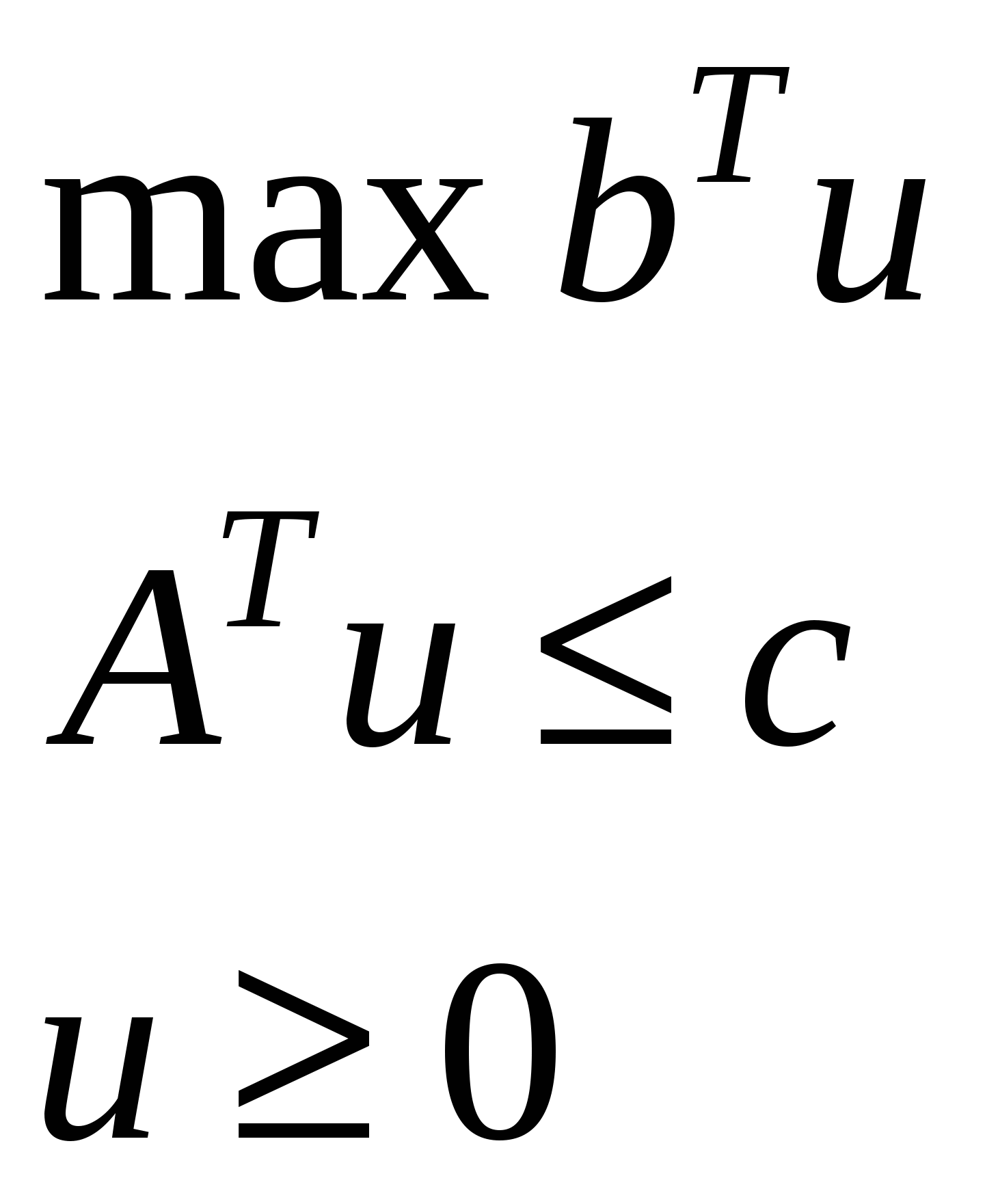
3.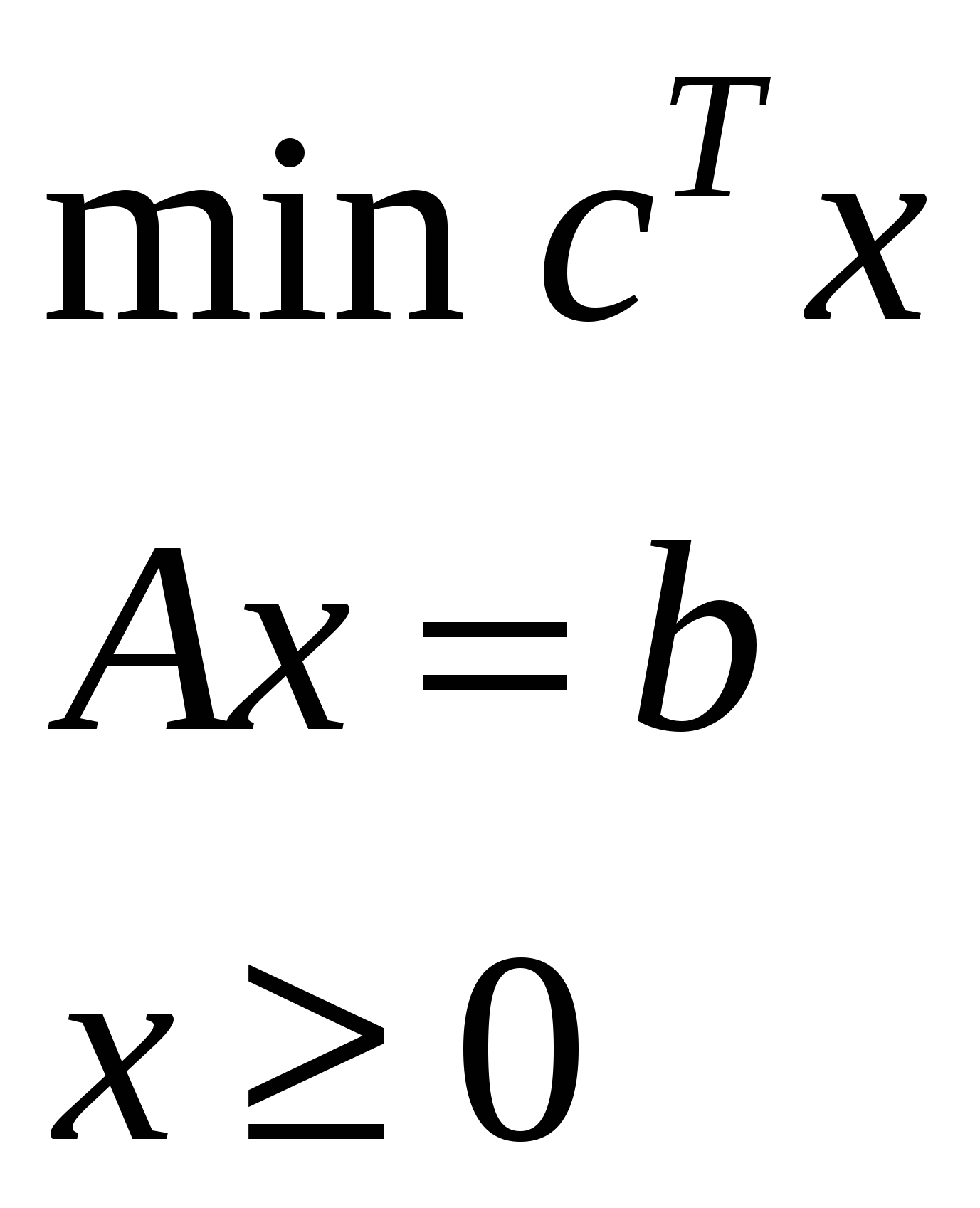
4.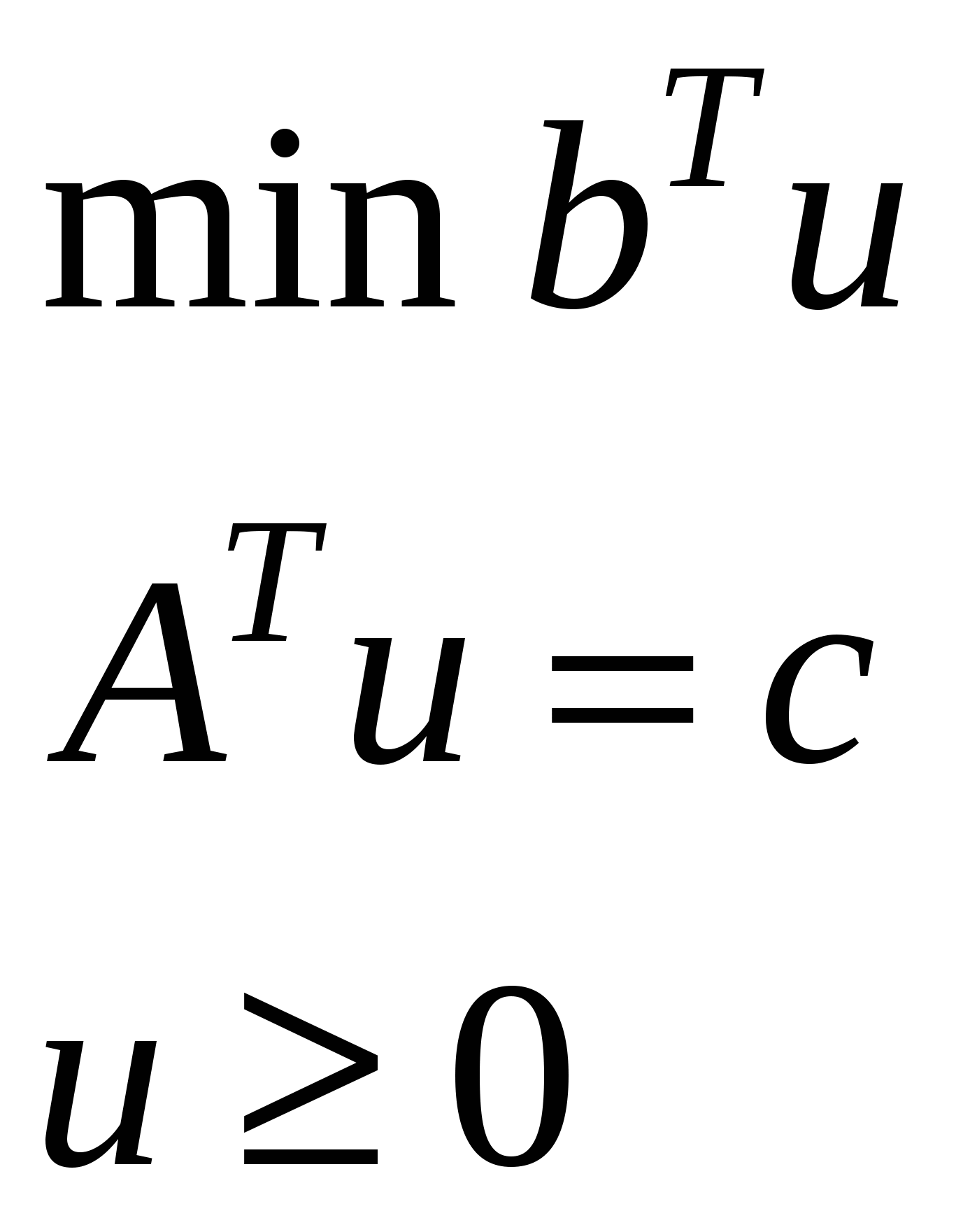

Для 3 и 4 если в исходной ограничения =, то в двойственной переменные свободные и наоборот, если в исходной переменные свободные, то в двойственной ограничения =.
Как получили 3:

14. 
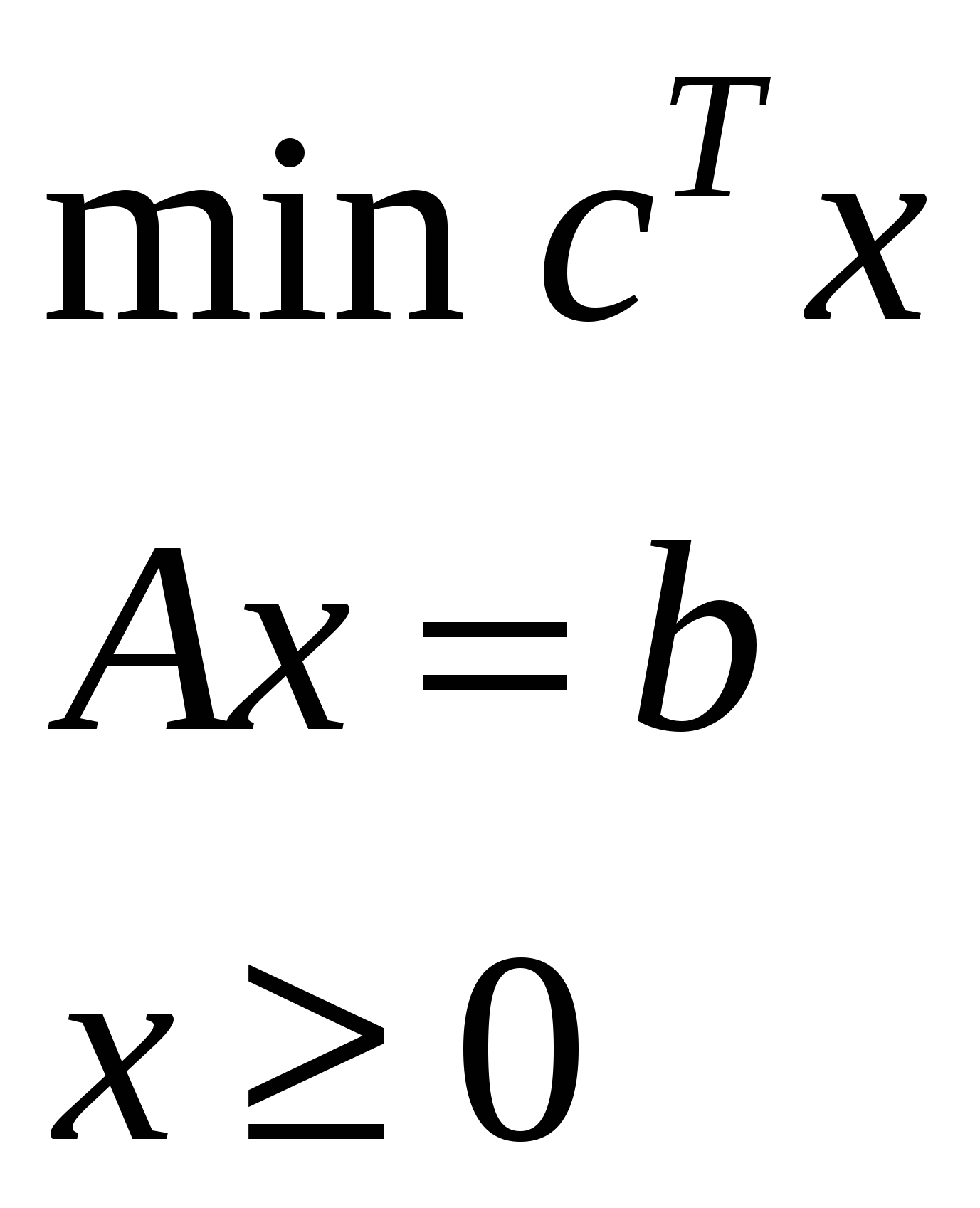
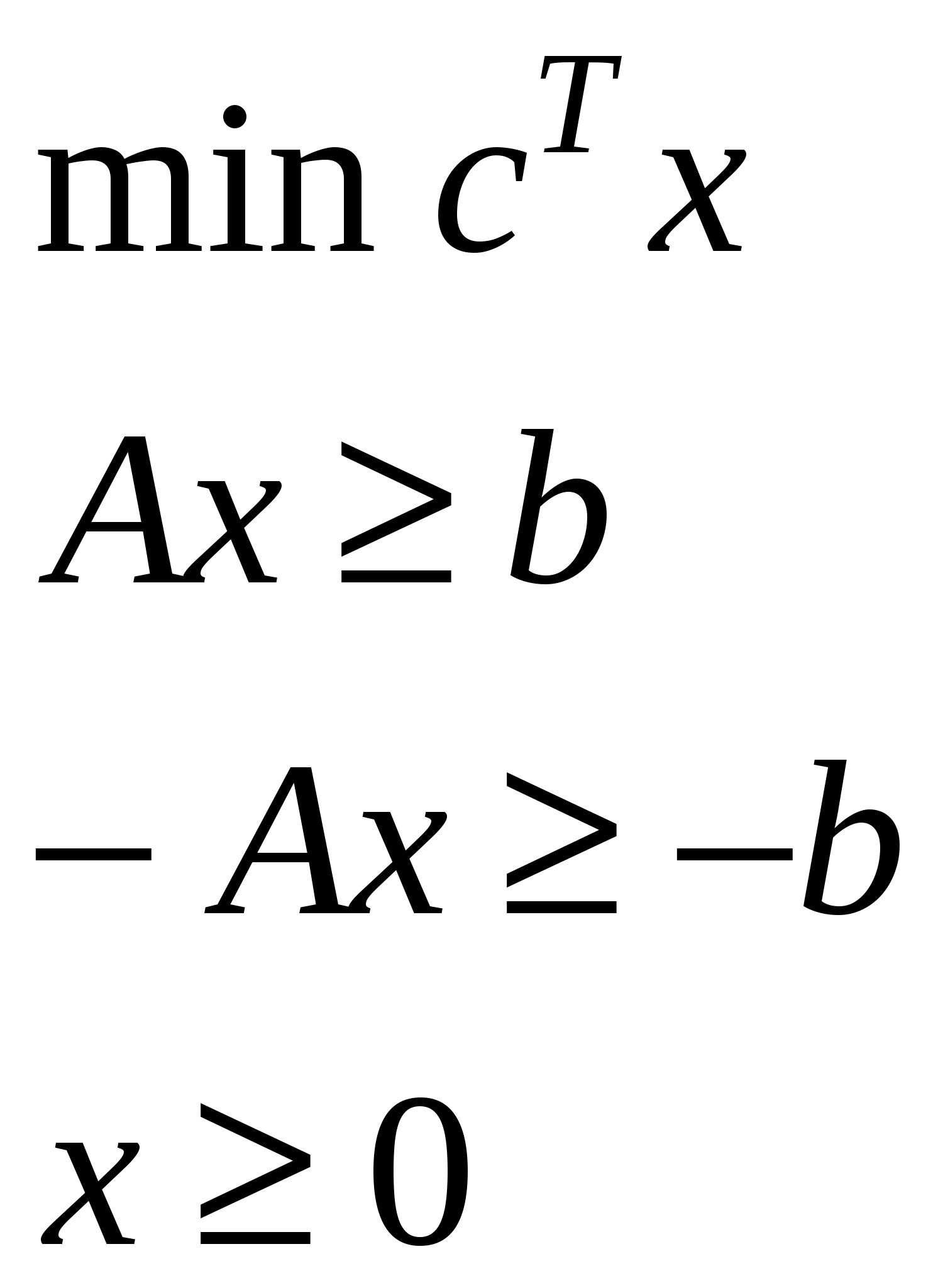
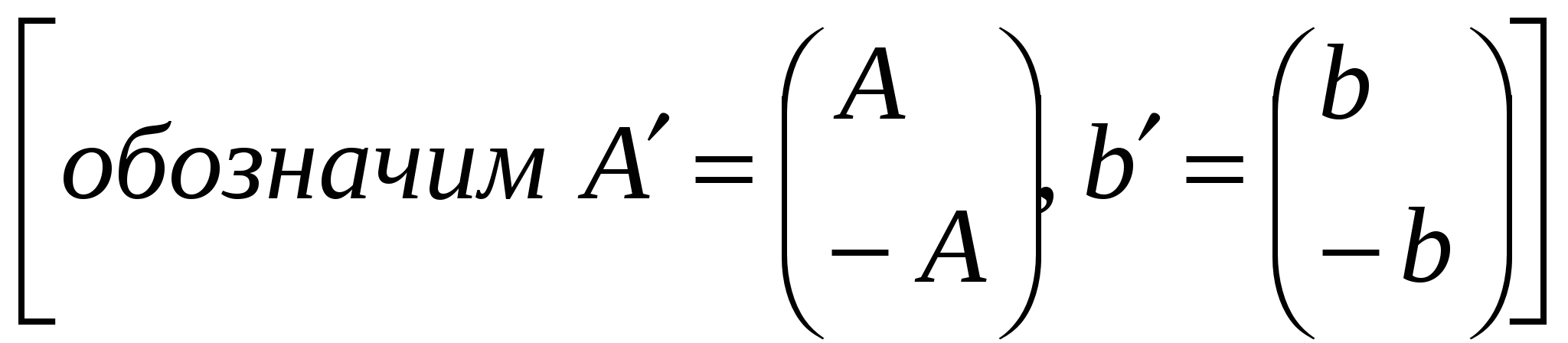
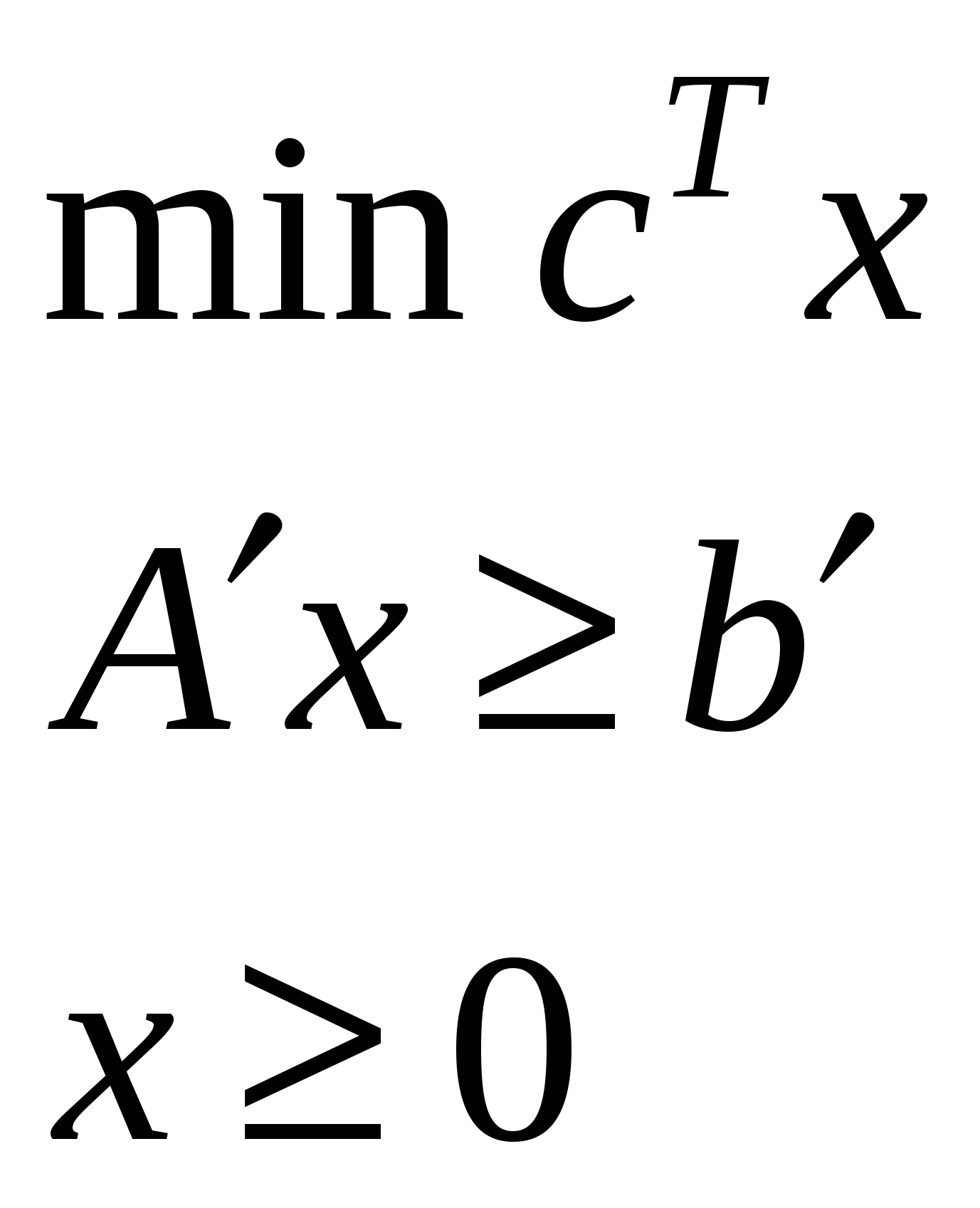
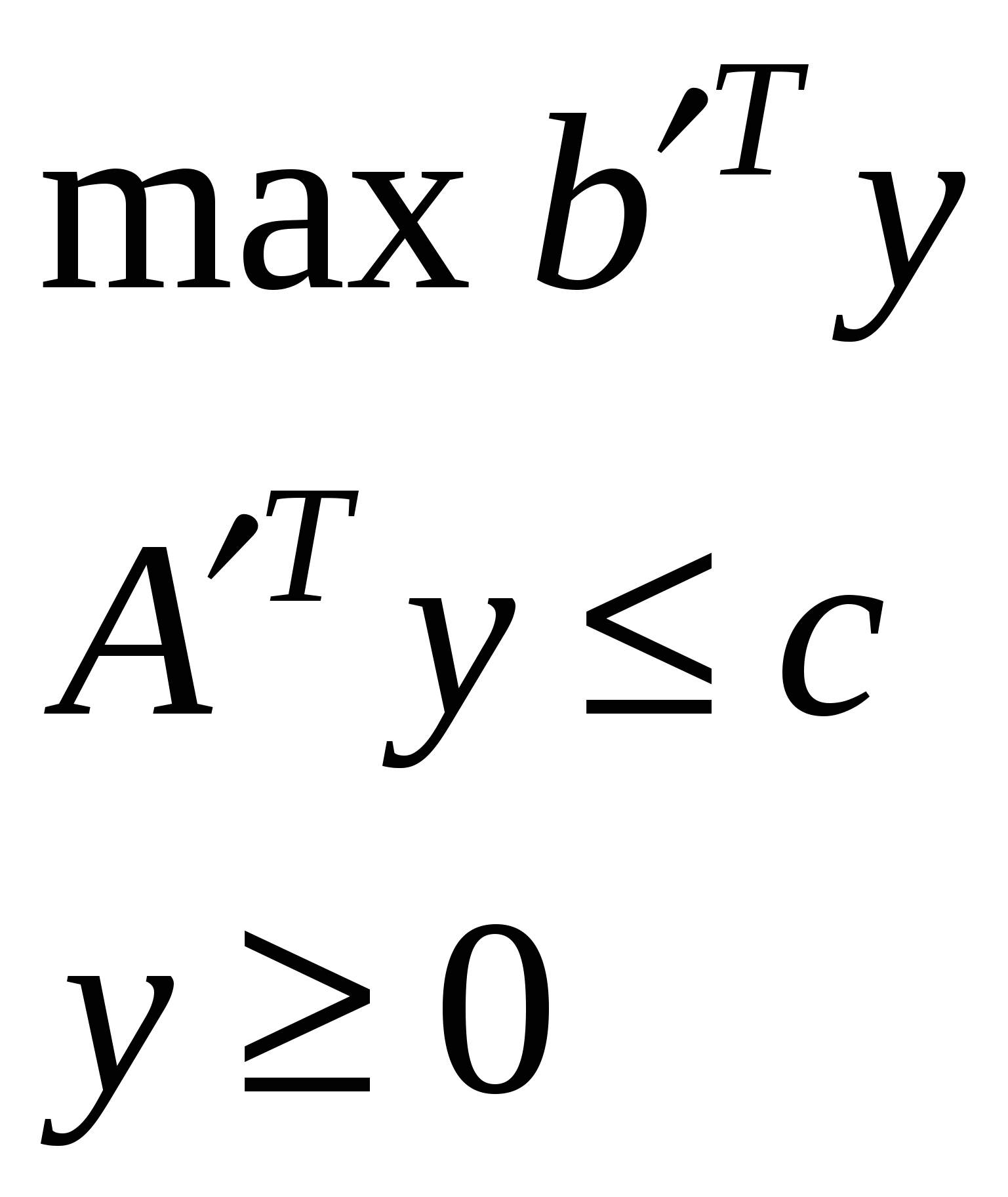
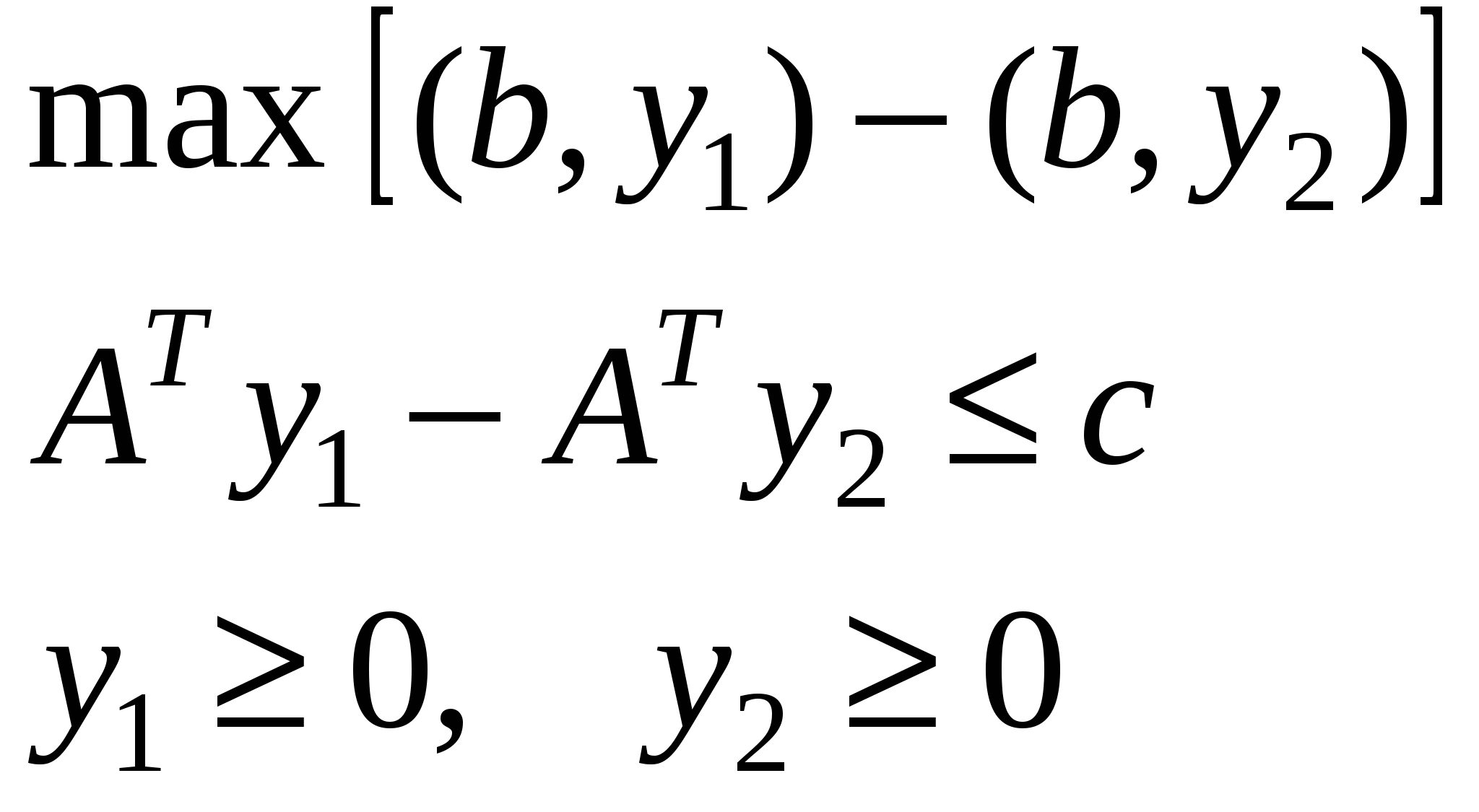
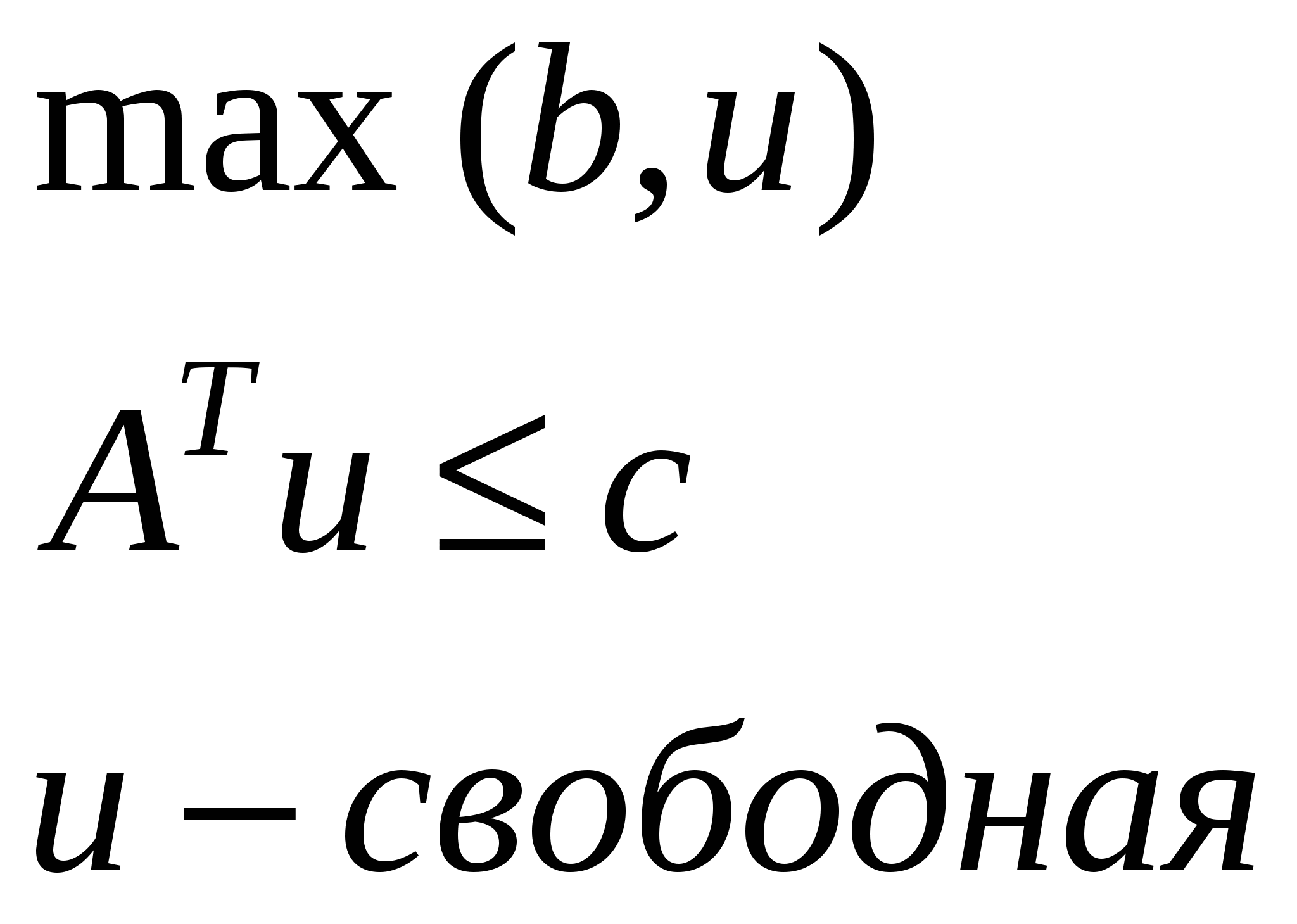
    Теоремы двойственности в ЛП.
    

Слабая теорема двойственности

–целевая функция двойственной задачи ≥ целевой функции исходной задачи.

Следствия:

1. 
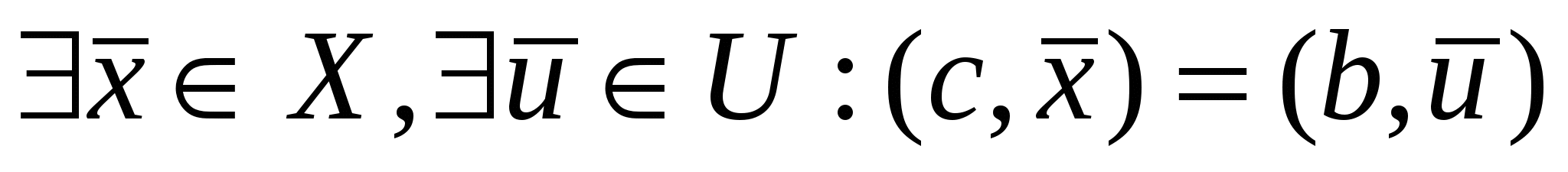   Если , то 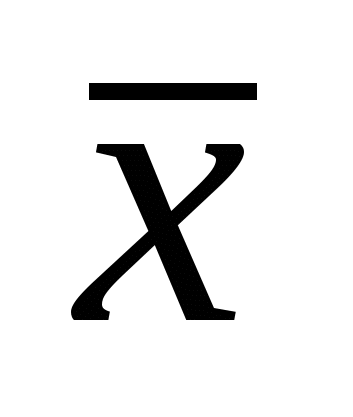– решение исходной (L), 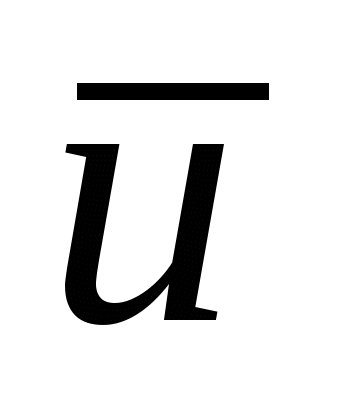– решение двойственной (L*)
   
2. 
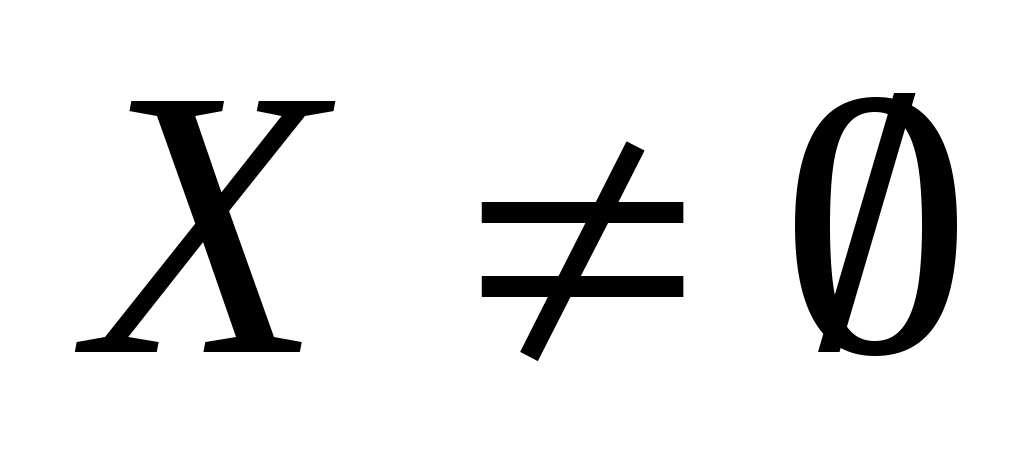   Если и 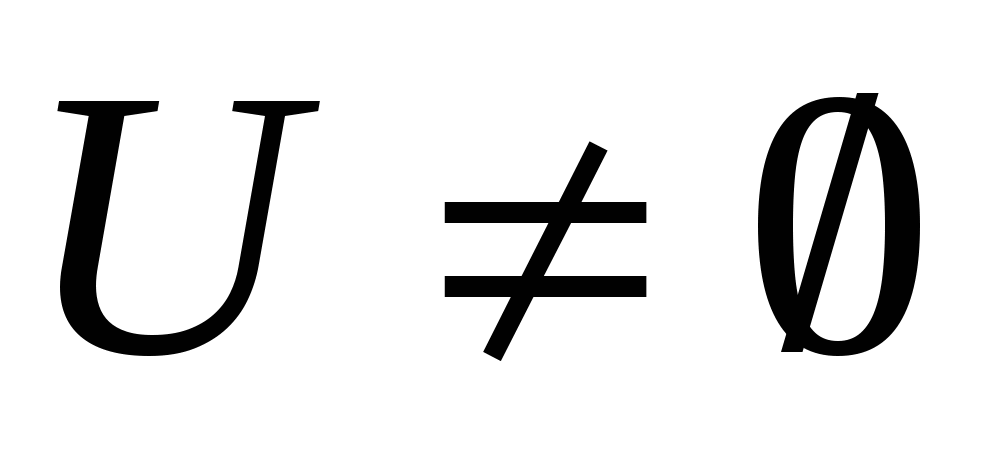, то (L) и (L*) имеют решение
   
3. 
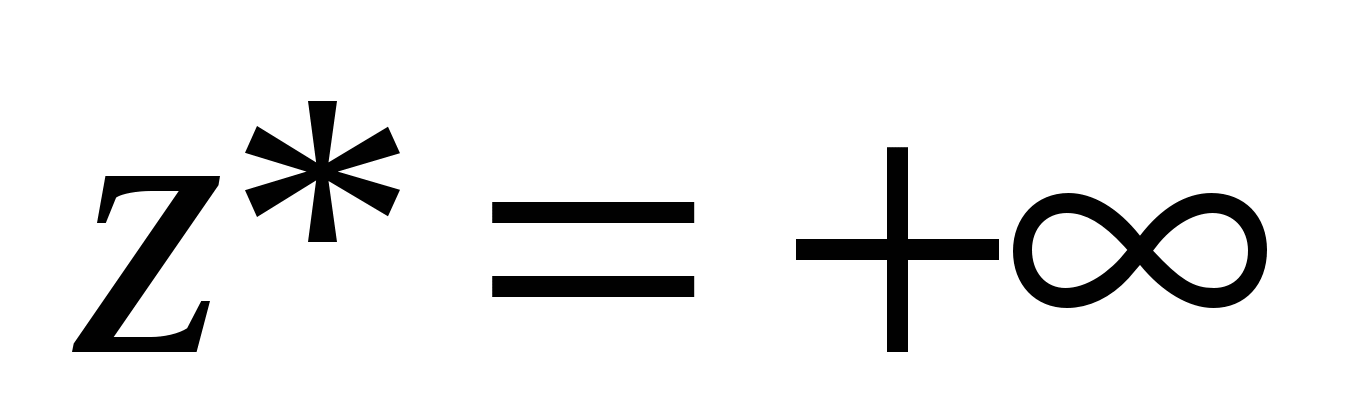   Если , то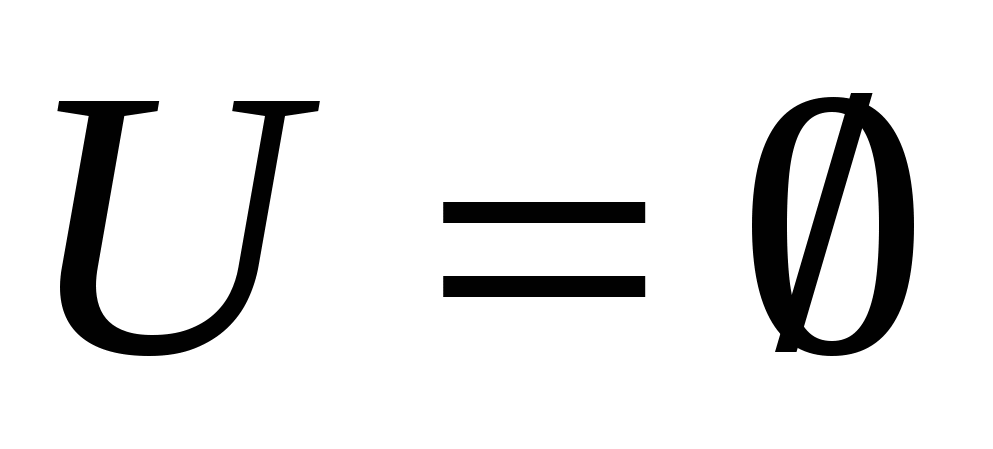
   

Если в двойственной , то
Сильная теорема двойственности

Если разрешима одна из двух задач (L) или (L*), то разрешима и другая и их оптимальные значения совпадают.

15. 
    Условия оптимальности в ЛП и их экономический смысл.
    

L – стандартная задача, L* – двойственная задача.

Вектор оптимален в (L) 

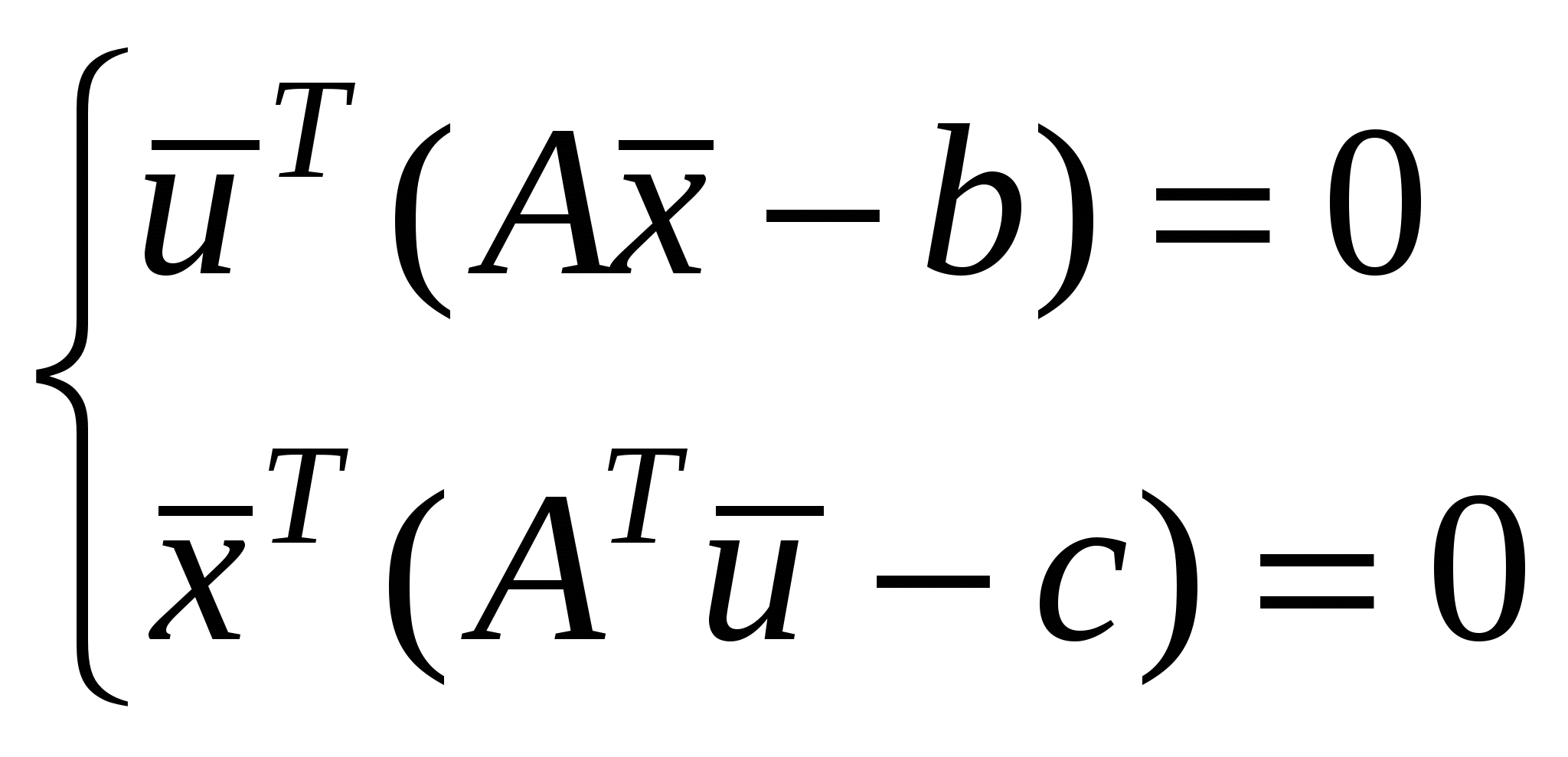– условие оптимальности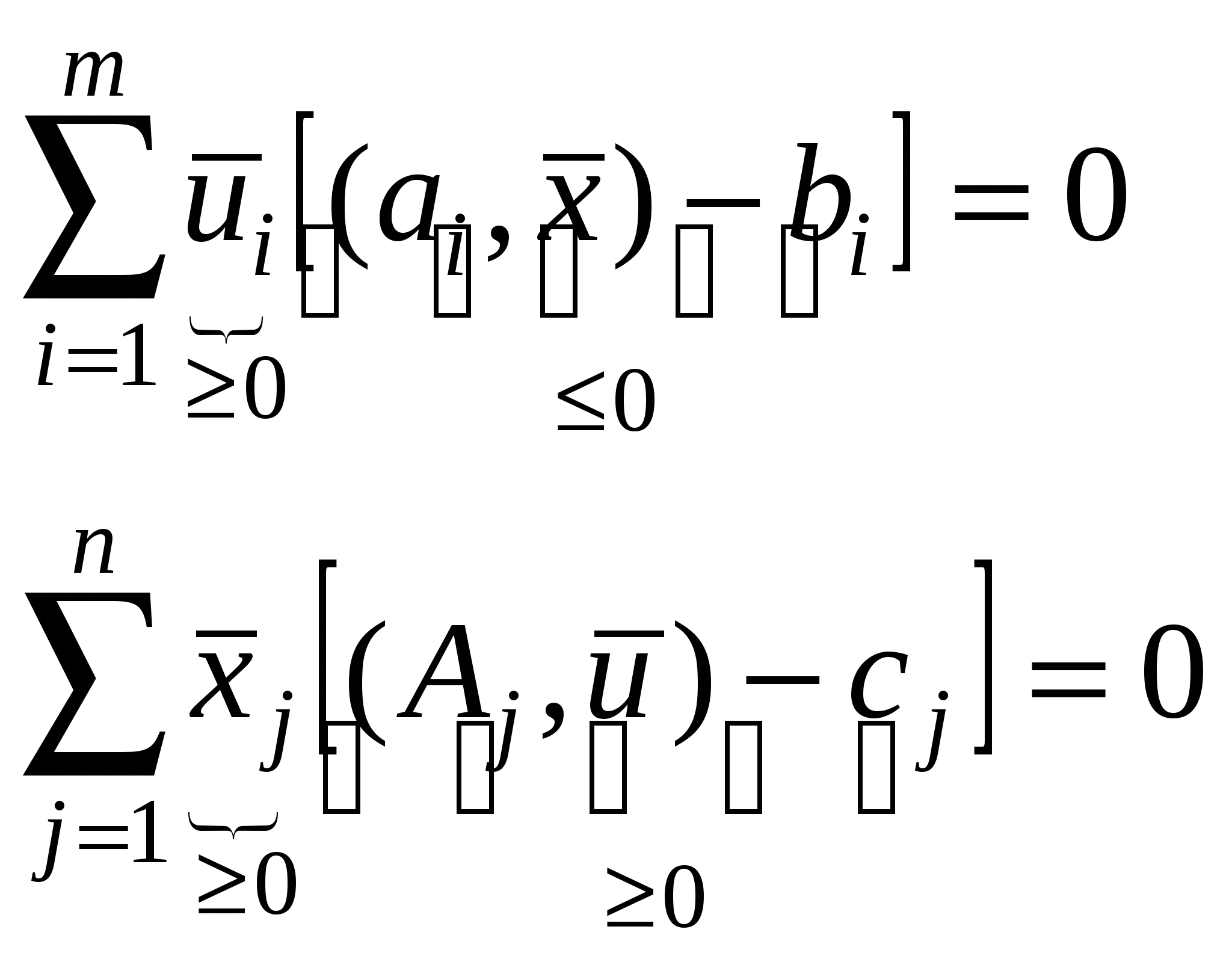



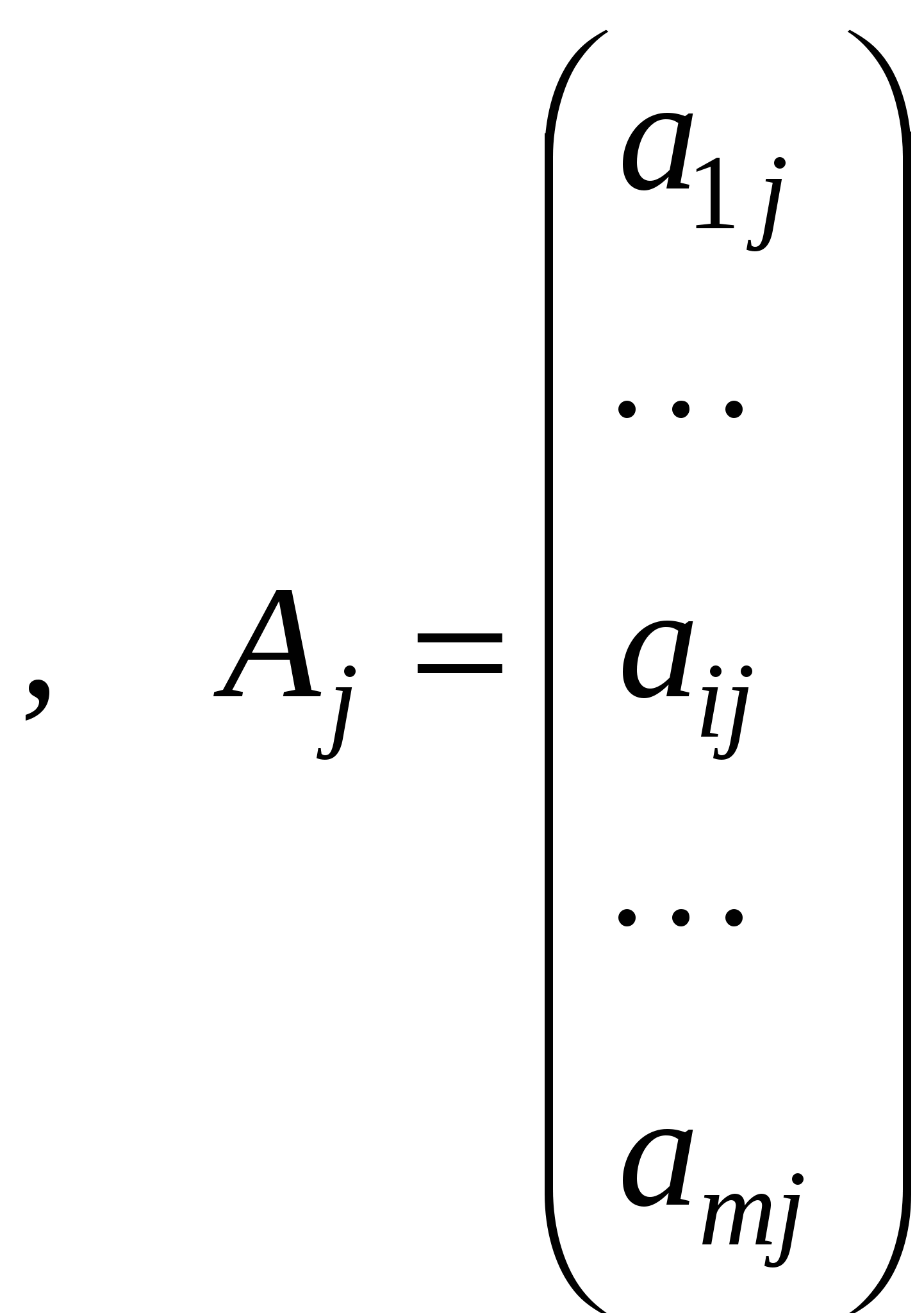
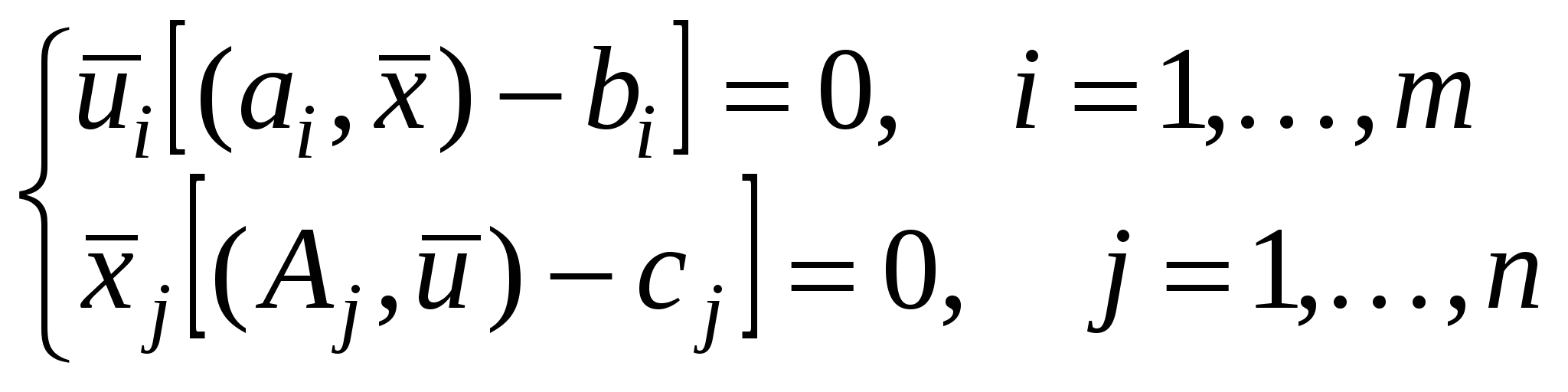– условие дополняющей нежесткости (переменные двойственной задачи умноженные на ограничения прямой, и переменные прямой, умноженные на ограничения двойственной задачи).

1. 
   Если
   
2. 
   Если
   
3. 
   Если
   
4.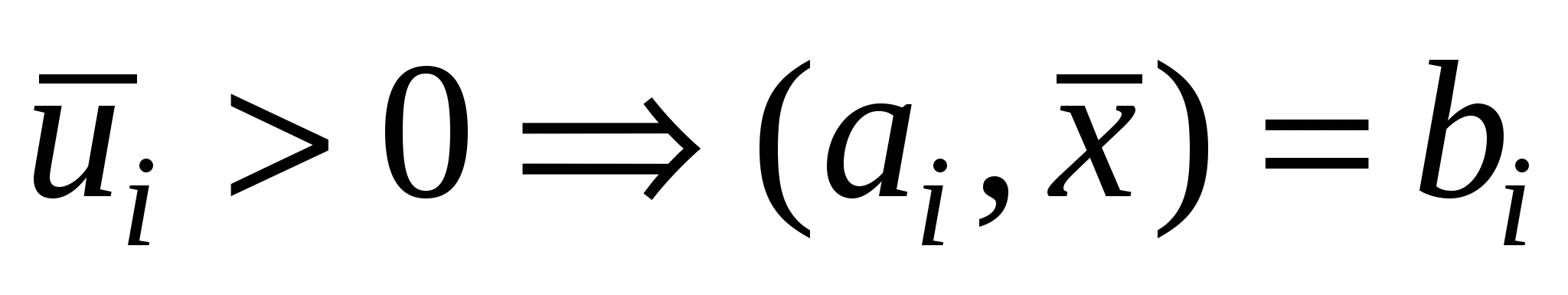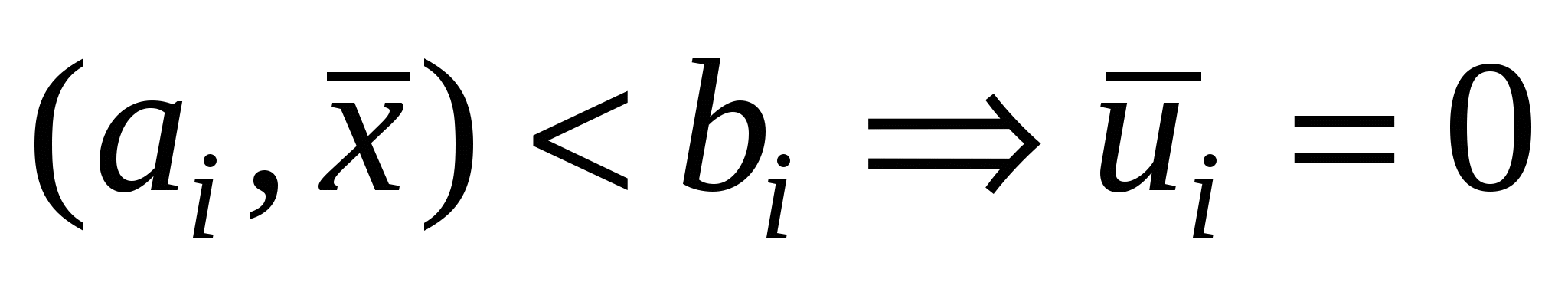 
   Если