Ответы по ЭММ(прошлогодние). 2011г. История возникновения экономикоматематических методов (эмм)

• Название: 2011г. История возникновения экономикоматематических методов (эмм)
• Анкор: Ответы по ЭММ(прошлогодние).doc
• Дата: 04.07.2018
• Размер: 0.5 Mb.
• Имя файла: Ответы по ЭММ(прошлогодние).doc
• Тип: Документы; #21057
• страница: 3 из 3

Экономическая интерпретация условия оптимальности

1. 
   Если оптимальная двойственная оценка i-го ресурса положительна, то при работе по оптимальному плану ресурс используется полностью
   
2. 
   Если при работе по оптимальному плану i-ый ресурс используется не полностью, то оптимальная двойственная оценка = 0 (не влияет на решение)
   
3. 
   Если при работе по оптимальному плану j-ая технология используется, то эта технология не убыточна в ценах (сколько затратили, столько получили)
   
4. 
   Если в ценах j-ая технология убыточна, то при работе по оптимальному плану она не используется.
   

Алгоритм применения условия оптимальности при решении задач ЛП

Дан n-мерный вектор и задача ЛП (L). С помощью условия оптимальности определить, будет ли данный вектор оптимален в задаче (L).

1. 
   Проверяем (принадлежит ли данный вектор множеству допустимых решений задачи L) – подставить в условие задачи, проверить выполнимость ограничений.
   
2. 
   Определить вид множества U – ограничения двойственной задачи
   
3. 
   Написать условие дополняющей нежесткости с подстановкой . Получим систему линейных алгебраических уравнений для определения .
   
4. 
   Решаем эту систему, находим .
   
5. 
   Проверяем (принадлежит ли данный вектор множеству допустимых решений двойственной задачи) – подставить в условие задачи L*, проверить выполнимость ограничений.
   
6. 
   Если да (принадлежит), то – оптимальный в задаче L, если нет (не принадлежит) то не оптимальный в задаче L.
   

16. 
    Свойства закрытой транспортной модели.
    

Транспортная задача: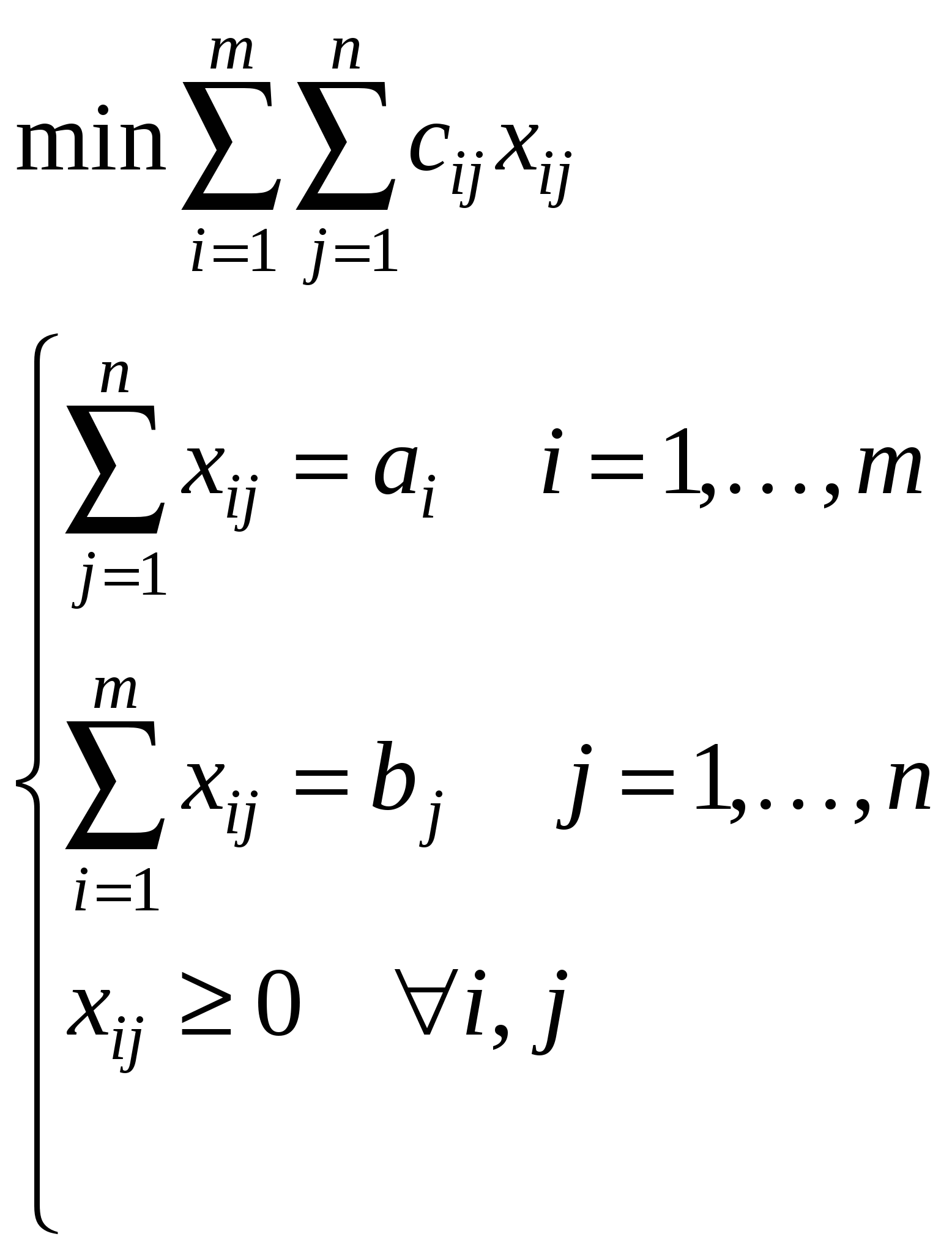



Задача называется закрытой (замкнутой), если выполняется условие баланса: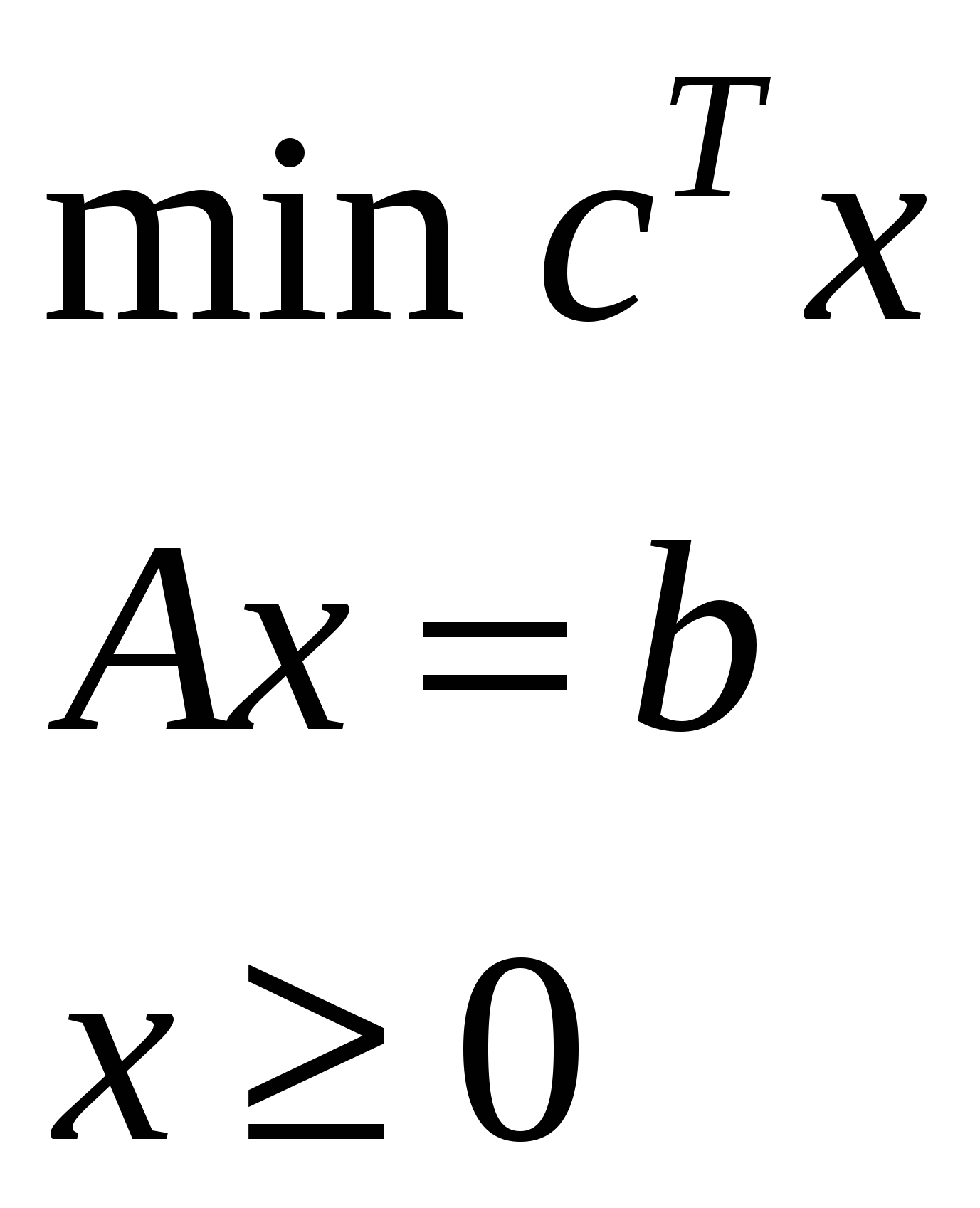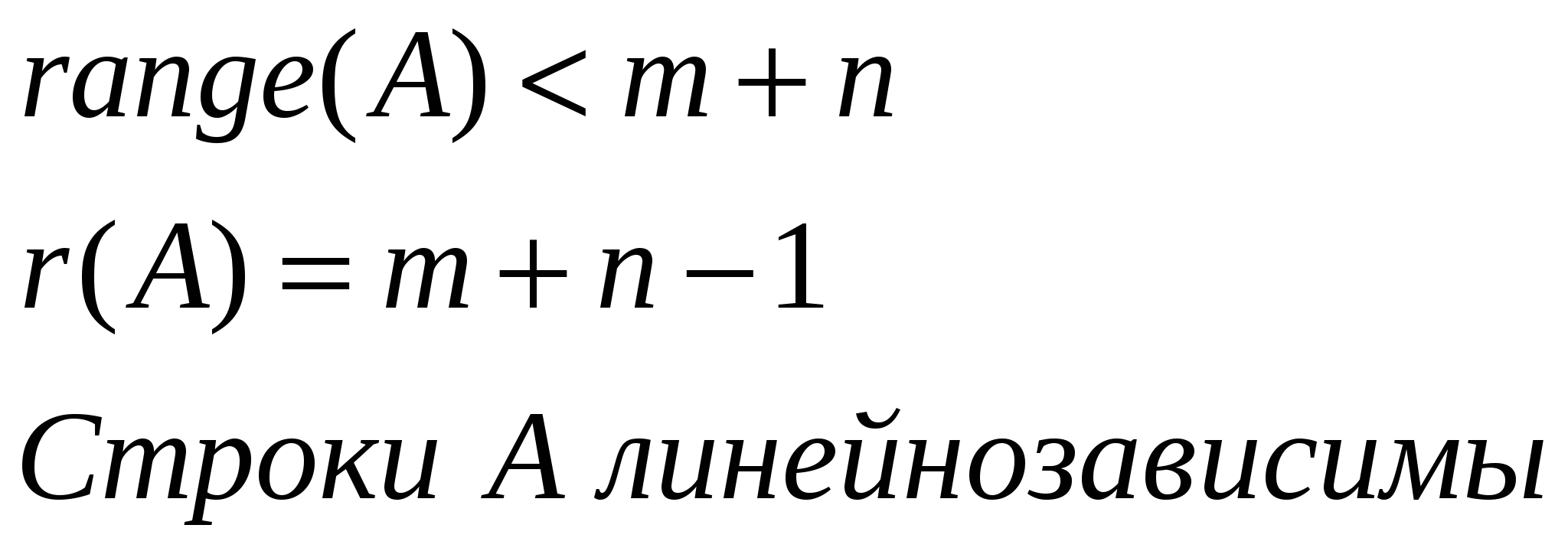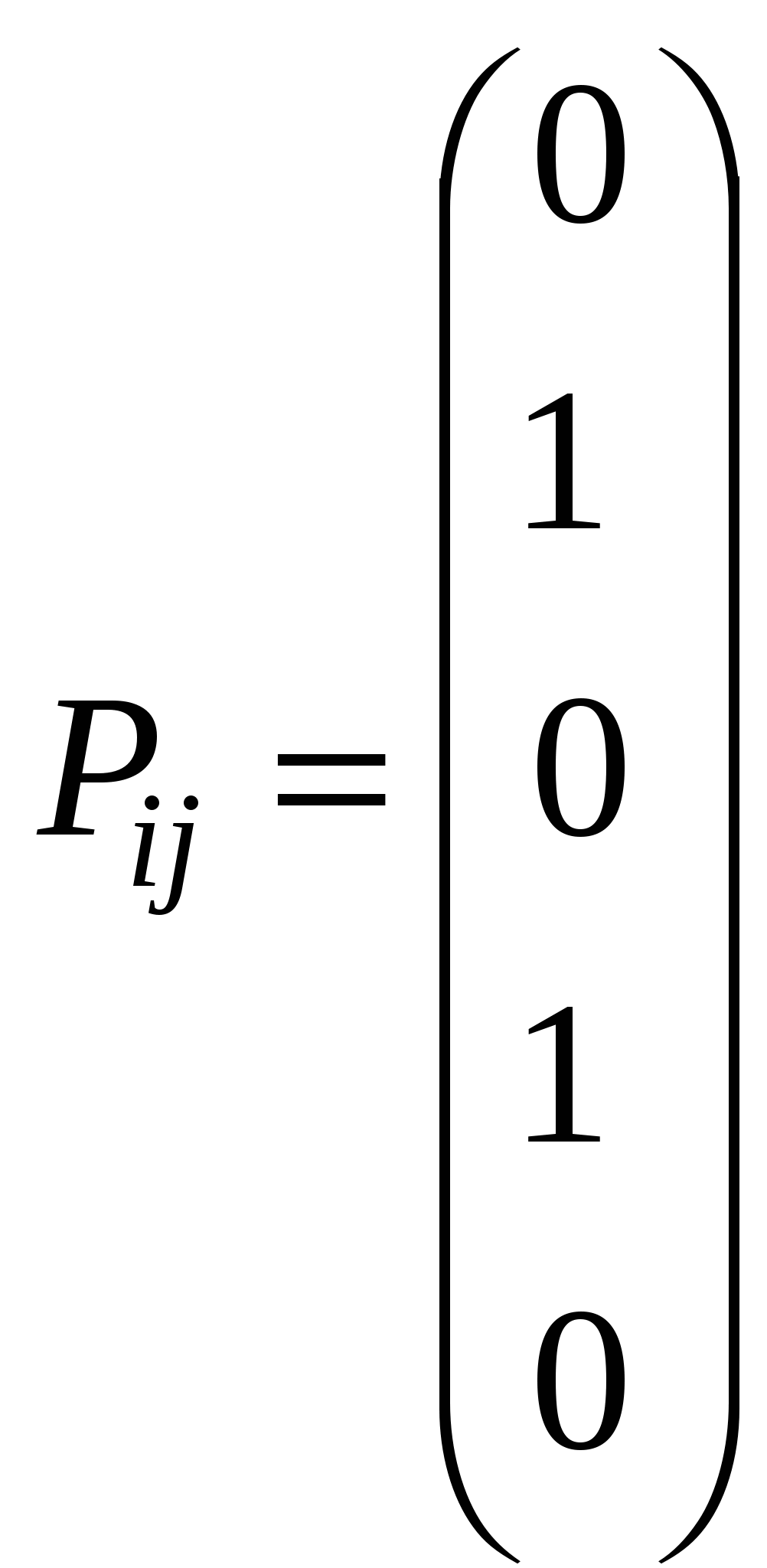

– необходимое и достаточное условие решения задачи
,

, состоит из столбцов, каждый из которых содержит всего две единички:


i

m+j

Двойственная задача для канонической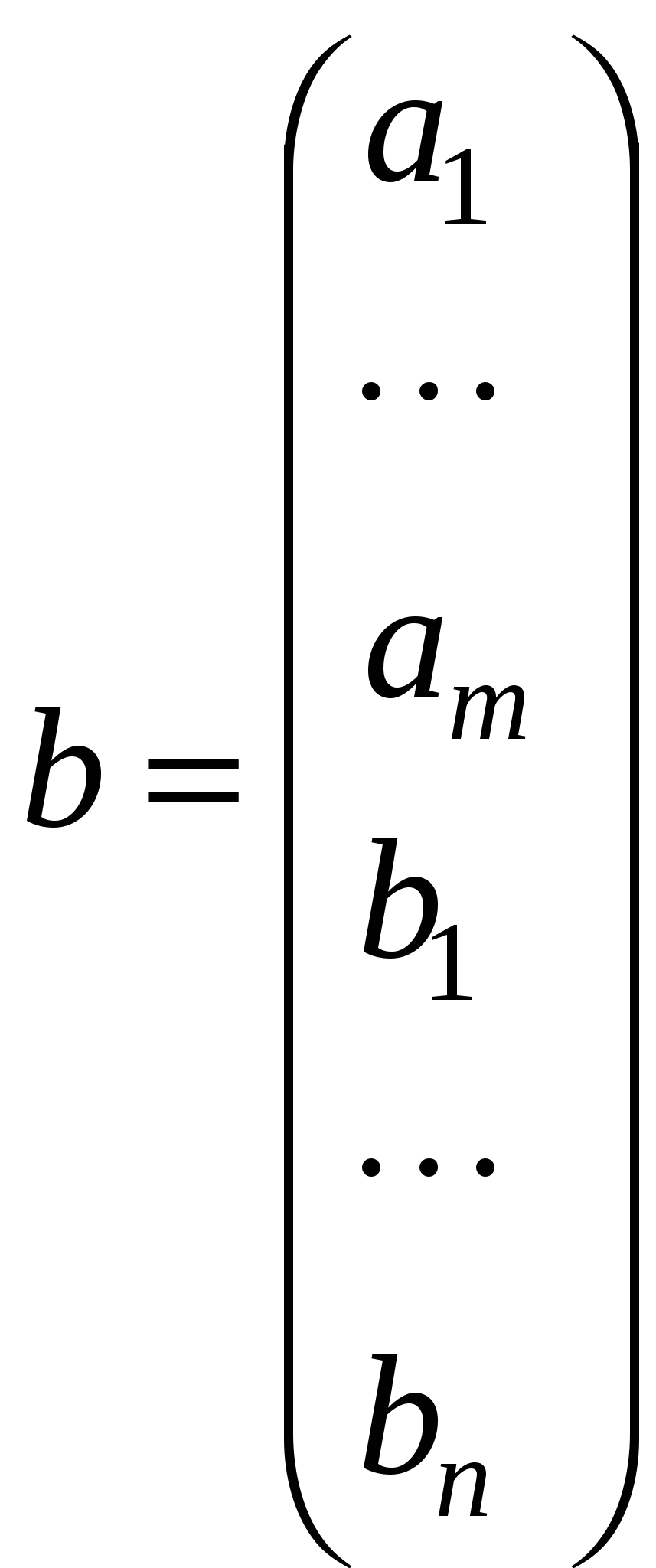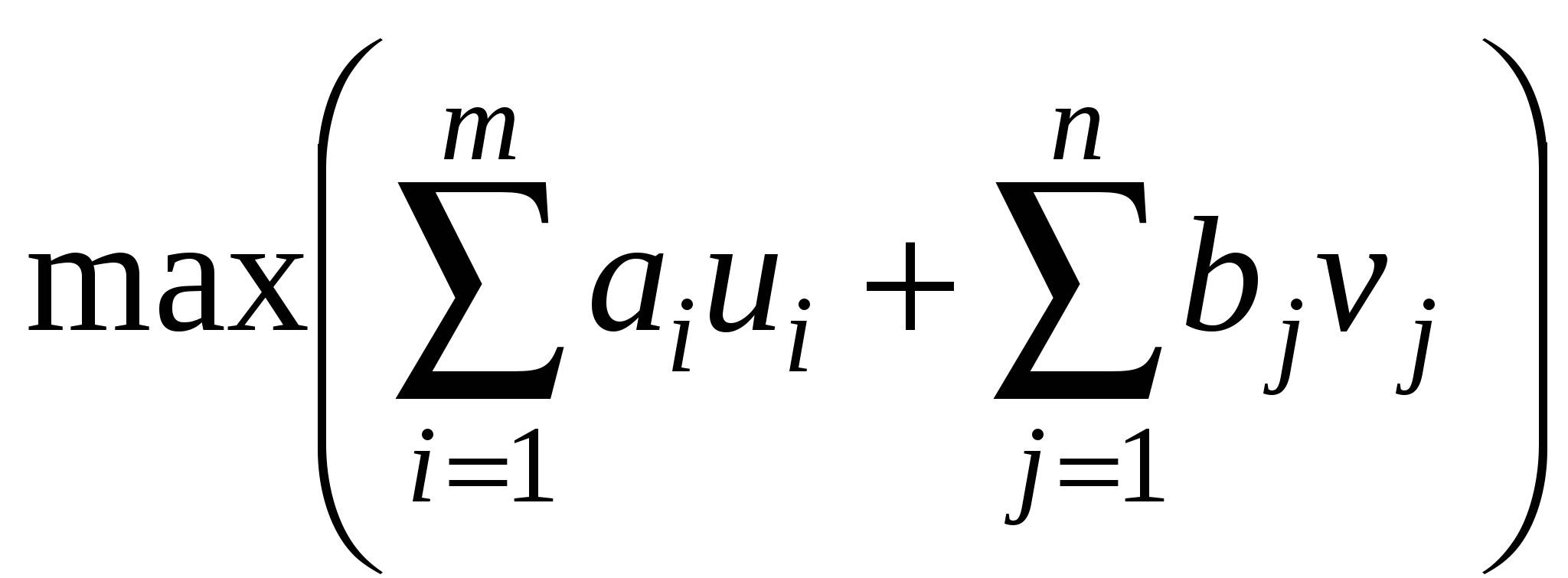








– условие оптимальности в ТЗ



Если задача незамкнута

1. 
   – есть избыток продукции
   

В этом случае вводят фиктивного потребителя, потребности которого составляют разность между количеством существующей продукции и потребностью в ней. Тарифы на перевозку устанавливаются нулевыми для введенного потребителя

2. 
   – есть дефицит продукции, всем не хватит.
   

В этом случае определяют меру штрафа r_j за недоставку j-му потребителю единицы продукции. Затраты увеличиваются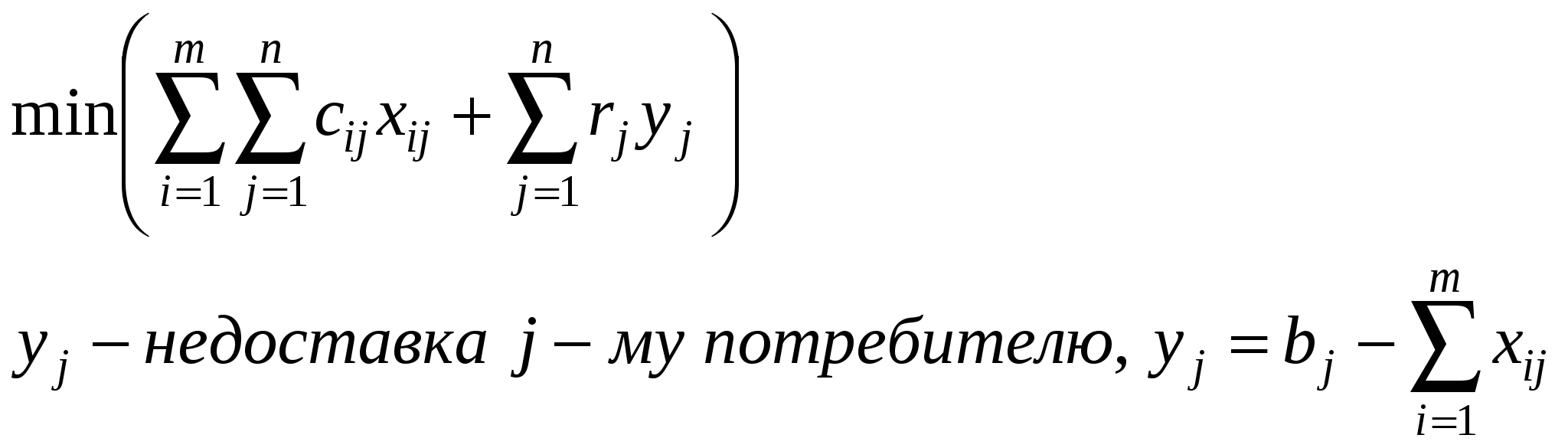



И вводят фиктивного производителя. Тарифы на перевозку от введенного производителя устанавливаются равной мере штрафа



Если предпочтений нет, то штрафы можно установить нулевыми (r_j = 0)

17. 
    Модели транспортного типа.
    

Транспортная задача с запретами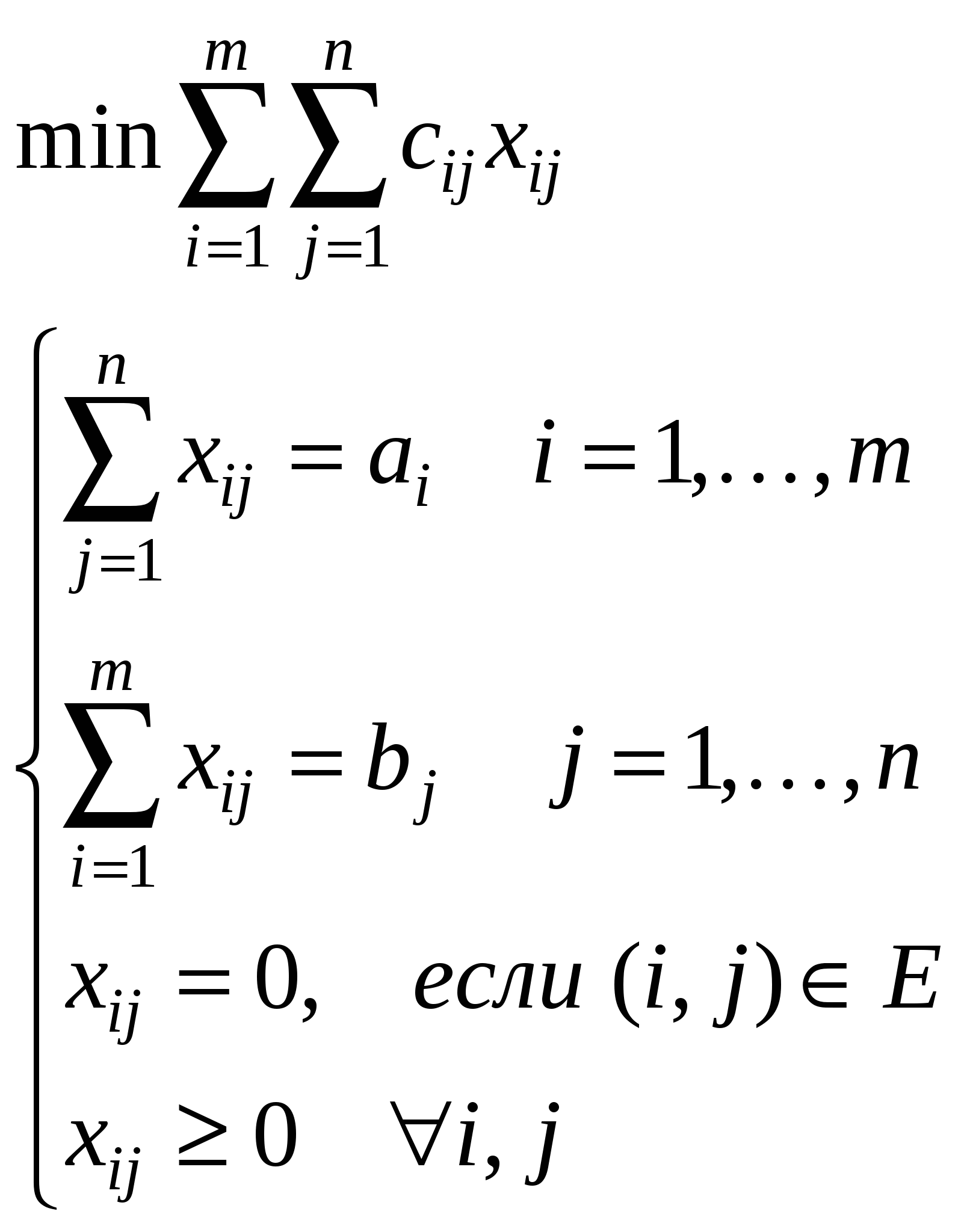

– запреты (не от каждого поставщика к каждому потребителю можно сделать перевозку)



Чем больше запретов, тем сложнее осуществить перевозку и с некоторого момента задача может стать неразрешимой.

В новой задаче (с запретами):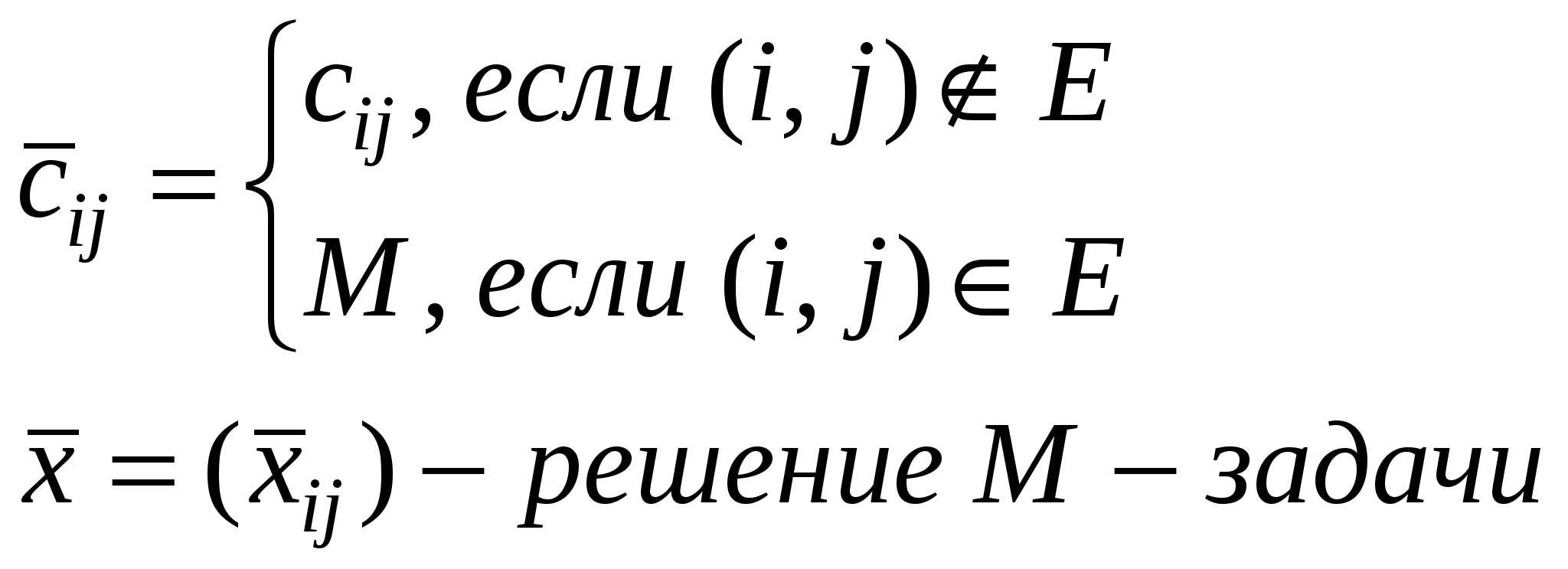

1. 
   – решение задачи с запретами
   
2. 
   задача с запретами не имеет планов
   

Транспортная задача по критерию времени

Из всех возможных маршрутов выбрать тот, у которого самое большое звено будет наименьшим. Вместо стоимости c_ij задается время соответствующей перевозки t_ij.

Целевая функция: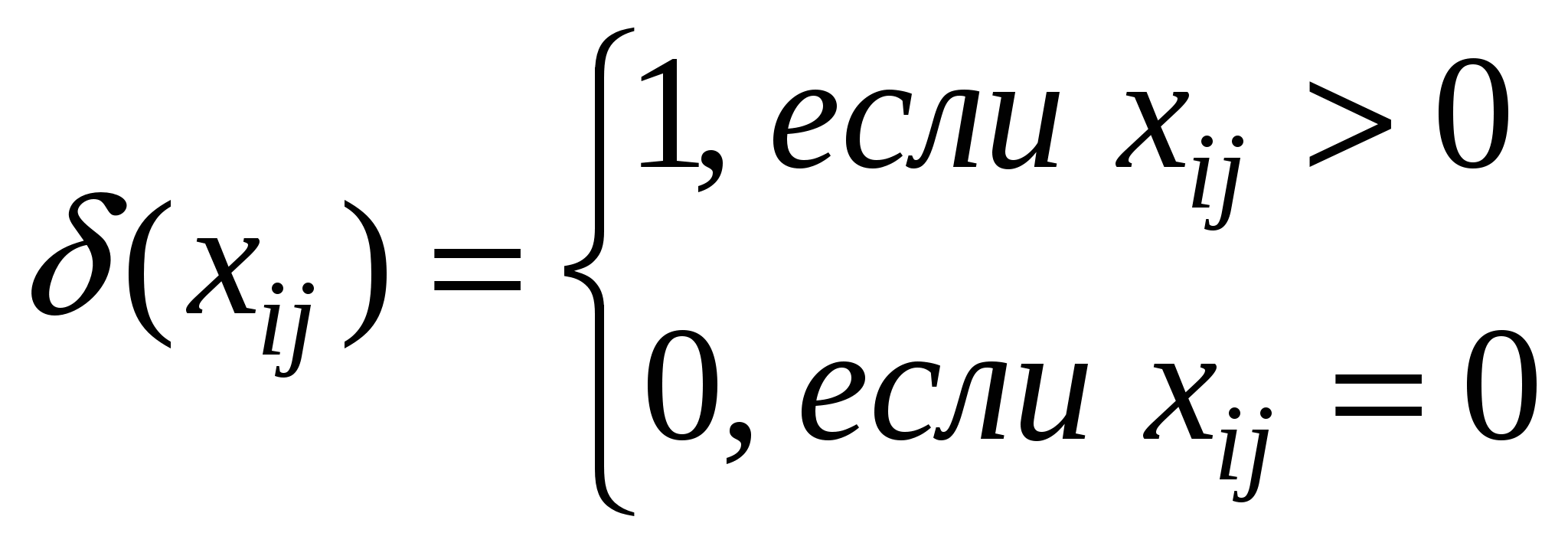





Решение задачи – какое-то t.

Не является задачей линейного программирования, целевая функция – дискретная (не линейная).

18. 
    Распределительные модели.
    

Задача о перевозке взаимозаменяемых продуктов

m пунктов производства топлива
a_i – объём производства i-го сорта топлива, i= 1, …, m

В каждом пункте производится один сорт топлива
n потребителей тепла
b_j – количество тепла, необходимое j-му потребителю, j= 1, …, n

λ_ij – коэффициент перехода от i-го сорта топлива к j-му потребителю. (Сколько килокалорий получается у j-го потребителя при сжиганий i-го сорта топлива)
c_ij – удельные транспортные затраты, стоимость перевозки i-го сорта топлива к j-му потребителю.

Требуется так организовать перевозку, чтобы полностью удовлетворить потребности каждого потребителя в тепле и минимизировать при этом суммарные транспортные издержки.

x_ij – искомый объём перевозки из i-го сорта топлива в j-му потребителю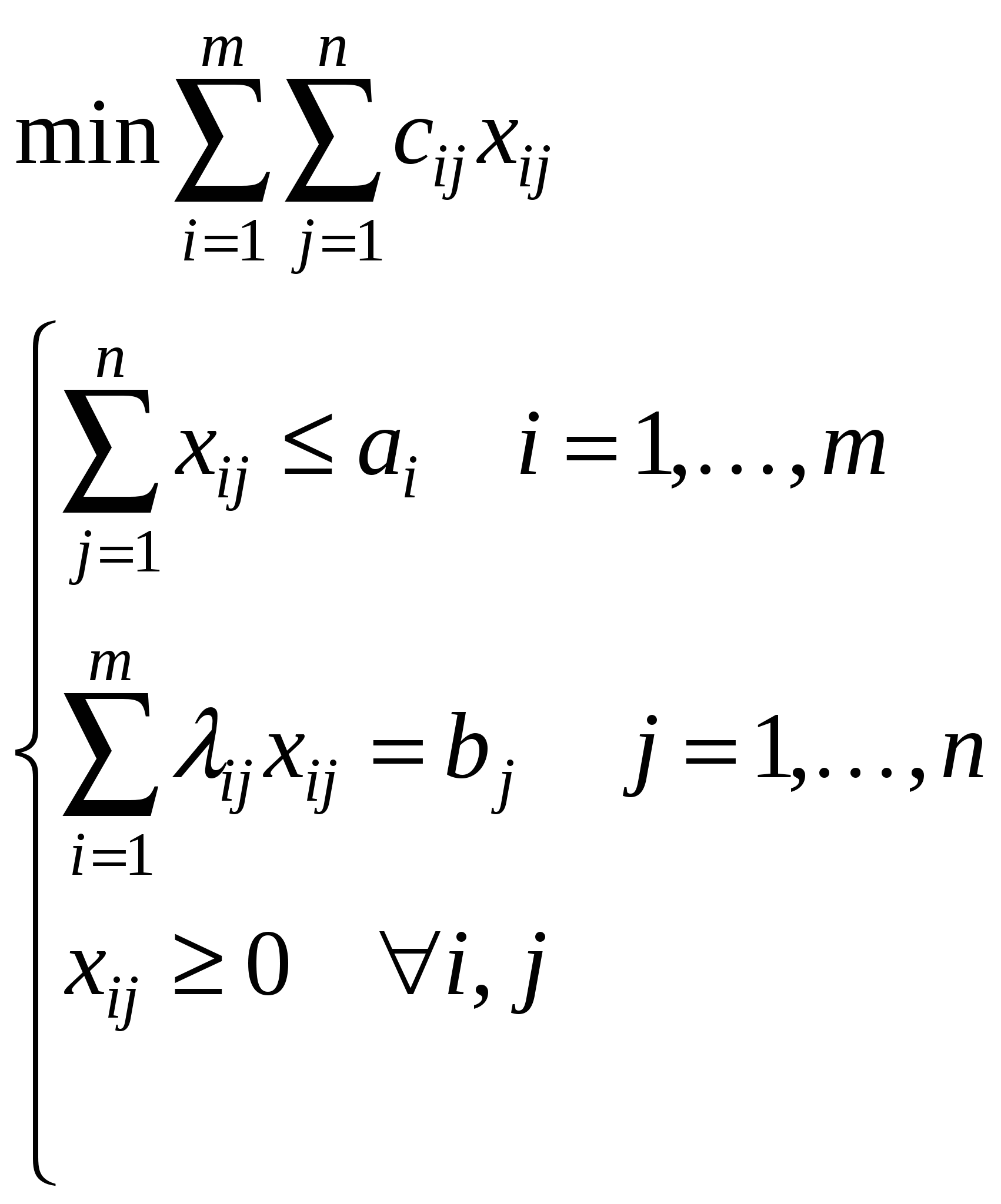

– распределительная задача ЛП
Задача определения производственной задачи предприятия

m изделий нужно изготовить
a_i – план по i-му изделию, i= 1, …, m

n предприятий

T – время выполнения заказа
τ_j – объем работы времени на j-ом предприятии, j= 1, …, n

t_ij – время работы на j-ом предприятии для изготовления 1 единицы i-го изделия.
c_ij – стоимость изготовления 1 единицы i-го изделия на j-ом предприятии.

Требуется так организовать производство, чтобы не выходя за рамки отведенного времени, выполнить заказ с минимальной себестоимостью.

x_ij – количество изделий i-го вида, изготовляемых на j-ом предприятии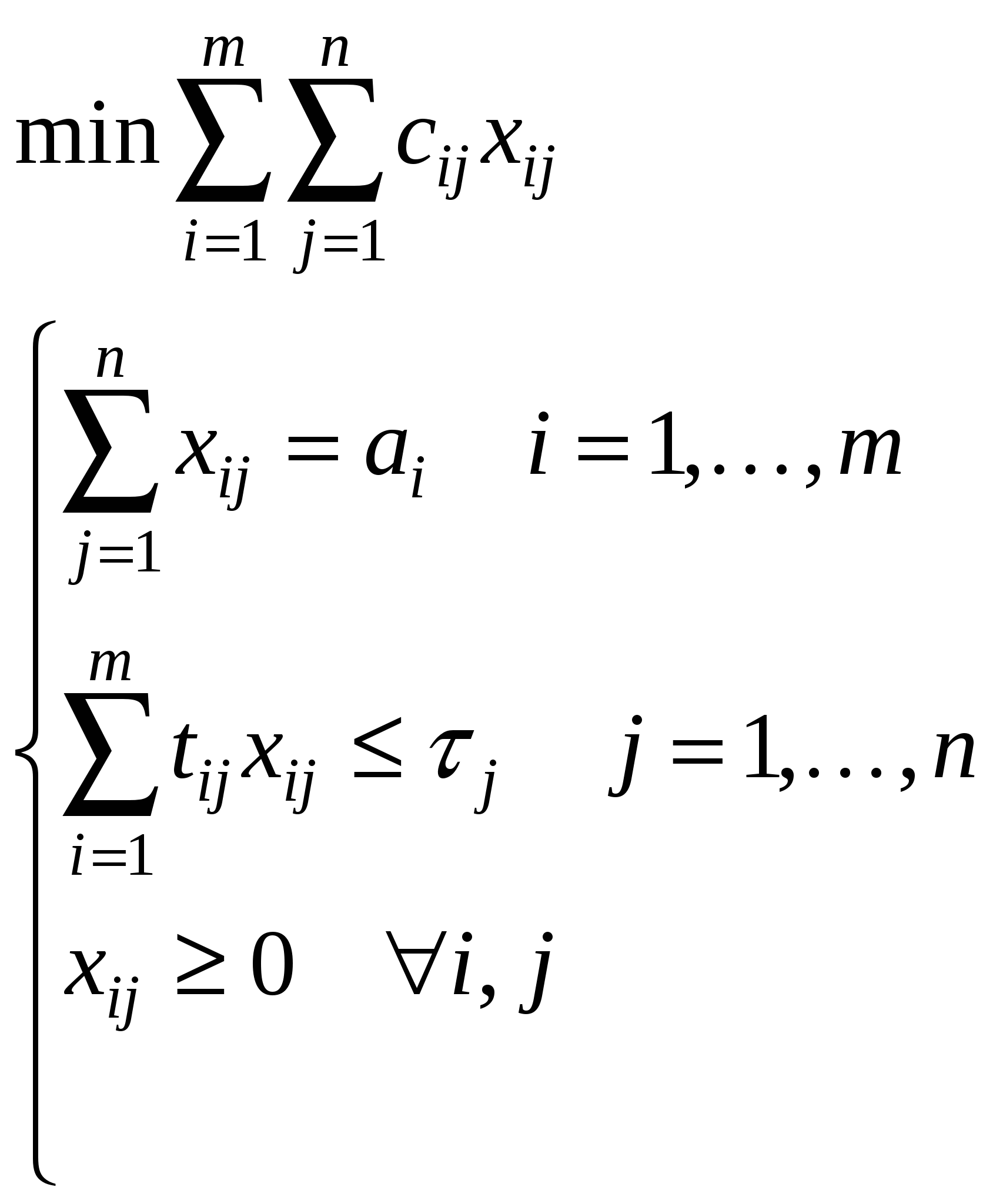



Обозначим: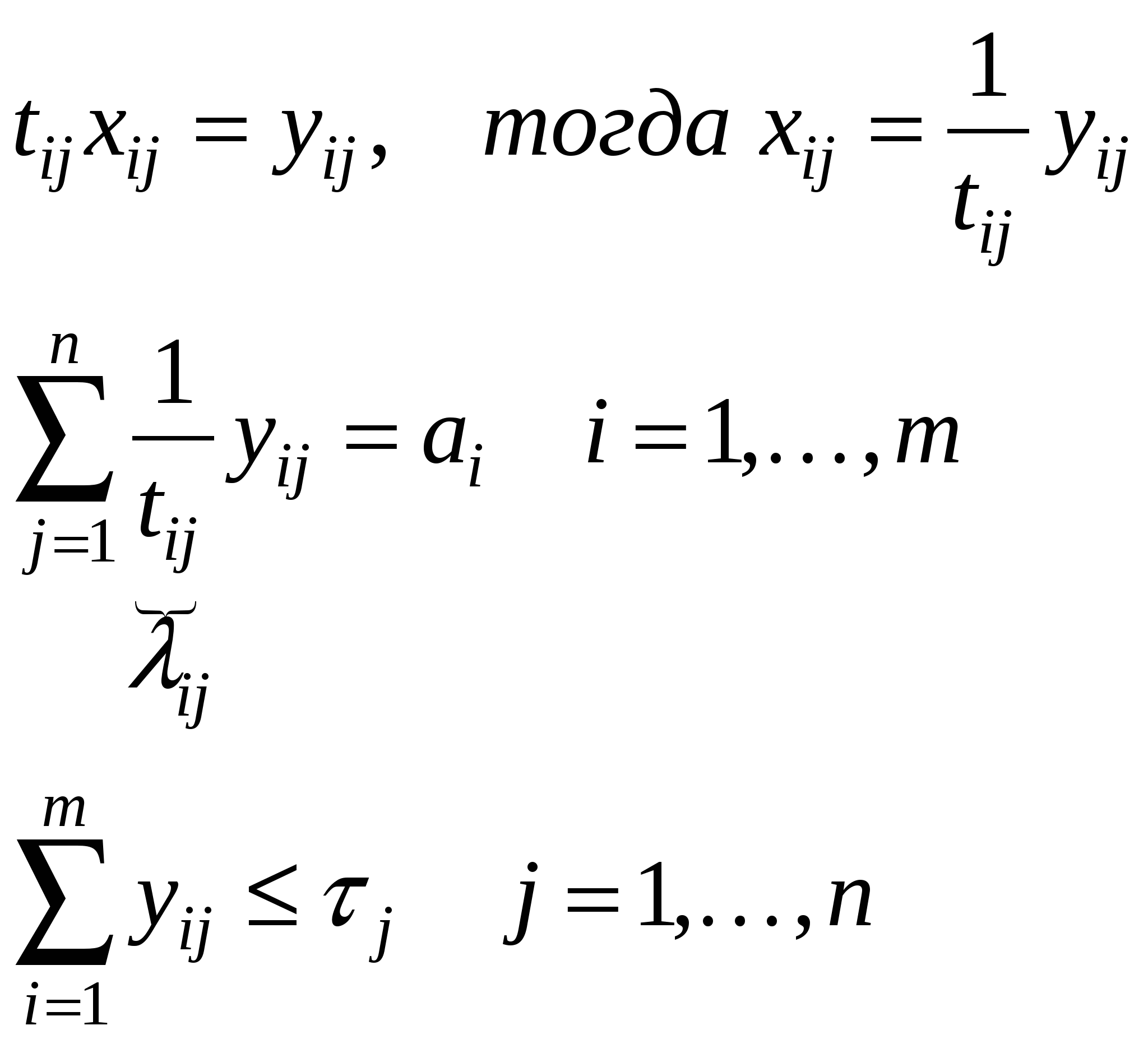

– свели к предыдущей задаче

Если все λ_ij = 1, то получим транспортную задачу.

Если все λ_ij = α_iβ_j (можно представить в виде такого произведения), то можно свести к ТЗ.

В этом случае r(λ_ij)_mxn = 1, r(А) = m + n,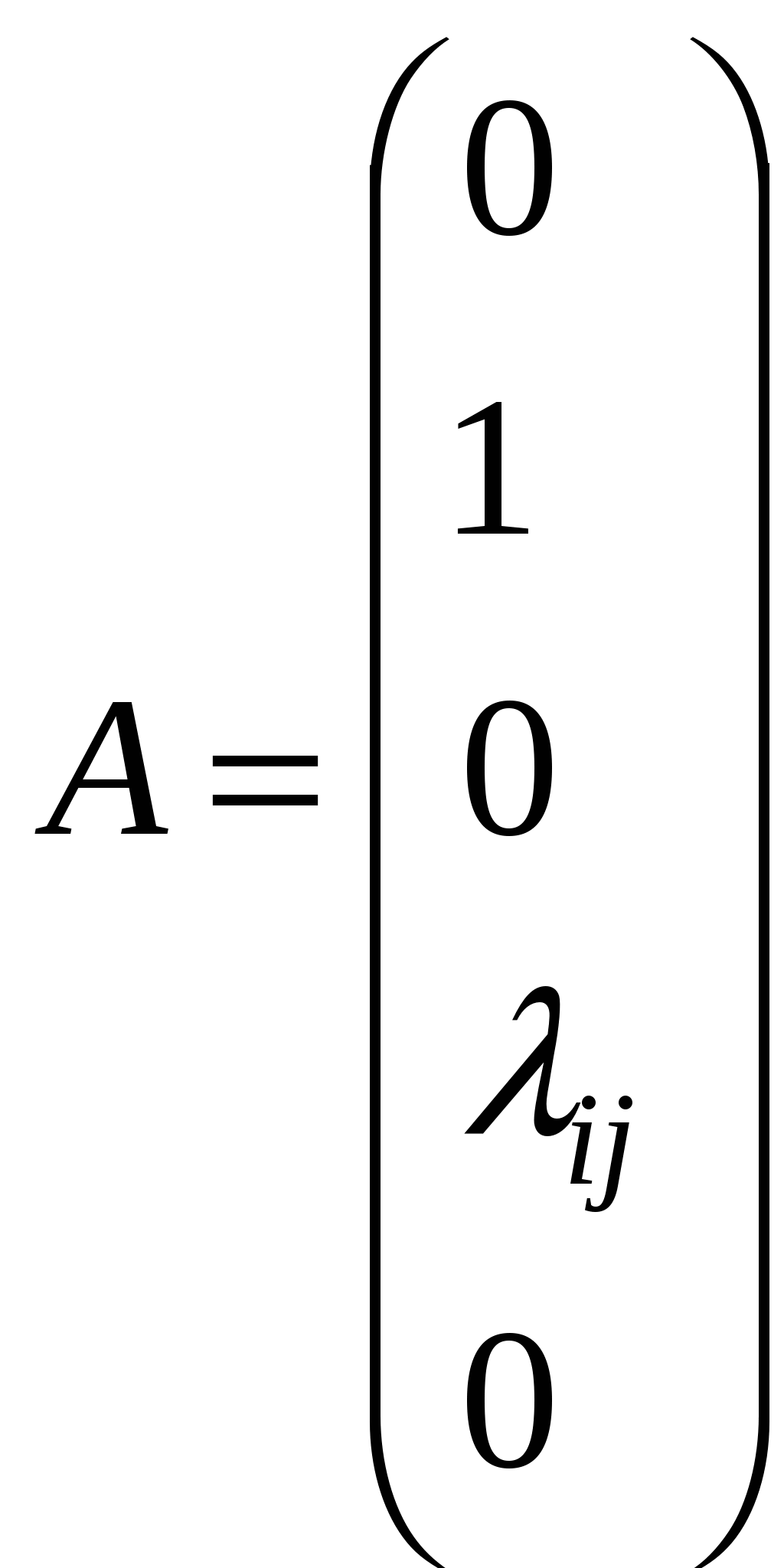

19. 
    Целочисленные линейные модели:
    

Переменные – целые числа.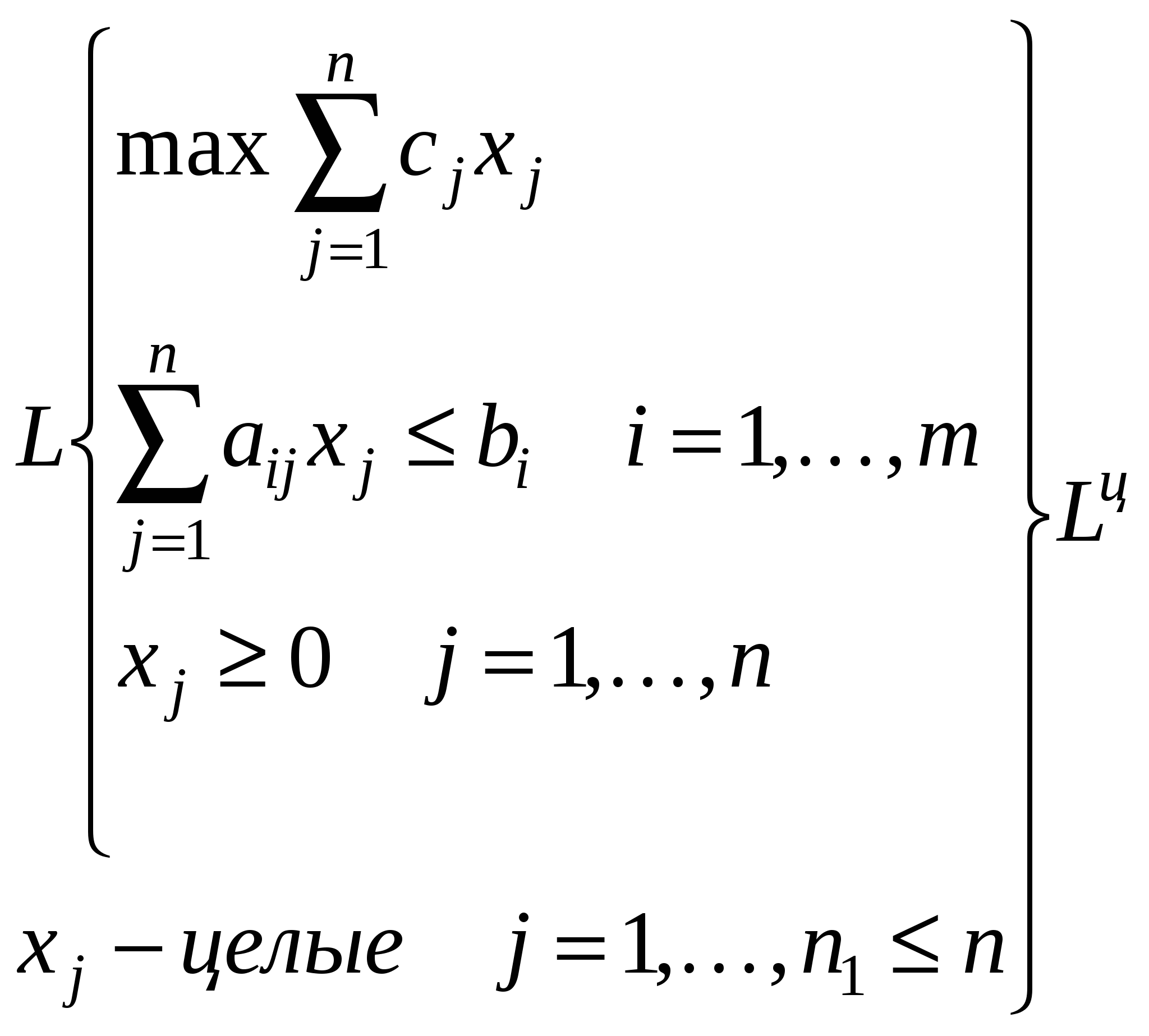

– задача L с условием целочисленности

1. 
   задачи с неделимостями
   

Переменные определяют физически неделимые объекты. Задача о рюкзаке:

n предметов есть в наличии (необязательно разных)
p_j – вес j-го предмета, j= 1, …, n

c_j – ценность j-го предмета,

P – «грузоподъемность» рюкзака.

Требуется загрузить рюкзак набором предметов из данных n с максимальной суммарной ценностью.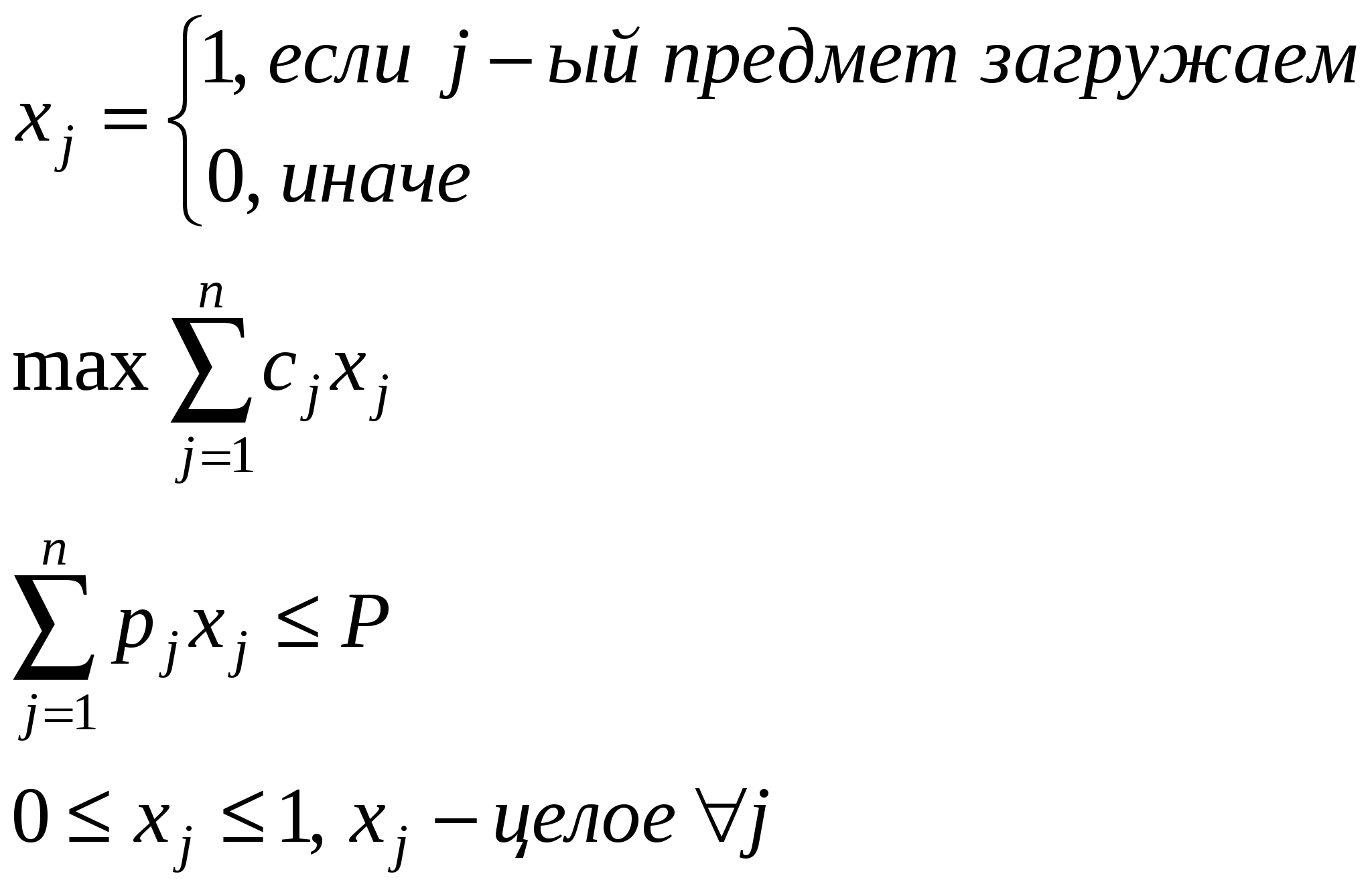


Задача возникает при сборе чумадана в поездку, в инженерном проектировании, при загрузке космических кораблей.

2. 
   задача коммивояжера
   

Есть n + 1 город p₀, p₁, …, p_n. Задана матрица расстояний c_ij = ρ(p_i, p_j).

Коммивояжер выезжая из города p₀, должен объехать все города, побывать в каждом из них ровно по одному разу и вернуться обратно в p₀

Как объехать города так, чтобы пройденное расстояние было минимальным.

Всего возможных маршрутов n(n – 1)…(n – k)…1 = n!, для n = 13: n! = 6 227 020 800, то есть перебор не приемлем. Сводят к задаче целочисленного ЛП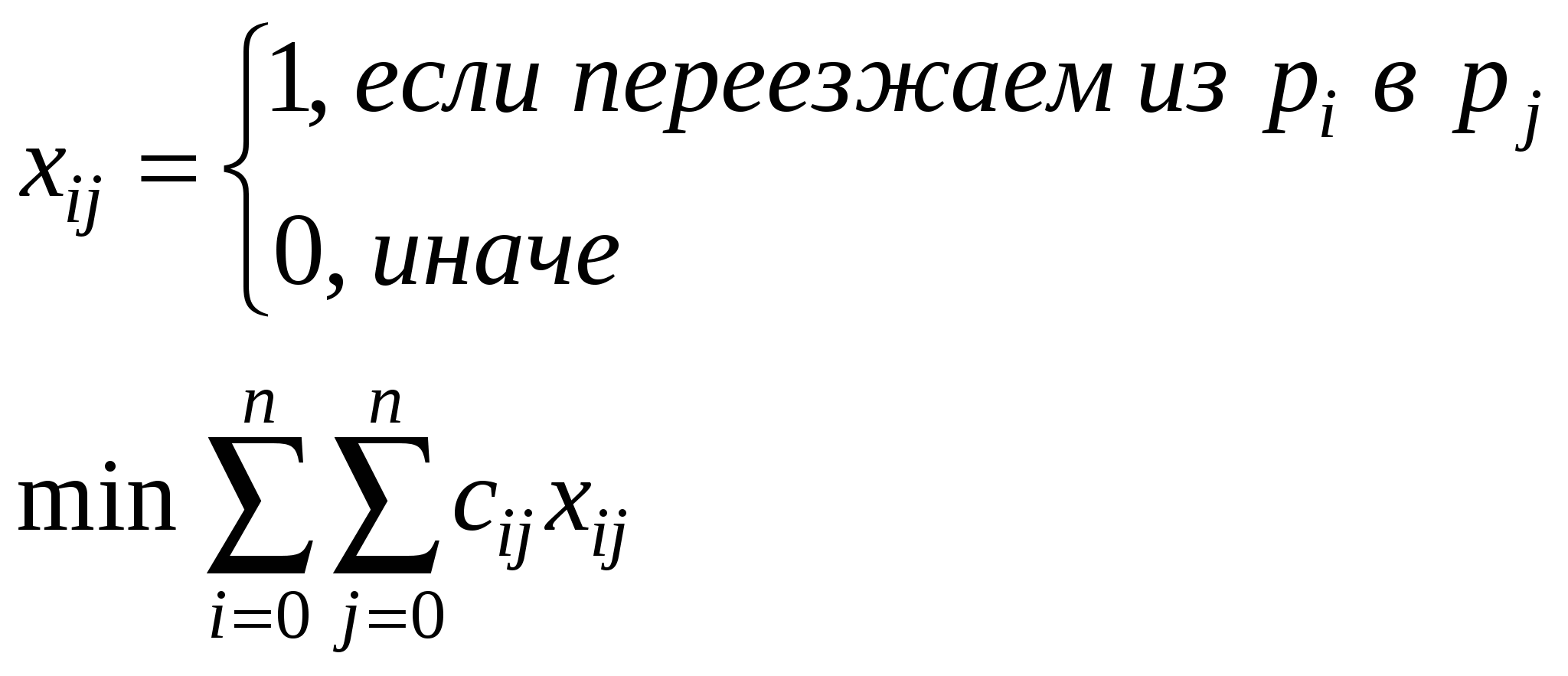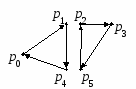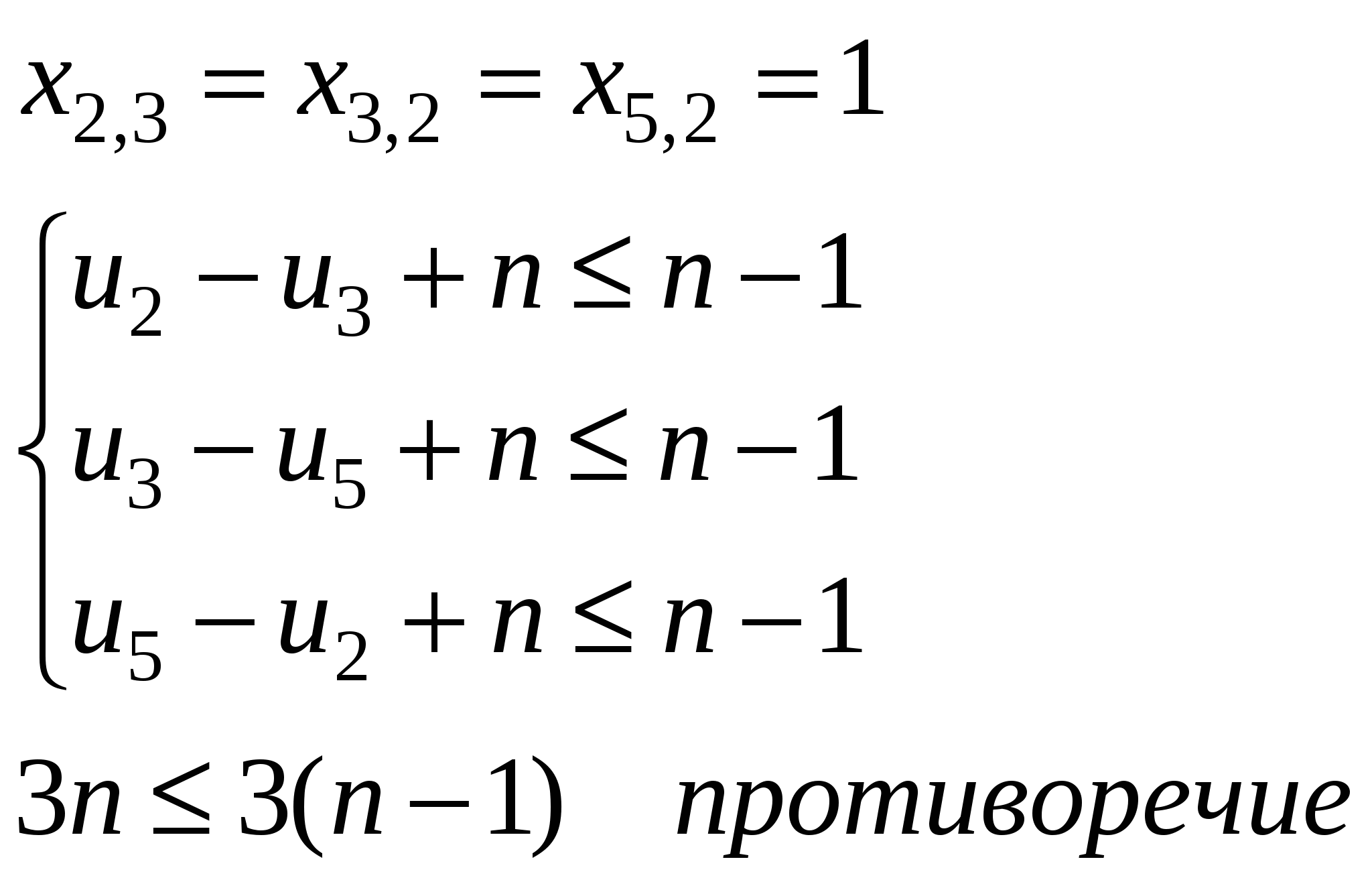



– из p_i можно поехать только в один другой город

– в p_j можно приехать только из одного другого города



– не дает маршруту распасться





u_i = k, если p_i посещается на k-ом шаге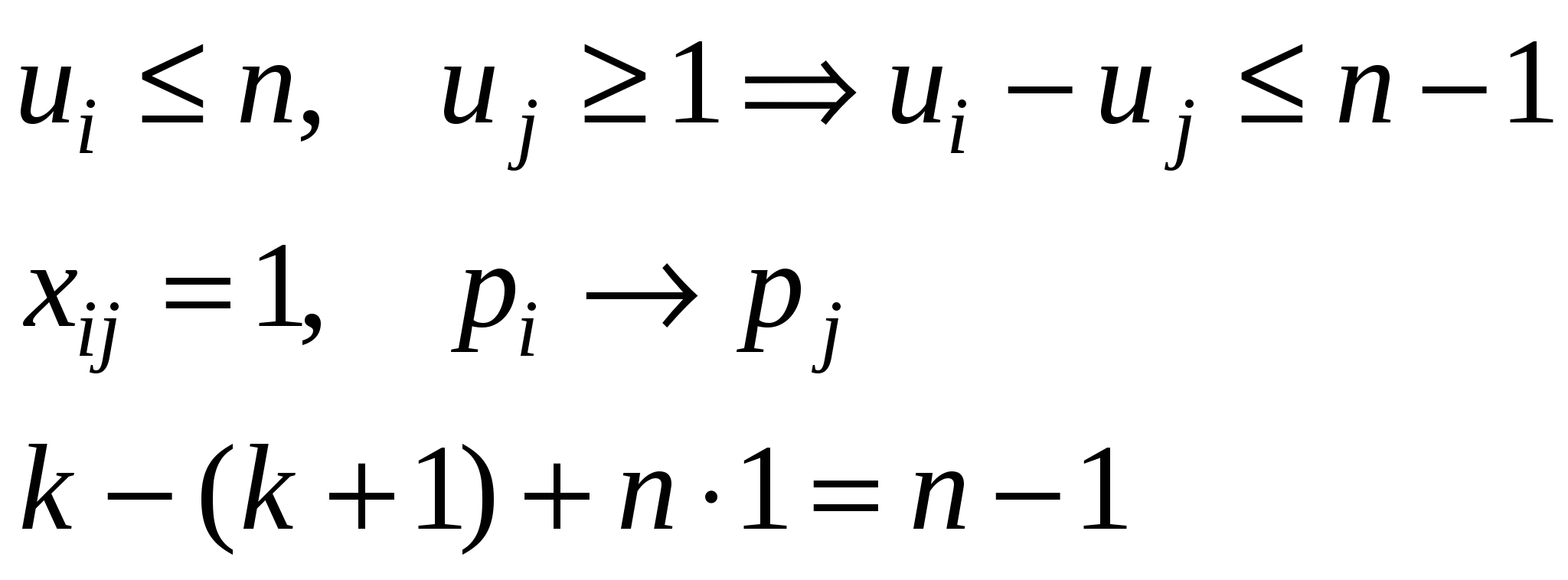



u существует и можно брать из N

3. 
   задача о назначениях
   

n работ

n кандидатов на выполнение.

Требуется распределить работы между кандидатами наиболее рациональным образом.
c_ij – затраты, связанные с назначением i-ой работы j-му кандидату



– i-ая работа может быть назначена только одному кандидату

– j-ый кандидат может выполнять только одну работу



Частный случай транспортной задачи, но сильно вырождена (матрица nx n из n единиц, ранг матрицы r(A) = n – 1)

4. 
   модель рационального раскроя
   

Есть стандартные заготовки. Нужно:

1. 
   Сделать требуемое количество шаблонов (видов деталей)
   
2. 
   Затратить минимум заготовок (или другой вариант – минимизировать отходы)
   

Задачи бывают:

1. 
   Одномерные (трубы, кабель…)
   
2. 
   Двумерные (листы,…)
   
3. 
   Трехмерные
   

Одномерный случай:

L – длина заготовки

m видов детали
a_i – план по детали i, i= 1, …, m

l_i – длина i-ой детали

n – число способов раскроя

a_ij – количество деталей i-го вида, получаемых из одной заготовки, раскраиваемой по способы j.
x_j – количество заготовок, раскраиваемых по способу j.

Ограничения в задаче:	Целевая функция:
	– если нужно затратить минимум заготовок – если нужно минимизировать отходы где