6-7 математика ОТВЕТЫ. 2020 2021 учебный год 6 класс Решения Предметнометодическая комиссия город Новороссийск Задача 1
 Скачать 35.24 Kb. Скачать 35.24 Kb.
|
|
ШКОЛЬНЫЙ ЭТАП Всероссийской олимпиады школьников по математике 2020 -2021 учебный год 6 класс Решения Предметно-методическая комиссия город Новороссийск Задача 1. Инопланетяне сообщили жителям Земли, что в системе их звезды три планеты А, Б, В. Они иживут на второй планете. Далее передача сообщения ухудшилась из-за помех, но было принято еще два сообщения, которые, как установили ученые, оказались оба ложными: а) А – не третья планета от звезды; б) Б – вторая планета. Какими планетами от звезды являются А, Б, В? Решение: Так как второе и третье сообщения ложны, то А является третьей планетой, а Б – не второй, поэтому Б – первая планета от звезды. Тогда В будет второй планетой, на которой живут инопланетяне. Задача 2. На плоскости расположены шесть точек и несколько прямых так, что через любые две точки проходит какая-то из данных прямых, а через каждую точку проходит ровно три из данных прямых. Укажите один из вариантов такого расположения точек и прямых. Решение: пример 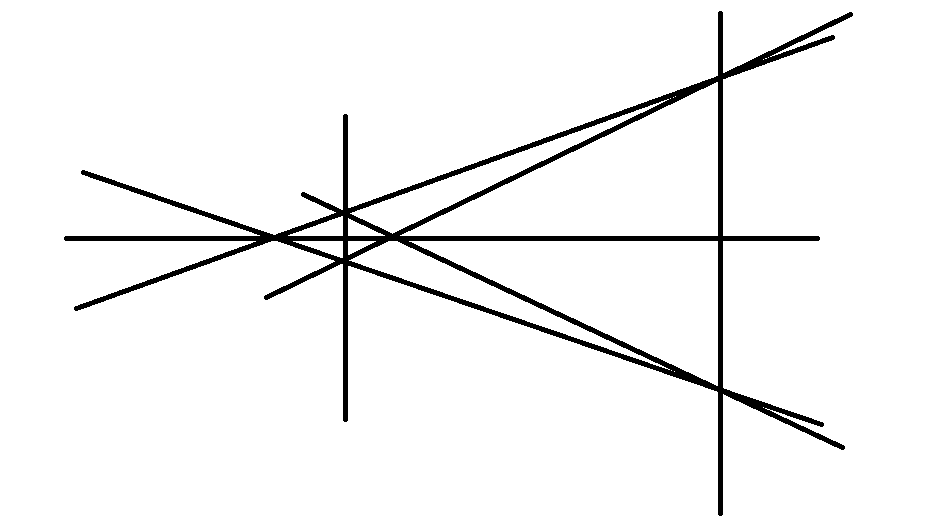 Задача 3. В школе 30 классов и 1000 учащихся. Доказать, что есть класс, в котором не менее 34 ученика. Решение: предположим, что нет класса, в котором не менее 34 ученика. Тогда в каждом классе 33 ученика, а так как классов 30, то всего учеников 30*33=990 < 1000 ШКОЛЬНЫЙ ЭТАП Всероссийской олимпиады школьников по математике 2020 -2021 учебный год 7 класс Решения Предметно-методическая комиссия город Новороссийск Задача 1. Древнегреческая задача: - Скажи мне, знаменитый Пифагор, сколько учеников посещают твою школу и слушают твои беседы? - Вот сколько, - ответил Пифагор, - половина изучает математику, четверть – природу, седьмая часть проводит время в размышлении и , кроме того, есть ещё три женщины. Сколько всего учеников посещает школу Пифагора? Решение: Решается с помощью уравнения: 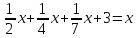 . Ответ: 28 учеников. . Ответ: 28 учеников.Задача 2. Можно ли квадрат разрезать на несколько тупоугольных треугольников? Решение: Можно. Пример 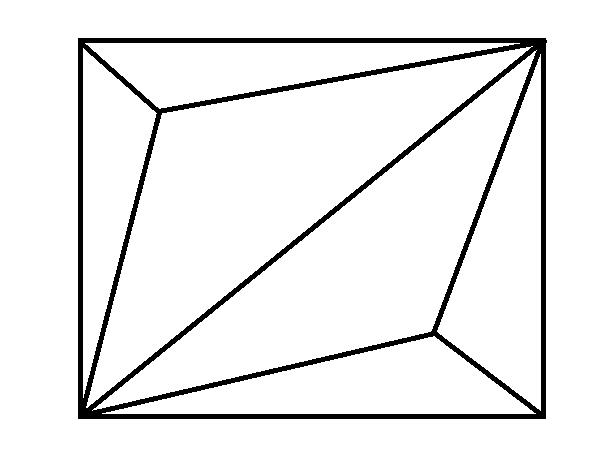 Задача 3. Найдите все натуральные числа a, b, c и d, для которых справедливо равенство: 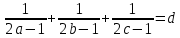 Решение: Каждое слагаемое слева не больше 1 и поэтому 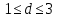 , причем, , причем, 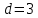 лишь в случае, когда все слагаемые равны 1, то есть лишь в случае, когда все слагаемые равны 1, то есть 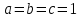 . Если . Если 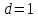 , то каждое слагаемое слева меньше 1, а значит, не больше , то каждое слагаемое слева меньше 1, а значит, не больше 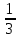 , поэтому равенство возможно лишь когда слагаемые равны по , поэтому равенство возможно лишь когда слагаемые равны по 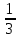 , то есть , то есть 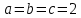 . Замечаем, что . Замечаем, что 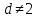 , так как после приведения к общему знаменателю слева получим дробь с нечетным числительным. , так как после приведения к общему знаменателю слева получим дробь с нечетным числительным. Окончательно находим только два набора чисел: 1; 1; 1; 3 и 2; 2; 2; 1 |
