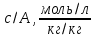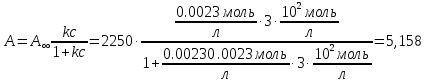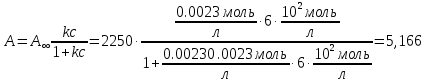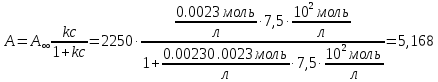Коллоидная химия. задачи. 3 кгм3, если шарообразные частицы суспензии имеют дисперсность 2106 м
 Скачать 116.01 Kb. Скачать 116.01 Kb.
|
|
127. Определите величину удельной поверхности суспензии каолина (плотность равна 2,5·103 кг/м3), если шарообразные частицы суспензии имеют дисперсность 2·106 м-1. Суспензию считайте монодисперсной. Ответ дайте в м-1 и в м2/кг. Определите, к какому типу (согласно принятым классификациям) относится дисперсная система Дано: ρ = 2,5·103 кг/м3 D= 2·106 м-1 Решение: удельная поверхность (Sуд) – отношение общей (межфазной) поверхности (мфп) Sмфп к объему Vф или массе ωф диспергированной фазы: 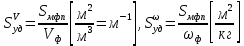 1.Находим удельную поверхность суспензии каолина как отношение мфп к объему диспергированной фазы по следующей формуле: 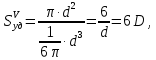 где D – дисперсность, м-1. 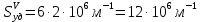 2. Находим удельную поверхность суспензии каолина как отношение мфп к массе диспергированной фазы по следующей формуле: 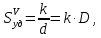 где k – коэффициент формы, тогда 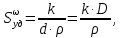 kдля сферических, кубических частиц = 6 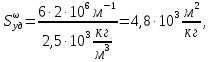 3. Удельная поверхность гетерогенной системы связана с дисперсностью и размерами частиц выражением: 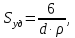 Поскольку частицы дисперсной фазы имеют шарообразную форму, находим их диаметр по следующей формуле: 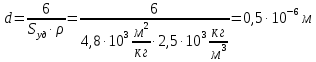 Диаметр частицы равен 0,5·10-6 м, следовательно, согласно классификации а) по дисперсности: система относится к группе ультрамикрогетерогенных систем (d < 1 мкм); б) по агрегатному состоянию фазы и среды: каолин – это твердое нерастворимое в воде соединение, следовательно, с водой образует систему типа Т/Ж (гидрозоль или коллоидный раствор), а в газообразной среде – Т/Г (аэрозоль); в) по взаимодействию частиц дисперсной фазы – свободнодисперсная система (частицы подвижны, участвуют в броуновском движении, равномерно распределяются в объеме системы); г) по взаимодействию фазы и среды – лиофобная коллоидная система (каолин нерастворим в воде, поэтому требуется принудительное диспергирование). Ответ 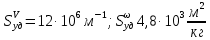 146. Вычислите коэффициент растекания по воде для бензола и анилина, если работа когезии для бензола равна 0,0577 Дж/м2, для анилина равна 0,0832 Дж/м2, а работы адгезии соответственно равны 0,0666 и 0,1096 Дж/м2. Объясните различие в коэффициентах растекания. Дано: WA (бензол) = 0,0666 Дж/м2 WK (бензол) = 0,0577 Дж/м2 WA (анилин) = 0,1096 Дж/м2 WK (анилин) = 0,0832 Дж/м2 Решение: Растекание возможно при условии, что работа адгезии будет больше работы когезии: Wа ≥ Wк. Адгезионные силы характеризуют молекулярное взаимодействие между поверхностями воды и бензола/анилина и стремятся растянуть каплю, тем самым увеличивая поверхность раздела «вода – бензол/анилин». В то же время силы когезии, действующие внутри капли бензола/анилина, стягивают ее, препятствуя растеканию, и результат смачивания будет зависеть от соотношения работ адгезии и когезии. Разность работ адгезии и когезии Wа – Wк называется коэффициентом растекания по Гаркинсу, f. Если f > 0 – жидкость растекается, при f < 0 жидкость на межфазной поверхности не склонна к растеканию 1. Коэффициент растекания по воде для бензола f (бензол) = 0,0666 Дж/м2 – 0,0577 Дж/м2 = 0,0089 Дж/м2 > 0, следовательно бензол растекается по воде. 2. Коэффициент растекания по воде для анилина f (анилин) = 0,1096 Дж/м2 – 0,0832 Дж/м2 = 0,0264 Дж/м2 > 0, следовательно анилин растекается по воде. Коэффициенты растекания для бензола и анилина различны, поскольку данная величина связана со строением жидкостей и с характером ориентации их молекул на границе раздела фаз и для каждого вещества своя. Ответ: f (бензол) = 0,0089 Дж/м2; f (анилин) = 0,0264 Дж/м2. 176. Вычислите поверхностное натяжение толуола при 323 К, если методом наибольшего давления пузырька газа получены следующие данные: давление пузырька при проскакивании его в воду равно 14,28·102 Н/м2, а в толуол составляет 5,03·102 Н/м2. Поверхностное натяжение воды при 323 К равно 67,91·10-3 Н/м. Дано: 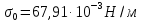  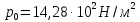 Решение: По мере роста пузырька воздуха, выдуваемого в жидкость через капилляр, радиус кривизны поверхности пузырька уменьшается до радиуса капилляра, а внешнее избыточное давление растет и становится максимальным 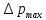 и равным капиллярному (лапласовскому) давлению: и равным капиллярному (лапласовскому) давлению: 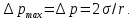 Это выражение используют для определения поверхностного натяжения 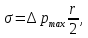 Для двух объектов (при условии постоянства параметров эксперимента) соблюдается соотношение 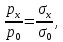 где 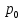 и и 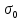 – давление и поверхностное натяжение воды. Поверхностное натяжение толуола рассчитываем по уравнению – давление и поверхностное натяжение воды. Поверхностное натяжение толуола рассчитываем по уравнению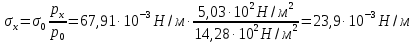 Ответ: поверхностное натяжение толуола равно 23,9 мН/м. 187. Определите проекцию среднего сдвига 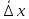 для частиц гидрозоля за время 10 с, если радиус частиц 0,05 мкм, температура опыта 293, вязкость среды 1⋅10-3 Па⋅с. для частиц гидрозоля за время 10 с, если радиус частиц 0,05 мкм, температура опыта 293, вязкость среды 1⋅10-3 Па⋅с.Дано: T = 293 K τ = 10 с η = 1⋅10-3 Па⋅с = 1⋅10-3 Н⸱с/м2 r = 0,05 мкм = 0,05⸱10-6 м Решение: 1. Среднеквадратичный сдвиг связан с коэффициентом диффузии уравнением Эйштейна – Смолуховского Δх2 = 2Dτ, где Δх – средний сдвиг частицы, м/с D – коэффициент диффузии, м2/с τ – время наблюдения, с 2. Коэффициент диффузии вычислим по уравнению Эйнштейна 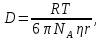 где NА – число Авогадро, 6,02 · 10 23 молекул/моль; η – вязкость дисперсионной среды, Н · с/м2 (Па · с); r – радиус частицы, м; R – универсальная газовая постоянная, 8,314 Дж/моль · К; T – абсолютная температура, К. 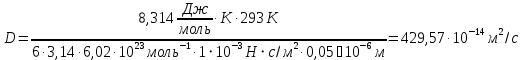 3. Рассчитаем проекцию среднего смещения (среднеквадратичный сдвиг) частиц эмульсии 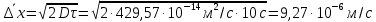 Ответ: 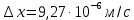 208. С помощью метода поточной ультрамикроскопии в объеме 3∙10-12 м3 подсчитано 55 частиц аэрозоля – дыма мартеновских печей. Частицы имеют кубическую форму с длиной ребра куба 92 нм, плотность 2∙103 кг/м3. Определите концентрацию частиц аэрозоля. Дано: n = 55 l = 92 нм ρ = 2∙103 кг/м3 V= 3∙10-12 м3 Решение: 1. Объем одного кубика золота равен: V0 куб l3 → V0 куб=(92 нм)3=7,79⸱10-22м3 2. Учитывая, что масса частиц дисперсной фазы m в видимом объеме V равна m = c⸱V; масса одной частицы m0будет равна 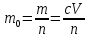 , объем одной частицы равен , объем одной частицы равен 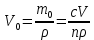 , находим концентрацию частиц , находим концентрацию частиц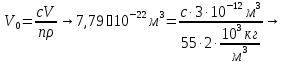 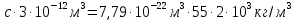 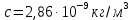 Ответ: концентрация частиц аэрозоля 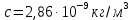 230. Коллоидный раствор (золь) Cr(OH)3 получен при смешивании 10 мл водного раствора CrCl3 с молярной концентрацией 0,01 моль/л и 16 мл водного раствора NH4OH с молярной концентрацией 0,02 моль/л. 1) Напишите уравнение реакции и определите, какой из продуктов реакции образует золь. 2) Рассчитайте, какое из исходных веществ – CrCl3 или NH4OH – взято в избытке. 3) Напишите формулу мицеллы образовавшегося золя Cr(OH)3 и укажите заряд коллоидной частицы (гранулы). 4) Определите, к какому электроду и какая часть мицеллы будет перемещаться при электроосмосе. 5) Для данных электролитов: K2SO4, NaNO3, Na3PO4, MgCl2, CdSO4, Al2(SO4)3: а) определите, какой из ионов электролита будет вызывать коагуляцию, и расположите ионы в ряд в порядке уменьшения порога коагуляции; б) рассчитайте пороги коагуляции Ск в золе Cr(OH)3 для каждого из предложенных электролитов, используя правило Шульца-Гарди или закономерность Дерягина-Ландау, если порог коагуляции гидрозоля Cr(OH)3 под действие электролита KNO3 равен Ск. Решение: 1. Согласно реакции CrCl3 + 3 NH4OH = Cr(OH)3 + 3 NH4Cl гидрозоль образует Cr(OH)3, так как плохо растворяется в воде. 2. Рассчитываем, какое из исходных веществ взято в избытке, для этого находим число моль эквивалентов каждого из исходных веществ nэк(В) = V·Cм·Z, где V – объем раствора, л; См – молярная концентрация, моль/л; Z – число эквивалентности вещества Z(CrCl3) = 1; nэк (CrCl3) = 10·10–3·0,01·1 = 1·10–4 моль; Z(NH4OH) = 4 nэк (NH4OH) =16·10–3·0,02·4 = 12,8·10–4 моль. В избытке взят NH4OH. Так как NH4OH взят в избытке, следовательно, раствор NH4OH будет являться электролитом-стабилизатором, ионы которого образуют ДЭС: NH4OH →NH4+ + OH- 3. В соответствии с правилом Фаянса-Панета-Пескова, ионы NH4+ будут являться потенциалопределяющими ионами, тогда ионы OH- – противоионами. 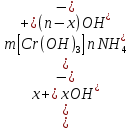 4. Потенциалопределяющими ионами являются NH4+. В растворе протекает реакция, приводящая к образованию золя гидроксида хрома (III). Ядро мицеллы будет представлено агрегатом из m молекул Cr(OH)3, на поверхности которых в соответствии с правилом Панета-Фаянса адсорбируются ионы (потенциалопределяющие), входящие в состав агрегата и находящиеся в избытке. Заряд ядра компенсируется противоионами, часть которых прочно удерживается у поверхности адсорбционными и электростатическми силами (образуется гранула). Другая часть противоионов вследствие теплового движения распределяется в диффузной части ДЭС. Мицелла нейтральна, а коллоидная частица положительна и при электрофорезе будет перемещаться к отрицательно заряженному электроду. Коагулирующими ионами для данного золя будут анионы, так как при увеличении концентрации их в системе ДЭС сжимается. 5. а) Коагуляцию положительно заряженного гидрозоля хрома вызывают противоионы, т. е. анионы электролитов. NaNO3, MgCl2, K2SO4, CdSO4, Na3PO4, Al2(SO4)3 б) Соотношения порогов коагуляции разнозарядных ионов электролитов по Дерягину-Ландау равны: Ск(1) : Ск(2) : Ск(3) = 1:0,016:0,0014. Электролит KNO3 содержит 1 ион–коагулятор 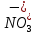 в молекуле KNO3, следовательно: в молекуле KNO3, следовательно:Ск(1) = Ск(KNO3) = 5,0∙10-2 моль/л Электролит–коагулятор K2SO4 содержит 1 ион–коагулятор 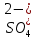 в молекуле K2SO4, следовательно: в молекуле K2SO4, следовательно:Ск (K2SO4) = Cк (2) = Ск(1)⸱0,016 = 5,0∙10-2 моль/л ⸱0,016 = 8∙10-4 моль/л Электролит–коагулятор NaNO3 содержит 1 ион–коагулятор 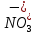 в молекуле NaNO3, следовательно: в молекуле NaNO3, следовательно:Ск (NaNO3) = Ск(1) = Ск(1)⸱1 = 5,0∙10-2 моль/л Электролит–коагулятор Na3PO4 содержит 1 ион–коагулятор 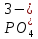 в молекуле Na3PO4, следовательно: в молекуле Na3PO4, следовательно:Ск (Na3PO4) = Ск(3) = Ск(1) ⸱0,0014 = 7⸱10-4 моль/л Электролит–коагулятор MgCl2 содержит 2 ион–коагулятор 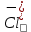 в молекуле MgCl2, следовательно: в молекуле MgCl2, следовательно:Ск (MgCl2) = 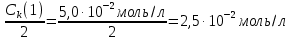 Электролит–коагулятор CdSO4 содержит 1 ион–коагулятор 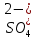 в молекуле CdSO4, следовательно: в молекуле CdSO4, следовательно:Ск (CdSO4)= Ск (K2SO4) = 8∙10-4 моль/л Электролит–коагулятор Al2(SO4)3 содержит 3 ион–коагулятор 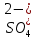 в молекуле Al2(SO4)3, следовательно: в молекуле Al2(SO4)3, следовательно:Ск (Al2(SO4)3)= 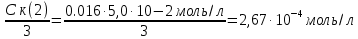 Аналогичные расчеты можно сделать, используя правило Шульце-Гарди. Соотношение порогов коагуляции по Шульце-Гарди Ск(1) : Ск(2) : Ск(3) = 1 : 0,05 : 0,0028; Ск (K2SO4) = Cк (2) = Ск(1)⸱0,05 = 5,0∙10-2 моль/л ⸱0,05 = 2,5∙10-3 моль/л Ск (NaNO3) = Ск(1) = Ск(1)⸱1 = 5,0∙10-2 моль/л Ск (Na3PO4) = Ск(3) = Ск(1) ⸱0,0028 = 1,4⸱10-4 моль/л Ск (MgCl2) = 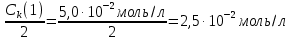 Ск (CdSO4)= Ск (K2SO4) = 2,5∙10-3 моль/л Ск (Al2(SO4)3)= 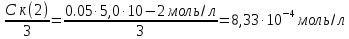 Ответ: 1) заряд коллоидной частицы – положительный; 2) при электрофорезе гранула перемещается к отрицательно заряженному электроду; 3) коагулирующим ионом является анион. По Дерягину-Ландау порог коагуляции уменьшается в следующем ряду: NaNO3, MgCl2,K2SO4, CdSO4, Na3PO4, Al2(SO4)3 По Шульце-Гарди: NaNO3, MgCl2,K2SO4, CdSO4, Al2(SO4)3, Na3PO4 247. По экспериментальным данным адсорбции фенола на ионите при 473 К графически определите: а) константы уравнения Фрейндлиха и Ленгмюра; б) запишите уравнения Фрейндлиха и Ленгмюра с учетом полученных констант; в) пользуясь константами уравнения Ленгмюра, постройте изотерму адсорбции Ленгмюра:
Решение. I) Линейной формой уравнения Фрейндлиха является логарифмическая форма: lgA = lnK+(1/n)lgс. Находим lgс и lgA:
2) Строим график в координатах lgA – lgС и находим по данной зависимости постоянные уравнения: 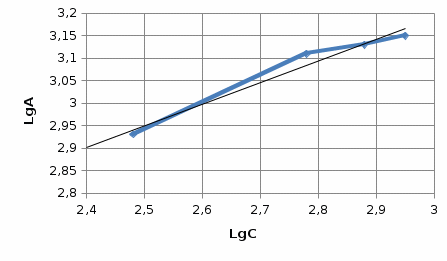 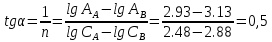 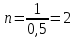 Отрезок ɑ представляет собой lgК в уравнении A= Кc 1/n, Из графика следует, что lg К = 1,75, тогда K = 101,75=56.23 Для данного случая уравнение A= Kc1/n, можно записать так: A= 56.23c2. II) Для построения изотермы адсорбции Ленгмюра в линейных координатах рассчитаем отношение c/А для каждого значения c:
1)По полученным значениям строим изотерму адсорбции в координатах линейной формы уравнении Лэнгмюра:  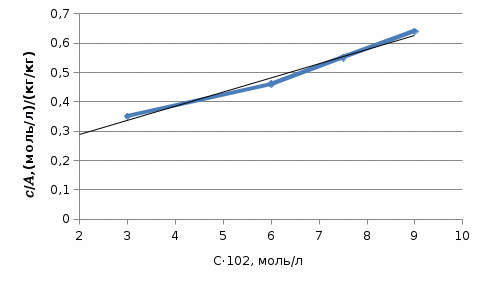 2) Графически рассчитываем константы уравнения Ленгмюра: 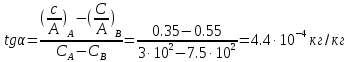 2) Находим значение предельной адсорбции 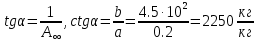 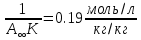 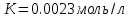 4) Рассчитываем величину адсорбции:
5) Строим изотерму адсорбции Ленгмюра: 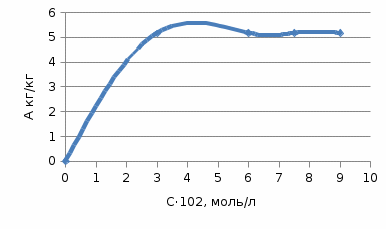 Ответ: а) константы уравнения Фрейндлиха: K = 101,75=56.23; n=2 константы уравнения Ленгмюра: 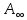 =2250 кг/кг; К=0,0023 моль/л =2250 кг/кг; К=0,0023 моль/лб) Для данного случая уравнение Фрейндлиха A= Kc1/n, можно записать так: A= 56.23c2.  Для данного случая уравнение Ленгмюра: Для данного случая уравнение Ленгмюра: 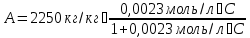 274. Известно, что при образовании насыщенного слоя ПАВ на границе раствор – газ площадь, занимаемая одной молекулой ПАВ, составляет 28(А0)2, толщина адсорбционного слоя – 19,4 А. Плотность ПАВ 930 кг/м3. Рассчитайте молекулярную массу ПАВ. Дано: S0= 28(А0)2 = 2,8 нм2 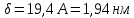 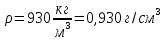 1. Зная площадь, занимаемую молекулой ПАВ в насыщенном слое, рассчитываем величину предельной адсорбции Amax: 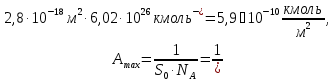 где S0 - площадь, занимаемая одной молекулой, м2; где NА – число Авогадро, 6,02· 10 26 молекул/кмоль; 2. Молекулярная масса ПАВ 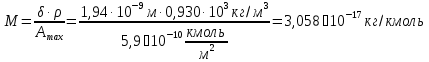 Ответ: М= 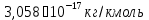 289. По изотерме БЭТ адсорбции бензола при 293 К рассчитайте удельную поверхность адсорбента, если площадь, занимаемая одной молекулой бензола, равна S0 = 0,49 нм2.
Решение данной задачи заключается в обработке данных по уравнению полимолекулярной адсорбции. Для начала необходимо найти значения 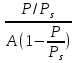 и заполнить табл. и заполнить табл.
Строим зависимость 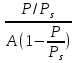 = f (p/ps) = f (p/ps)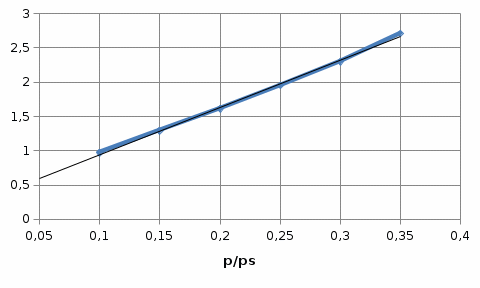 Определяем тангенс угла наклона по координатам двух точек на прямой и отрезок, отсекаемый на оси ординат, что позволит рассчитать значений предельной адсорбции: 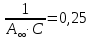 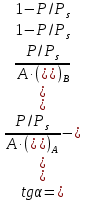 Решаем систему из двух неизвестных 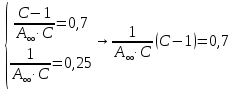 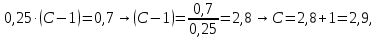 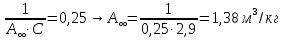 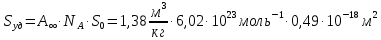 =4,07⸱105 м2/кг =4,07⸱105 м2/кгОтвет: 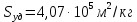 311. По экспериментальным данным конденсации паров воды на активированном угле при Т = 293 К построить: 1) кривую капиллярной конденсации, 2) интегральную и 3) дифференциальную кривые распределения объема пор адсорбента по радиусам (мольный объем адсорбата vm = 0,018 м3/моль; σ = 72,5⸱ 10-3 Дж/м2).
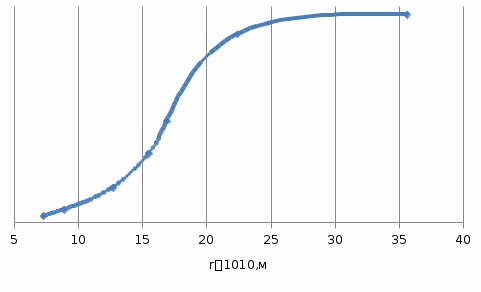
Решение: 1. В соответствии с условием задачи строим изотерму капиллярной конденсации. Капиллярно-конденсационный гистерезис можно наблюдать на изотермах адсорбции в мезопористых материалах при снятии кривых адсорбции-десорбции. При повышении давления пара на пористом адсорбенте идут процессы адсорбции и капиллярной конденсации, при уменьшении давления пара – процессы десорбции и испарения капиллярного конденсата, которые могут сопровождаться капиллярно-конденсационным гистерезисом. Физическая адсорбция обратима и за гистерезис на изотермах сорбции -десорбции ответственна капиллярная конденсация. 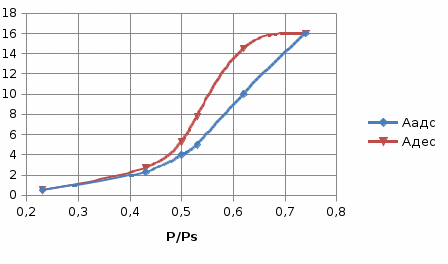 Наблюдается несовпадение ветвей адсорбции и десорбции (гистерезисная петля), вызванное капиллярной конденсацией. 2. Выбрать ряд точек на ветви десорбции (6 – 8), соответствующих определенным значениям p/pS и а) по уравнению V = AVmрассчитать объем пор, заполненных конденсатом; б) для тех же значений p/pSпо уравнению 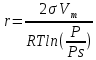 рассчитать максимальный радиус пор, заполненных конденсатом. рассчитать максимальный радиус пор, заполненных конденсатом.
3) Построить интегральную (структурную) кривую адсорбента в координатах V = f(r) (кривая 1). 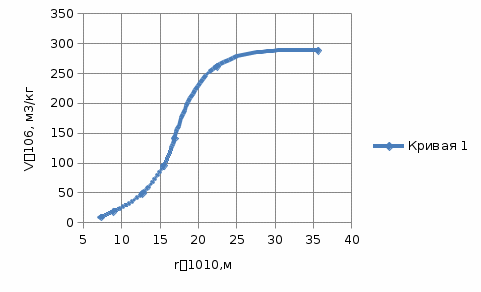 4) Пользуясь интегральной кривой распределения объема пор по радиусам найти ряд значений ΔV/Δr и построить дифференциальную кривую распределения объема пор по радиусам в координатах ΔV/Δr = f(r) (кривая 2).
 327. Для полного обессоливания методом ионообменной адсорбции V м3 природной или разбавленной сточной воды последовательно пропускают через колонки, содержащие m1 кг катионита в Н-форме, ДОЕкат моль-экв/кг и m2 кг анионита в ОН-форме, ДОЕ анио моль-экв/кг (табл). 1) Напишите уравнения ионообменных реакций, протекающих на катионите и анионите с участием ионов каждой соли. 2) Определите, в какой последовательности будут адсорбироваться ионы на катионите и анионите, расположив их в ряд по уменьшению адсорбируемости. 3) Пересчитайте концентрацию солей в водном растворе, выраженную в г/л, в молярную концентрацию эквивалентов (моль экв/л) и определите суммарную концентрацию солей в (моль экв/л). 4) Рассчитайте количество (m1 и m2, кг) катионита и анионита, достаточного для обессоливания заданного объема воды.
Решение. Уравнения ионообменных реакций имеют вид 1. MgCl2 2R-H + MgCl2= R2Mg + 2HCl на катионите; R-OH + HCl = RCl + H2O на анионите. 2.H2[ZnCl4] 2R-H + H2[ZnCl4]= R2Zn + 4HCl на катионите; R-OH + HCl = RCl + H2O на анионите. 3. H2[CoCl4] 2R-H + H2[CoCl4]= R2Co + 4HCl на катионите; R-OH + HCl = RCl + H2O на анионите. 4. AgNO3 R-H + AgNO3= RAg + HNO3 на катионите; R-OH + HNO3 = RNO3 + H2O на анионите. В соответствии с закономерностями адсорбции на катионите адсорбируется в первую очередь ион магния, затем Co, Zn и Ag,на анионите– хлорид-ион. Обмен ионов протекает в эквивалентных количествах, поэтому вначале пересчитываем концентрацию С, выраженную в г/л, в молярную концентрацию эквивалентов Сэк по формуле 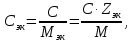 где Мэк – молярная масса эквивалентов, г/моль; Zэк – число эквивалентности, равное заряду иона по модулю. 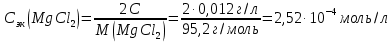 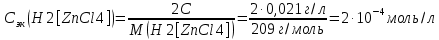 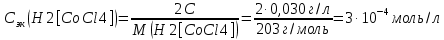 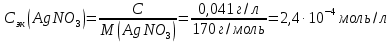 По закону эквивалентов Сэк(MgCl2) = Сэк(Mg2+) = Сэк(Cl-) Сэк( 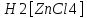 ) = Сэк(Zn2+)= Сэк(Cl-). ) = Сэк(Zn2+)= Сэк(Cl-).Сэк( 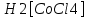 ) = Сэк(Co2+)= Сэк(Cl-). ) = Сэк(Co2+)= Сэк(Cl-).Сэк( 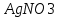 ) = Сэк(Ag+)= Сэк(NO3-). ) = Сэк(Ag+)= Сэк(NO3-).Динамическую обменную емкость ионита ДОЕ рассчитываем по формуле 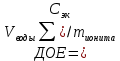 где Сэк – суммарная молярная концентрация эквивалентов всех катионитов или всех анионитов, моль/л; Vводы – объем воды, пропускаемой через ионит, л; mионита – масса катионита или анионита, кг. 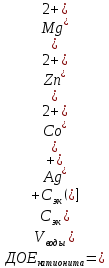 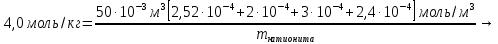 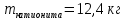 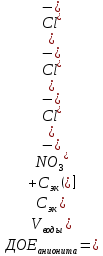 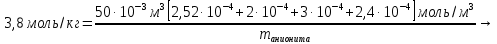 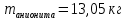 Ответ: mанионита 13,05 кг; mкатионита 12,4 кг 359. Рассчитайте электрокинетический потенциал поверхности кварца по данным, полученным при исследовании электроосмотического переноса жидкости через кварцевую мембрану: сила тока 2·10-3 А, объемная скорость раствора KCl, переносимого через мембрану, 0,02 мл/с, удельная электрическая проводимость раствора 1,2·10-2 См·м-1, вязкость раствора 1·10-3 Па·с, относительная диэлектрическая проницаемость 80,1 Дано: I=2·10-3 А η = 1·10-3 Па·с = 1·10-3 Н·с/м2 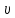 = 0,02 мл/с = 2⸱10-8 м3/с = 0,02 мл/с = 2⸱10-8 м3/сε = 80,1 k = 1,2·10-2 См·м-1 Решение: Расчет электрокинетического потенциала при электроосмосе ведут по уравнению: 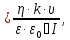 где: - величина электрокинетического потенциала, В; - вязкость среды, Н·с/м2; - диэлектрическая проницаемость среды, для водной среды равная 81 (безразмерная величина); 0 - электрическая константа (диэлектрическая проницаемость вакуума), равная 8,85·10-12 Ф/м; – удельная электрическая проводимость, Ом-1 м -1; – объемная скорость электроосмоса, м 3/с, I – сила тока, А. 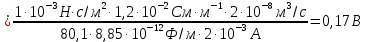 Ответ: электрокинетический потенциал поверхности кварца составил 0,17 В 367. Сточные воды производства фотоматериалов содержат коллоидное серебро в виде иодида серебра. Рассчитайте расход Al2(SO4)3, кг, на очистку 1000 м3 сточных вод, предполагая, что знак электрических зарядов коллоидных частиц положительный. Пороги коагуляции, моль/м3, для одновалентных ионов − 140; для двухвалентных – 1,98; для трехвалентных – 0,052. Решение: 1) Если электрический заряд коллоидных частиц положительный, ионами–коагуляторами являются ионы 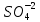 (z = 2). Порог коагуляции сточных вод по Al2(SO4)3, рассчитываем следующим образом (z = 2). Порог коагуляции сточных вод по Al2(SO4)3, рассчитываем следующим образом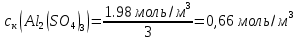 2. Рассчитаем массу (кг) Al2(SO4)3, которая необходима для коагуляции 1000 м3 сточных вод: m Al2(SO4)3= Cк(Al2(SO4)3 VB M Al2(SO4)3= 0,66 1000 0.342 = 225.7 кг. Ответ: Рассчитайте расход Al2(SO4)3, кг, на очистку 1000 м3 сточных вод составляет 225,7 кг |