методы оценки несущей способности. 3. Методы оценки несущей способности

• Название: 3. Методы оценки несущей способности
• Анкор: методы оценки несущей способности
• Дата: 21.07.2020
• Размер: 257.14 Kb.
• Имя файла: методы оценки несущей способности.docx
• Тип: Документы; #134622

3. Методы оценки несущей способности

В практике расчетов на прочность принято использовать два метода оценки несущей способности конструкции: метод допускаемых напряжений и метод разрушающих нагрузок.

Начнем с метода допускаемых напряжений, который широко используется в общем машиностроении, где требование минимальной массы играет второстепенную роль по сравнению с требованием безопасной и долговечной работы конструкции.

Допускаемые напряжения составляют долю от предела пропорциональности σ _y или предела текучести σ _0.2 , которые считаются предельными (опасными) напряжениями, т.е. [σ] = σ_0.2 /η, где η – коэффициент запаса прочности для различных конструкций η =1,5…5. На выбор требуемого коэффициента запаса прочности влияют следующие факторы:

1) степень точности определения действующих нагрузок и применяемых методов расчета;

2) степень однородности используемых материалов конструкции, их чувствительность к механической обработке и уровень разброса физико-механических свойств;

3) ответственность детали.

Обычно коэффициент запаса прочности представляется в виде произведения частных коэффициентов запаса, учитывающих влияние различных факторов на надежность работы проектируемой конструкции.

Таким образом, при использовании метода допускаемых напряжений конструкция всегда работает в пределах упругих деформаций, причем расчетные напряжения меньше допускаемых, т.е. σ_р ≤ [σ].

Так как пластические деформации в конструкции отсутствуют, то в этом методе коэффициенты запаса прочности по нагрузкам и напряжениям будут одинаковыми. Как следует из диаграммы растяжения стального образца, приведенной на рис. 4, это совпадение будет соблюдаться на линейном участке кривой, вплоть до предела пропорциональности σ _y .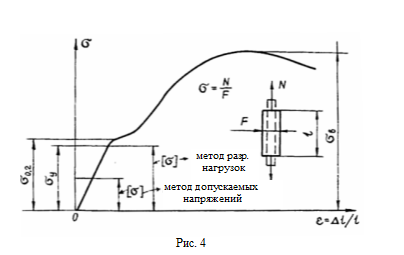



За пределом пропорциональности происходит перераспределение напряжений и пропорциональность между напряжениями и нагрузкой нарушается. Это означает, что на участке работы конструкции с пластическими деформациями запас прочности по напряжениям не позволяет судить о запасе прочности по ее нагрузкам. При проектировании ракет фактор массы играет решающую роль, поэтому конструкция проектируется так, чтобы прочностные свойства материала использовались полностью. Поэтому в качестве допускаемых напряжений в ракетостроении принимают предел пропорциональности или предел текучести (если остаточные деформации допустимы), а не часть их, как в общем машиностроении.

Запасы прочности в этом случае перекрывают область, где коэффициенты запаса по напряжениям и нагрузкам будут различными, и поэтому расчет конструкции ведется по разрушающим нагрузкам, которые в наибольшей степени характеризуют ее работоспособность.

Коэффициент запаса прочности в методе разрушающих нагрузок равен: η = N _разр /[N ], где [N] – допускаемая нагрузка, т.е., обеспечивающая возникновение безопасных напряжений (в данном случае предела пропорциональности).

Если ввести понятие расчетной нагрузки N _р , под которой следует понимать нагрузку, действующую на конструкцию, то метод допускаемых напряжений метод разр. нагрузок N _р ≤ [N ] = N _разр / η . Однако установить разрушающую нагрузку N _разр расчетным путем, за исключением простейших случаев, не представляется возможным, поэтому в методе разрушающих нагрузок поступают следующим образом.

Принимают коэффициент запаса прочности η равным единице, а требуемый запас вводят в расчетную нагрузку, которая теперь умножается на коэффициент безопасности f. Для того чтобы различать завышенную таким образом расчетную нагрузку и нагрузку, действующую на конструкцию, последнюю называют эксплуатационной N _э , т.е. теперь N _р = fN _э . Эта нагрузка и используется при расчете конструкции на прочность в методе разрушающих нагрузок. Что касается коэффициента запаса прочности, то в общем случае его можно определить экспериментальным путем после вычисления N _разр . Теперь η = N _разр / N _р ≈1 (не менее 0,98), и роль его сводится к оценке степени совершенства спроектированной конструкции.

Значение коэффициента безопасности установить теоретически довольно трудно, так как невозможно выявить все факторы, влияющие на его величину. В основном роль коэффициента безопасности сводится к компенсации:

1) несоответствия между детерминистским расчетным и фактическим случайным представлением внешних нагрузок, внутренних усилий и несущей способности конструкции;

2) отклонения расчетной схемы ЛА и расчетных условий его нагружения от действительных.

Это заставляет набирать статистические данные по коэффициентам безопасности, чтобы использовать их в дальнейшем для проектирования новых конструкций.

31. Скоростной напор на траектории БР

Полную аэродинамическую нагрузку, отнесенную к единице площади, в каждой точке корпуса можно разложить на касательную к поверхности (т) и нормальную (Др_и) составляющие (рис. 19). В свою очередь, касательную проекцию в общем случае можно разложить на составляющие, направленные по касательной к меридиану и параллели. Последней, ввиду ее малости, обычно пренебрегают. Нормальная составляющая есть не что иное, как давление. Она-то и представляет наибольший интерес в расчетах на прочность. Полное давление, действующее на корпус ракеты в данной точке, равно: р = р_н+ Ар_а, где р_п - давление воздуха на высоте Я; Ар_а - избыточное давление воздуха, возникающее вследствие взаимодействия его с ракетой.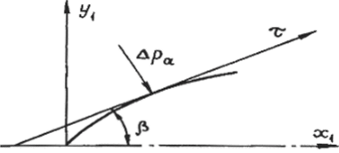



Рис. 19

При вычислении аэродинамических нагрузок учитывается лишь вторая составляющая давления, т.е. Ар_а , гак как первая учтена в формуле для тяги, которая определяется как интеграл от сил давления по внутреннему и внешнему контуру ракеты в проекции на ее ось симметрии. Причем под внешним давлением понимается давление в окружающей среде.

Исходными для расчета аэродинамических нагрузок являются графики распределения давления Ар_а и сил трения т на единицу площади по корпусу ракеты.

Получим аналитические выражения для расчета аэродинамических нагрузок по известным исходным данным.

Сила лобового сопротивления и подъемная сила всей ракеты равны: Х_х = c_x]qS_m, = c_y]aqS_m, где q - скоростной напор. Здесь

следует отметить важную особенность графика скоростного напора в зависимости от времени, которая состоит в том, что на активном участке траектории и на участке входа в плотные слои атмосферы этот график имеет максимум (рис. 20).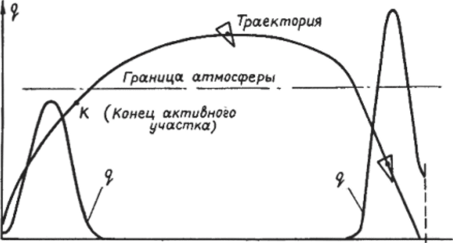



Рис. 20

На основании статистических данных, полученных для баллистических ракет, установлено, что на активном участке (рис. 21) <="" i="">< 0,5, где Т = т₀ /т - время, за которое сгорела бы вся стартовая масса ракеты. Указанный диапазон I =t/T соответствует числам Маха в области 2,5>М>1,5. Значение максимального скоростного напора существенно зависит от удельной тяги двигателя и стартовой перегрузки. Для определения максимальной силы лобового сопротивления можно воспользоваться зависимостью, полученной в результате обработки статистических данных:  где к_х, р, v - статистические коэффициенты; У, - удельная тяга двигателя; и₀ = Т_(} ) - стартовая перегрузка. Для одноступенчатых ракете параметрами п₀=1,5ч-2, ./, =(2000 ч- 2600) Нс/кг

можно принимать к_х =4-10⁴ Н/м², р = 1,0» v = 0,25. В других случаях структура зависимости останется прежней, а статистические коэффициенты к_х,$, v могут быть приняты на основе ближайшего прототипа проектируемой ракеты.



Рис. 21

Для расчета максимального скоростного напора на активном участке траектории БР можно воспользоваться также следующими соотношениями

Скорость полета (м/с):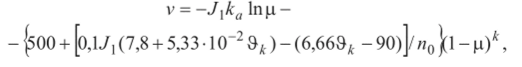



где 1 = т/т₀ - относительная масса ракеты (т, т₀ - текущее и стартовое значения массы),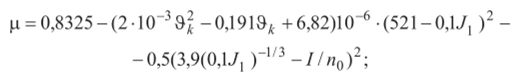



п₀ - начальная тяговооруженность ступени; - удельная тяга двигателя на Земле; к_а =(1,05 ч-1,15) - коэффициент увеличения удельной тяги в пустоте; 9* - угол наклона вектора скорости к плоскости горизонта в конце активного участка, в градусах.

Высота (км), на которой достигается максимальный скоростной напор, равна: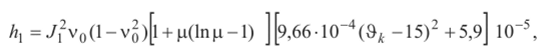



где v₀ = 1/я₀ - стартовая нагрузка на тягу.

Плотность воздуха р = 1,225 ехр(-А, /6,3).

Для определения числа Маха, которое требуется при расчете аэродинамических коэффициентов, сначала находят температуру воздуха на высоте А, км. В соответствии с рекомендациями [5] атмосферный участок траектории в диапазоне высот 0 < А < 85 делится на участки, в пределах которых температура аппроксимируется линейной функцией вида Т = Т, + Ь(1ц - А), где индекс « относится к нижней границе рассматриваемого слоя, а значения коэффициента А и температур на границах слоев берутся из табл. 4.1. Тогда скорость звука (м/с) а =20,04 л/т, а число Маха на высоте А] М = v/a.

Таблица 4.1

Параметры	Высота, км
	0	11,1	20	32	47	51	71	85
ь	-Д510'	0	105	22110'	0	-2,810J	-210Г3	-
Т.	286,15	216,65	216,68	228,65	270,65	270.65	214,65	186,65

Конечно, при проверочных расчетах на прочность значение Х_тах может быть определено по данным траекторных расчетов ракеты. Выражения для элементарных аэродинамических сил, действующих на кольцевой участок корпуса длиной dx_t, изображенный на рис. 22, запишем в виде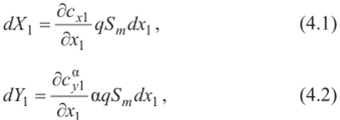



где с_х| = с_х| (а, М, х,), с“, = с", (а, М, х,).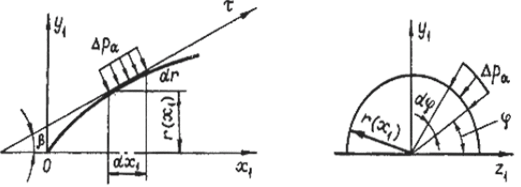



Рис. 22

С другой стороны, на основании данных о распределении давления и трения по корпусу эти же силы равны: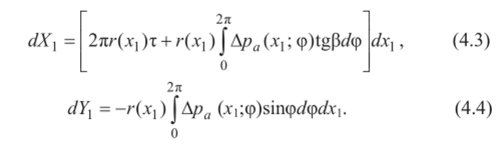



В (4.4) отброшена поперечная составляющая, создаваемая силами трения, ввиду ее малости по сравнению с составляющей, создаваемой силами давления. Приравнивая (4.1) и (4.3), (4.2) и (4.4), получаем



Таким образом, производные от аэродинамических коэффициентов, могут быть вычислены в каждом поперечном сечении ракеты по известному распределению Др_а и т .

Очевидно, эти производные зависят от координаты х, что иллюстрирует график одной из производных, построенный на рис. 23 для ракеты «Европа-1».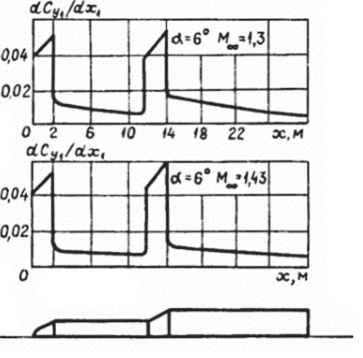



Рис. 23

По известным производным от аэродинамических коэффициентов нетрудно определить и соответствующие аэродинамические нагрузки в сечении, расположенном на расстоянии хi от носка ракеты. Осевая аэродинамическая нагрузка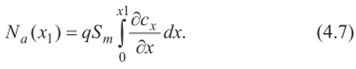



Перерезывающая сила и изгибающий момент: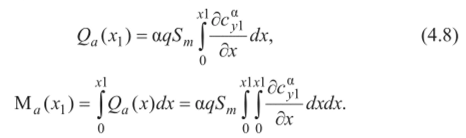



Если аэродинамические нагрузки определяются на 1раницах участков, на которые разбит корпус по длине, то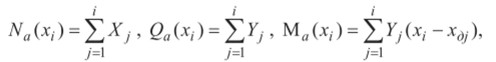 

где Xj, Yj - сила лобового сопротивления (без донной составляющей) и подъемная сила у-го участка; х, - координата правой границы рассматриваемого участка; x_dj - координата центра давления у'-го участка, измеряемая от носка ракеты.

Из приведенных зависимостей видно, что максимальное значение осевых аэродинамических нагрузок на активном участке достигается при максимальном скоростном напоре. Полная сила лобового сопротивления всей ракеты отличается от осевой аэродинамической нагрузки у основания ракеты N_a(I) на величину силы донного сопротивления, и поэтому X_t = N_a(l) + X_д. Если подставить (4.5) и (4.6) для производных от аэродинамических коэффициентов в (4.7) и (4.8), то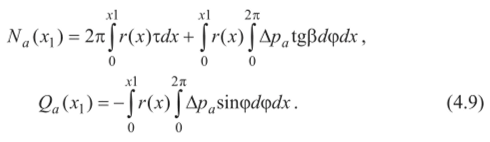



Следует заметить, что определение Ар_а и т в общем случае представляет самостоятельную аэродинамическую задачу, которая в настоящее время часто решается экспериментально, и лишь в отдельных простейших случаях можно получить аналитические зависимости или численные решения.