Математическое моделирование в прочностных расчетах
 Скачать 317.06 Kb. Скачать 317.06 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых» (ВлГУ) Кафедра сопротивления материалов Практическая работа по математическому моделированию Тема: Математическое моделирование в прочностных расчетах элементов строительных конструкций
Задача №1 Данные (шифр 4602):
Расчетное сопротивление R = 200 МПа. Решение: 1. Составляем расчетную схему балки, указав заданные размеры и нагрузку (рисунок 1). 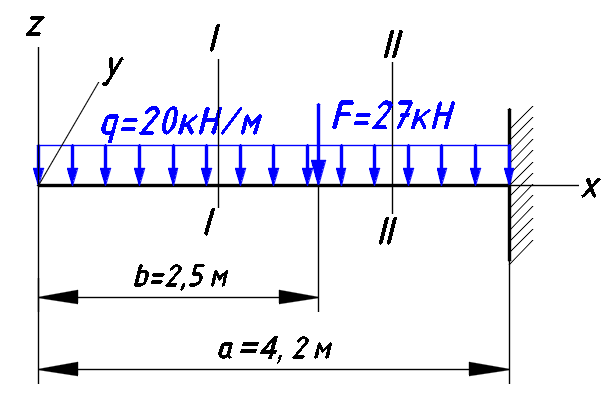 Рисунок 1 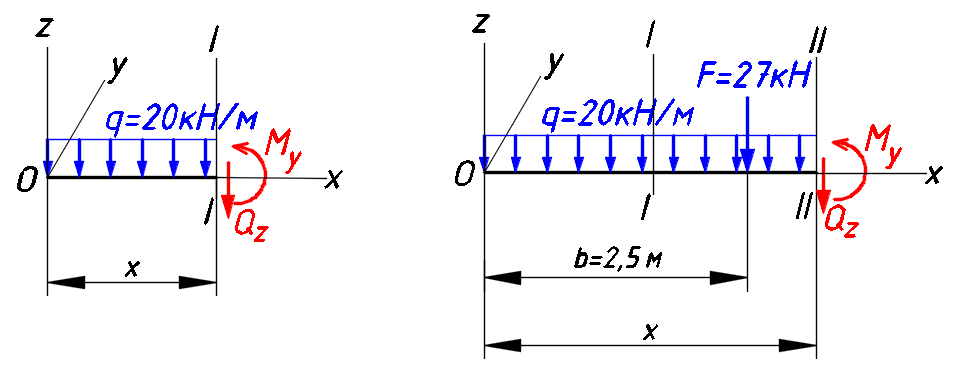 Рисунок 2 Рисунок 3 2. Для определения внутренних усилий и построения эпюр используем метод сечений. На балке два участка, начнем рассматривать со свободного конца. Продольную ось х, поперечные оси у и z направим, как показано на расчетной схеме. Проведем сечение I-I на 1-ом участке и рассмотрим равновесие левой отсеченной части. Покажем в сечении положительные направления поперечной силы Qz и изгибающего момента Мy(рисунок 2). Составим уравнения равновесия, из которых найдем внутренние усилия: Сечение I-I: 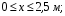 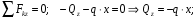 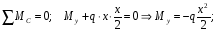 Подсчитываем значения внутренних усилий на границах 1-го участка: 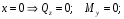 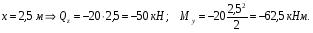 Проведем сечение II-II на 2-ом участке и рассмотрим равновесие левой отсеченной части. Покажем в сечении положительные направления поперечной силы Qz и изгибающего момента Мy(рисунок 3). Составим уравнения равновесия, из которых найдем внутренние усилия: Сечение II-II: 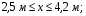 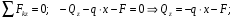 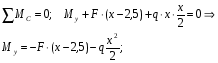 Подсчитываем значения внутренних усилий на границах 2-го участка: 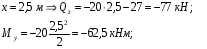 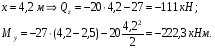 Строим эпюры поперечных сил и изгибающих моментов (рисунок 4). При этом учтем, что знак поперечной силы на участках не меняется, т.е. изгибающий момент не имеет экстремума на участках. Опасное сечение находится в заделке, где изгибающий момент имеет максимальное по модулю значение. 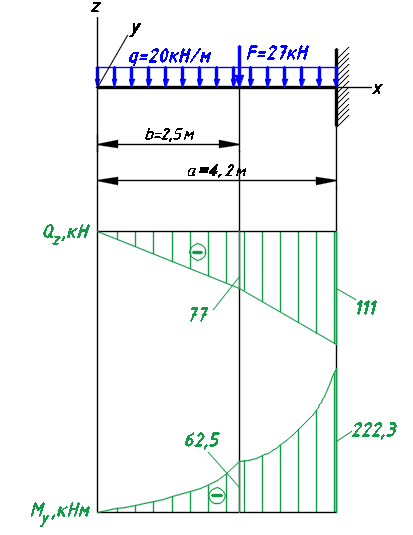 Рисунок 4 3. Запишем условие прочности при изгибе по нормальным напряжениям: 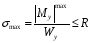 . .4. Определим из условия прочности осевой момент сопротивления поперечного сечения: 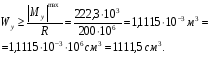 5. Определим размеры поперечного сечения балки для заданных форм (рисунок 5). 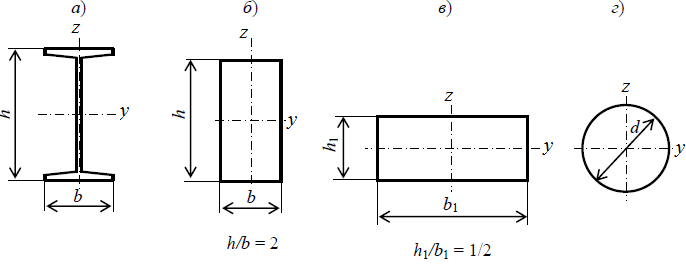 Рисунок 5 а) подбираем по таблице сортамента (ГОСТ 8239-89) двутавр №45, для которого осевой момент сопротивления Wy= 1231 см3 (мы учли, что в нашем случае ось у направлена как ось х в сортаменте, т.е. из таблицы взято значение Wх ). б) для прямоугольника 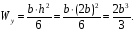 Отсюда 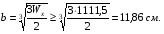 Примем b=12 см, тогда h=24 см. в) для прямоугольника 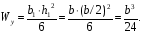 Отсюда 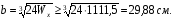 Примем b1=30 см, тогда h1=15 см. г) для круглого сечения 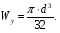 Отсюда 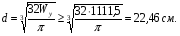 Примем d=23 см. 6. Проведем сравнение балок с указанными формами поперечного сечения по расходу материала (по весу). Так как длины балок одинаковы, то вес балки пропорционален площади поперечного сечения. Из ГОСТа 8239-89 находим площадь поперечного сечения двутавра №45, она равна А=84,7 см2. Площадь прямоугольного поперечного сечения балки со сторонами bиh равна А=b∙h=12∙24=288 см2. Площадь прямоугольного поперечного сечения балки со сторонами b1иh1 равна А=b1∙h1=30∙15=450 см2. Площадь круглого поперечного сечения балки равна 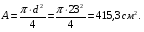 . . Как видно из сравнения, минимальная площадь у двутаврового поперечного сечения, поэтому оно является самым экономичным. Таким образом, выбираем самое рациональное сечение по расходу материала – двутавр №45. Ответ: двутавр №45. Задача №2 Данные (шифр 4602):
Расчетные сопротивления: при сжатии Rсж=140 МПа, при растяжении Rраст=50 МПа. Решение: 1. Составляем расчетную схему балки, указав заданные размеры и нагрузку (рисунок 6). 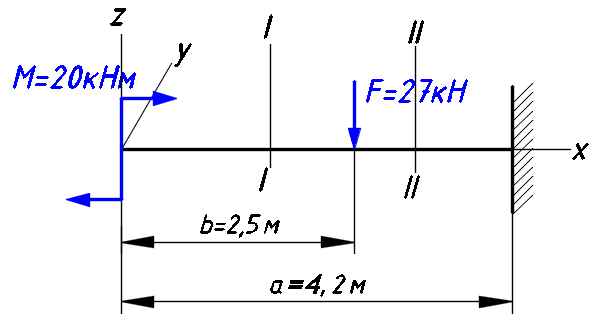 Рисунок 6 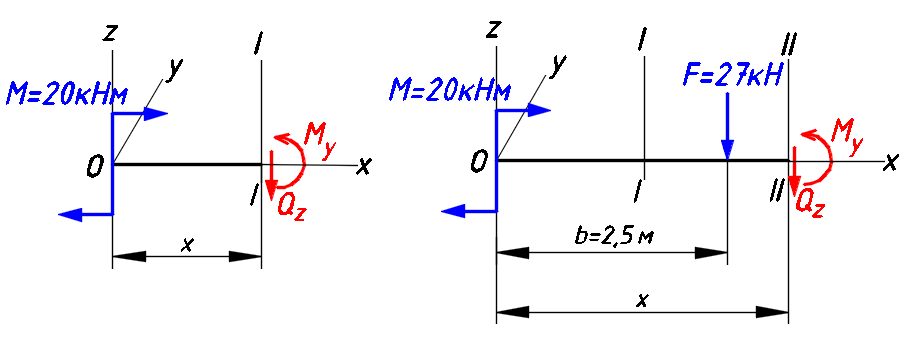 Рисунок 7 Рисунок 8 2. Для определения внутренних усилий и построения эпюр используем метод сечений. На балке два участка, начнем рассматривать со свободного конца. Продольную ось х, поперечные оси у и z направим, как показано на расчетной схеме. Проведем сечение I-I на 1-ом участке и рассмотрим равновесие левой отсеченной части. Покажем в сечении положительные направления поперечной силы Qz и изгибающего момента Мy(рисунок 7). Составим уравнения равновесия, из которых найдем внутренние усилия: Сечение I-I: 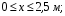 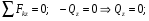 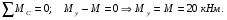 Проведем сечение II-II на 2-ом участке и рассмотрим равновесие левой отсеченной части (рисунок 8). Составим уравнения равновесия, из которых найдем внутренние усилия: Сечение II-II: 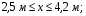 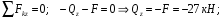 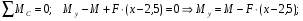 Поперечная сила постоянна на участке, подсчитываем значения изгибающего момента на границах 2-го участка: 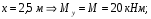 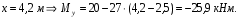 Строим эпюры поперечных сил и изгибающих моментов (рисунок 9). Опасное сечение находится в заделке, где изгибающий момент имеет максимальное по модулю значение. 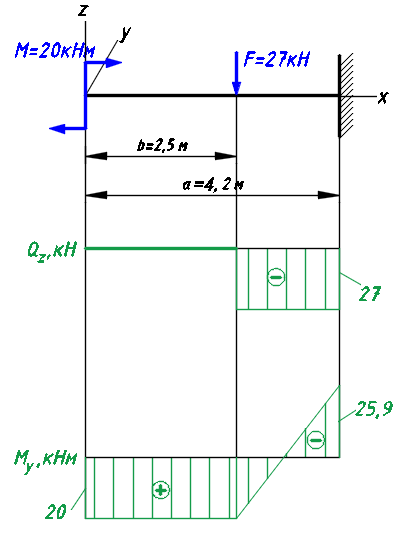 Рисунок 9 3. Так как материал балки неодинаково сопротивляется растяжению и сжатию, то условие прочности запишется отдельно для растягивающихся и сжимающихся волокон: 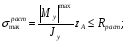 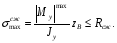 Здесь точки А и В наиболее удаленные от нейтральной оси точки. Для определения их расстояний zA, zB от нейтральной оси и осевого момента инерции Jy необходимо вначале найти центр тяжести сечения. Для этого разобьем сечение на два прямоугольника (рисунок 10,а) и определим координату центра тяжести по формуле: 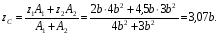 Покажем центр тяжести сечения и укажем расстояния от него до центров тяжести прямоугольников (рисунок 10,б). 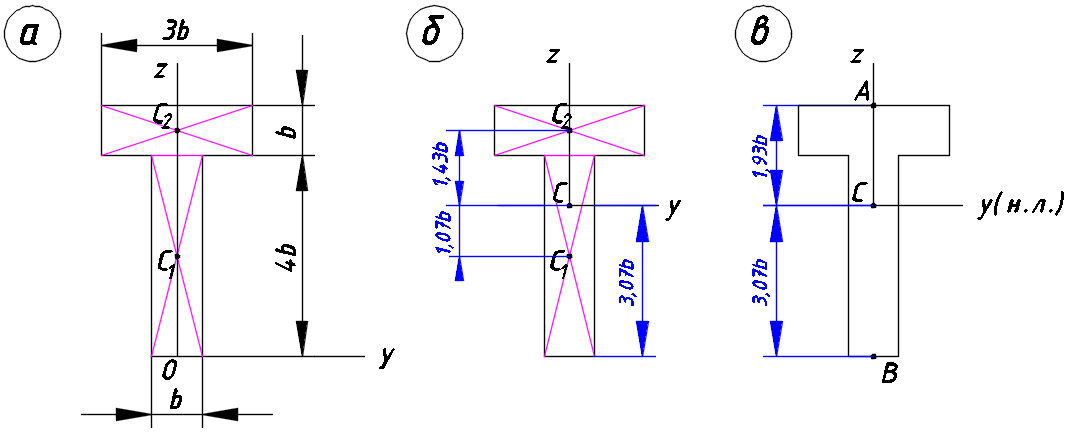 Рисунок 10 Нейтральная ось проходит через центр тяжести сечения (ось у). Определяем момент инерции поперечного сечения относительно нейтральной оси, как сумму осевых моментов инерции двух прямоугольников: 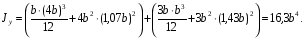 4. Определим размеры поперечного сечения. В сечении, где изгибающий момент имеет наибольшее по модулю значение, верхние волокна испытывают растяжение, поэтому балку следует расположить полкой вверх (рисунок 10,в). Определяем размер b из расчета на прочность по наибольшим растягивающим напряжениям в этом сечении: 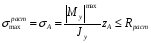 или или 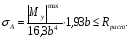 Отсюда 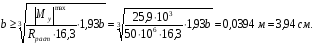 Примем b=4 см. 5. Проверим выполнение условия прочности по сжимающим напряжениям в сечении, где изгибающий момент имеет наибольшее по модулю значение (в заделке): 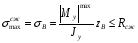 . .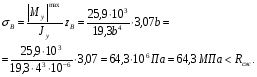 Как видно, наибольшие сжимающие напряжения в этом сечении значительно ниже расчетного. Необходимо также проверить прочность по наибольшим растягивающим напряжениям в сечениях на 1-ом участке, так как хотя там момент и меньше максимального, но сечение балки расположено нерационально – растянуты нижние волокна. Опасной является точка В, в которой возникают наибольшие растягивающие напряжения: 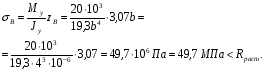 Условие прочности выполнено. Ответ: b=4 см. Задача №3. Данные (шифр 4602):
Расчетное сопротивление растяжении и сжатии R = 210 МПа, при срезе R = 120 МПа. Решение: 1. Составляем расчетную схему балки, указав заданные размеры и нагрузку, а также реакции опор балки (рисунок 11). 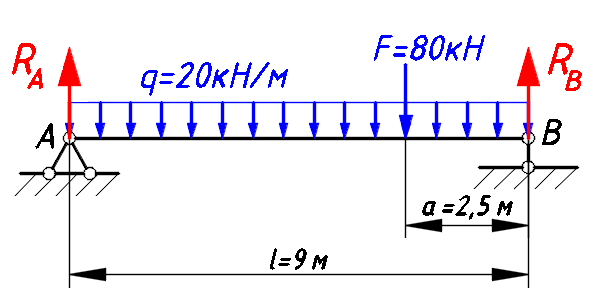 Рисунок 11 Найдем реакции опор балки из уравнений равновесия: 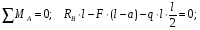 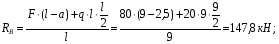 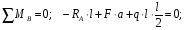 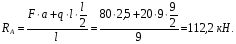 Выполним проверку правильности определения реакций опор, составив уравнений проекций сил на вертикальную ось: 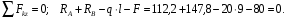 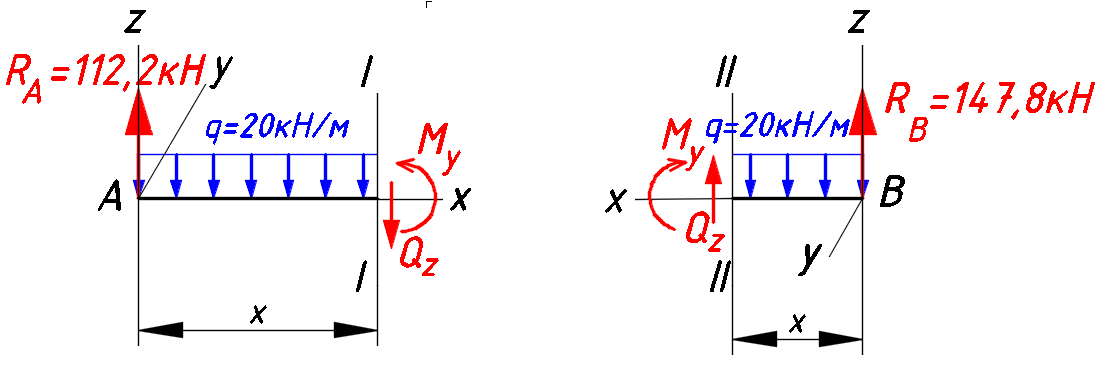 Рисунок 12 Рисунок 13 Для определения внутренних усилий и построения эпюр используем метод сечений. Проведем сечение I-I на 1-ом участке и рассмотрим равновесие левой отсеченной части(рисунок 12). Составим уравнения равновесия, из которых найдем внутренние усилия: Сечение I-I: 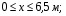 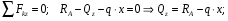 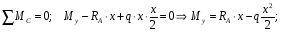 Подсчитываем значения внутренних усилий на границах 1-го участка: 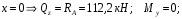 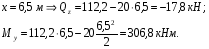 Так как поперечная сила Qzменяет знак на 1-м участке, то изгибающий момент имеет экстремум в сечении, где Qz= 0. Найдем координату этого сечения: 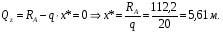 Найдем значение изгибающего момента в этом сечении: 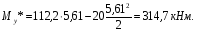 Проведем сечение II-II на 2-ом участке и рассмотрим равновесие правой отсеченной части(рисунок 13). Составим уравнения равновесия, из которых найдем внутренние усилия: Сечение II-II: 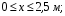 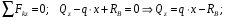 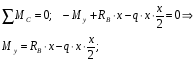 Подсчитываем значения внутренних усилий на границах 2-го участка: 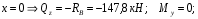 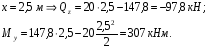 Так как знак поперечной силы на 2-ом участке не меняет знак, то изгибающий момент на этом участке не имеет экстремума. Строим эпюры поперечных сил и изгибающих моментов (рисунок 14). На эпюре поперечной силы в сечениях, где приложены сосредоточенные силы есть скачки, равные по величине эти силам. На эпюре изгибающих моментов скачков нет, так как нет приложенных к балке сосредоточенных моментов. Опасное сечение находится в сечении, где изгибающий момент имеет максимальное по модулю значение. 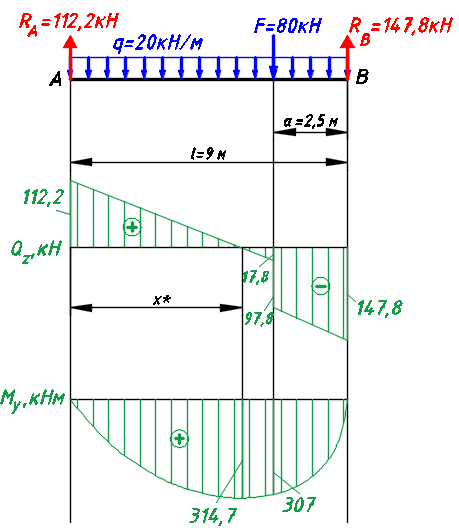 Рисунок 14 3. Запишем условие прочности при изгибе по нормальным напряжениям: 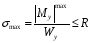 . .4. Определим из условия прочности осевой момент сопротивления поперечного сечения: 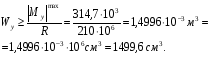 Подбираем по таблице сортамента (ГОСТ 8239-89) двутавр №50, для которого осевой момент сопротивления Wy= 1589 см3 (мы учли, что в нашем случае ось у направлена как ось х в сортаменте, т.е. из таблицы взято значение Wх ). Тогда максимальное нормальное напряжение 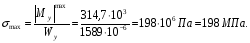 5. Проведем уточнение модели балки, учтя ее вес. Для двутавра №50 находим в таблице сортамента массу 1 метра: m=66,5 кг/м. Тогда вес одного метра при g=10 м/с2 равен q′=665 Н/м=0,665 кН/м. Таким образом, вес балки учтем как дополнительную равномерно распределенную нагрузку интенсивностью q′. Тогда в выражениях для реакций опор и внутренних усилий необходимо принять вместо значения q значение qобщ=q+q′=20,665 кН/м. Найдем реакции опор балки: 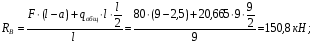 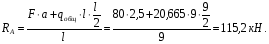 Проверка: 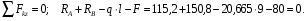 Тогда координата опасного сечения, где изгибающий момент имеет наибольшее значение: 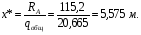 Найдем значение изгибающего момента в этом сечении: 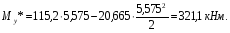 Вычислим максимальное нормальное напряжение в опасном сечении: 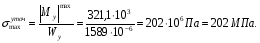 6. Определим в процентах отклонение максимального нормального напряжения для уточненной модели балки с учетом ее веса от максимального нормального напряжения для модели балки без учета ее веса: 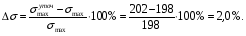 Как видно, разница в максимальных нормальных напряжениях мала, поэтому расчет балки на прочность можно проводить по первоначальной модели балки без учета ее веса. 7. Определим наибольшее касательное напряжение в сечении, где поперечная сила имеет максимальное по модулю значение (в сечении над опорой В). Максимальное касательное напряжение имеет место на нейтральной оси этого сечения (т.е. на оси у) и определяется по формуле: 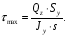 Для двутавра №50 из таблицы сортамента находим (с учетом направления осей): статический момент половины сечения относительно нейтральной оси Sy=919 см3, осевой момент инерции поперечного сеченияJy=39727 см4, толщина сечения на нейтральной оси (толщина стенки) s=10 мм. Подсчитаем наибольшее касательное напряжение и сравним его с расчетным напряжением при срезе R=120 МПа: 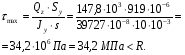 Таким образом условие прочности по касательным напряжениям выполнено. Ответ: двутавр №50. Владимир 2019г. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
