Сопромат эпюры. 3443584 эпюры внутренних усилий. Дано f 1 25 кН, F
 Скачать 337.57 Kb. Скачать 337.57 Kb.
|
|
Для заданных стержня, вала, балки определить: опорные реакции построить эпюры внутренних силовых факторов Дано: F1=25 кН, F2=30 кН, q=12 кН/м, а=1,5м 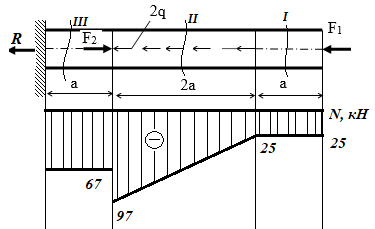 Решение: 1.Определяем опорную реакцию 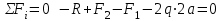 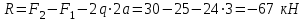 2. Определение продольных сил Продольные силы, возникающие в поперечных сечениях стержня, будем определять с помощью метода сечения. Участок I 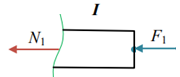 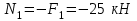 Участок II 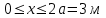 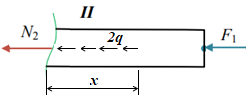 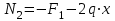 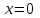 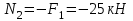 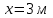 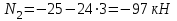 Участок III 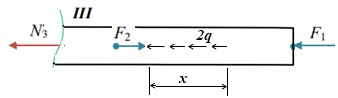 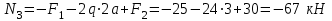 По полученным данным строим эпюру, показывающую изменение продольной силы N по длине стержня. Дано: m1=70 кН·м, m2=45 кН·м, m3=30 кН·м, а=1,5м 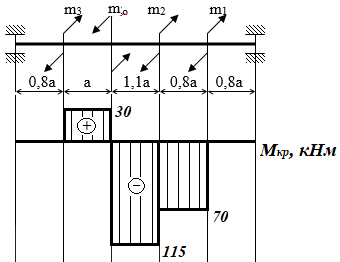 Решение: Определяем уравновешивающий момент m0 из условия равновесия вала. SМz = 0; М 1 + М 2 + М 3 – M0 =0;М 0 = М 1 + М2 + M3= 70 + 45+30= 145 кН·м.Разбиваем вал на участки - границами участков являются сечения, в которых приложены внешние вращающие моменты. В данном примере вал имеет 3 участкa. Участок I 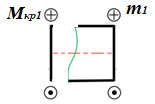 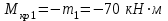 Участок II 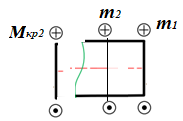  Участок III 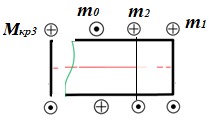 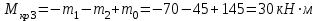 По полученным данным строим эпюру крутящего момента МКР по длине стержня. Дано: F1=25 кН, q=12 кН/м, а=1,5м 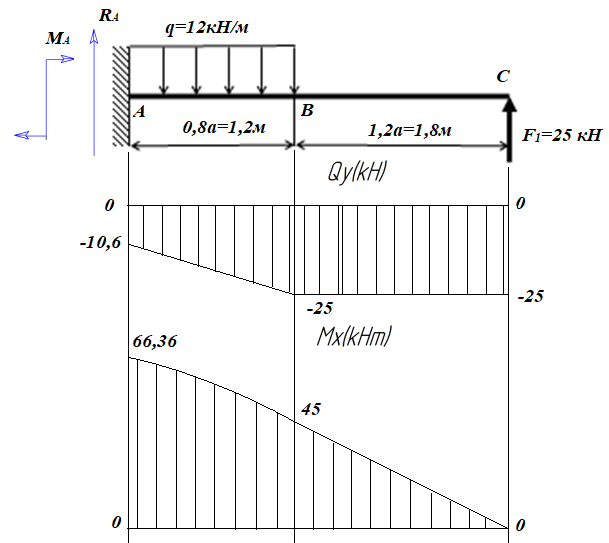 Решение: В заделке А балки, нагруженной внешними нагрузками, возникает реактивный изгибающий момент MА и реактивная сила R (составляющие RAY и RAX=0). Составим уравнения равновесия 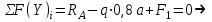 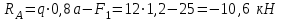 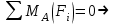 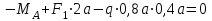 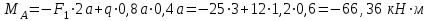 Разобьем балку на участки и рассмотрим каждый в отдельности. Первый участок.0≤ u1≤ 1,8м  Qу1 = -F=-25 кН - уравнение прямой параллельной нулевой линии.
Mx1=F1·u1- уравнение прямой линии
Второй участок.0≤ u2≤ 1,2м  Qу1 = – F+q∙u2= –25+12u2 – уравнение прямой.
Mx1= F∙(1,8+u2) – qu2∙u2/2= F∙(1,8+u2) – q∙u12 /2 Mx1 = 45+25·u2 – 6∙u12 - уравнение параболы Исследуем уравнение на экстремум: Mx1'= -12∙u2+ 25 -12·u2+25=0 u2=2,083м (Не входит в пределы второго участка) (Точка максимума) Mх2''= -12 => ветви параболы направлены вниз
По решению аналитических выражений на всех участках, получаем, что при действии на балку внешних силовых факторов, в её поперечном сечении возникают два внутренних силовых фактора Qу и Mx. Построим эпюры внутренних силовых факторов Qу и Mx. Дано: М=10 кНм, q=12 кН/м, а=1,5м 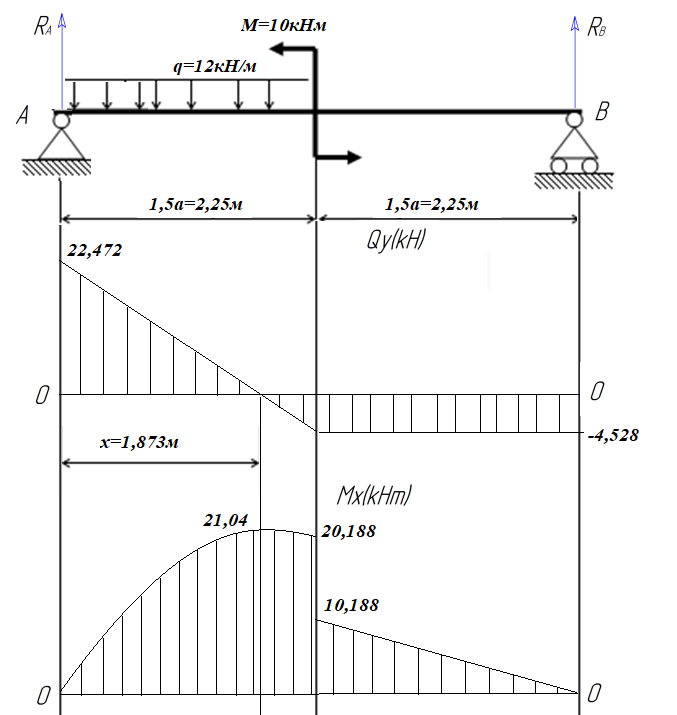 Решение: Расставим и определим все опорные реакции. Для этого необходимо составить и решить два уравнения статики: ΣmomAFi=0 RB·3a+M-q·1,5a·0,75a=0 RВ= (-M+1,125qа2 )/3а= (-10+1,125·12·1,52 )/3·1,5 =4,528 (кН) ΣmomВFi=0 -RА·3a+M+q·1,5a·(0,75a+1,5а)=0 RА=( M+q·1,5a·(0,75a+1,5а))/3а=( 10+12·2,25·(1,125+2,25))/4,5 =22,472 (кН) Проверка: ΣпруFi=0 RA+ RВ-q×2,25=0 22,472+4,528-12·2,25=0 Разобьем балку на участки и рассмотрим каждый в отдельности. Первый участок.0≤ u1≤ 2,25м  Qу1 =RA - q∙u1 =22,472-12·u1 - уравнение прямой.
Mx1=RA∙u1 -qu1∙u1/2= -q∙u12 /2 +RA∙u1 Mx1 =-6∙u12 + 22,472∙u1 - уравнение параболы Исследуем уравнение на экстремум: Mx1'= -12∙u1+ 22,472 -12∙u1+ 22,472=0 u1=1,873 м( Входит в пределы первого участка) (Точка максимума) Mх1''= -12 => ветви параболы направлены вниз
Второй участок.0≤ u2≤ 2,25м  Qу2 = -RB=-4,528 кН - уравнение прямой параллельной нулевой линии.
Mx2=RB·u2- уравнение прямой линии
По решению аналитических выражений на всех участках, получаем, что при действии на балку внешних силовых факторов, в её поперечном сечении возникают два внутренних силовых фактора Qу и Mx. Построим эпюры внутренних силовых факторов Qу и Mx. Дано: q=12 кН/м, а=1,5м 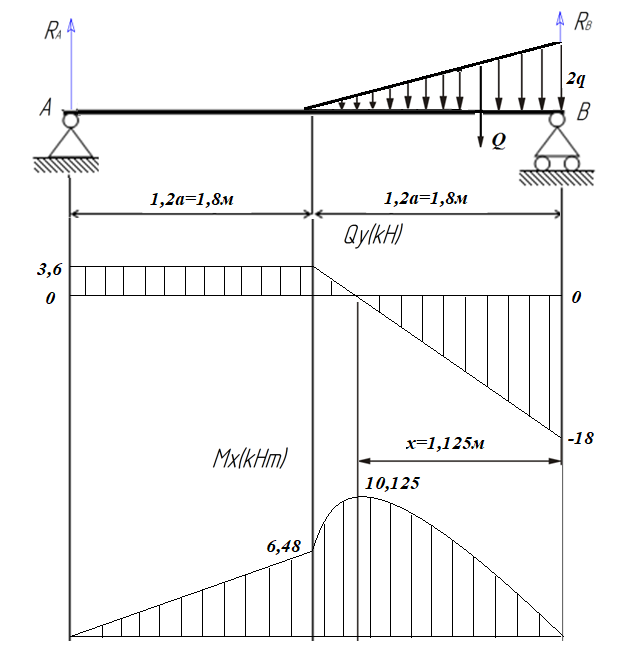 Решение: Расставим и определим все опорные реакции. Заменим участок с неравномерно распределенной нагрузкой длиной 1,8м равнодействующими, приложенными в центрах тяжести треугольников 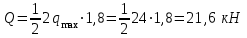 Составим и решим два уравнения статики: 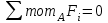 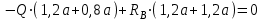 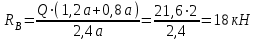 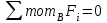 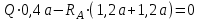 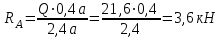 Проверка: 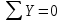 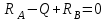 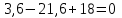 2)Разобьем балку на участки и рассмотрим каждый в отдельности. Первый участок.0≤ u1≤ 1,8м 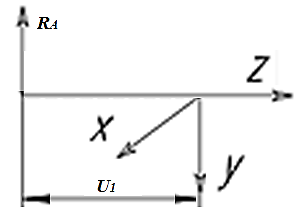 Qу1 = RA=3,6кН - уравнение прямой параллельной нулевой линии.
Mx1=RA·u1= 3,6·u1- уравнение прямой линии
Второй участок.0≤ u2≤ 1,8м 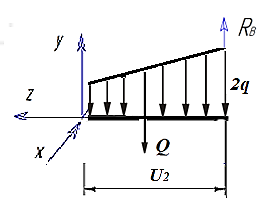 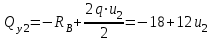 - уравнение прямой линии - уравнение прямой линии
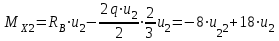 - уравнение параболы - уравнение параболыИсследуем уравнение на экстремум: Mx2'= -16∙u2+ 18 -16∙u2+ 18=0 U2=1,125 м( Входит в пределы первого участка) (Точка максимума) Mх2'= -16 => ветви параболы направлены вниз
|
