Задачи. 3 вариант. Задачи

• Название: 3 вариант. Задачи
• Дата: 08.12.2018
• Размер: 24.72 Kb.
• Имя файла: Задачи.docx
• Тип: Документы; #59312

3 вариант. Задачи:

3. Стоимость портфеля инвестора составляет 5 млн. руб., VaR для одного дня с доверительной вероятностью 95% равен 60 тыс. руб. В течение какого количества дней из каждых 100 дней инвестор вправе ожидать, что его потери не превысят 60 тыс. руб.

Решение:

Стоимостная мера риска (VaR) – выраженная в денежных единицах оценка величины, которую не превысят ожидаемые в течение заданного времени убытки с данной вероятностью. 100 дней принимаются за 100%. Соответственно, 95% VaR равен 95 дням.

Ответ: 95 дней.

9. Определить однодневный VaR с доверительной вероятностью 95% для портфеля стоимостью 10 млн. руб., в который входят акции только одной компании. Стандартное отклонение доходности акции в расчете на день равно 1,5%.

Решение:

По таблице нормального распределения (функция Лапласа) находим, что уровню доверительной вероятности в 95% соответствует 1,65 стандартных отклонений. VaR портфеля равен:

VaR = 10000000 * 1,65 * 0,015 = 247500 рублей.

Ответ: однодневный VaR равен 247,5 т.р.

15. Портфель инвестора состоит из акций компаний А и В. Коэффициент корреляции между доходностями акций компаний равен +0,75. Однодневный VaR с доверительной вероятностью 95% по акциям компании А равен 40 тыс. руб., по акциям компании В — 60 тыс. руб. Определить диверсифицированный VaR портфеля из данных бумаг.

Решение:

VAR (P)=(40^2+60^2+2*0,75*40*60)^0,5=(1600+3600+1,5*2400) ^0,5 = 8800 ^ 0,5 = 93808,32 руб.

Ответ: 93808,32 руб.

21. Стоимость портфеля инвестора составляет 6 млн. руб., VaR для одного дня равен 55 тыс. руб. с доверительной вероятностью 99%. Как можно интерпретировать данную информацию?

I. Вероятность того, что в течение следующих 24 часов потери в стоимости портфеля составят меньше 55 тыс. руб. равна 99%.

II. Вероятность того, что в течение следующих 24 часов потери в стоимости портфеля превысят 55 тыс. руб. равна 1%.

III. Инвестор вправе ожидать, что в среднем его потери в течение 99 дней из каждых 100 дней окажутся больше 55 тыс. руб., или что они не превысят 55 тыс. руб. в течение 1 дня из каждых 100 дней.

Решение:

Информацию можно интерпретировать как:

I. Вероятность того, что в течение следующих 24 часов потери в стоимости портфеля составят меньше 55 тыс. руб. равна 99%.

II. Вероятность того, что в течение следующих 24 часов потери в стоимости портфеля превысят 55 тыс. руб. равна 1%.

Ответ: верные ответы I и II.

27. Курс доллара составляет 1 долл.=28 руб.. курс евро - 1евро =34 руб. Российский банк осуществил короткую продажу на спотовом рынке 500 тыс. долл. и 600 тыс. евро. Стандартное отклонение курса доллара к рублю в расчете на один день составляет 0,4%, евро к рублю - 0,55%, коэффициент корреляции между курсами долл./руб. и евро/руб. равен 0,85. Определить однодневный VaR портфеля с доверительной вероятностью 95%.

Решение:

S$=500*28=14 000 тыс.руб.

S€=600*34=20 400 тыс.руб.

θ$=14000/(14000+20400)=0,407

θ€=20400/(14000+20400)=0,593

σ = √0,407^2 × 0,4^2 +0,593^2 × 0,55^2 − 2 × 0,407 × 0,4 × 0,593 × 0,55 × 0,85 = 0,2064%

По таблице нормального распределения (функция Лапласа) находим, что уровню доверительной вероятности в 95% соответствует 1,65 стандартных отклонений.

VaR=1,65*(14000+20400)*0,002064=117,2 тыс.руб.

Ответ: 117200 рублей

33. Однодневный VaR портфеля инвестора с доверительной вероятностью 99% составляет 500 тыс. руб. Определить VaR портфеля для десяти дней. Предполагается, что доходность портфеля имеет нормальное распределение.

Решение:

������ = √10 × 500 = 1581138,83 рублей

Ответ: 1581138,83 рублей


38. О чем говорит показатель EaR ?
Ответ: Противоположным понятием по отношению к VaR является EaR (Earnings at Risk). EaR показывает, какую максимальную сумму дохода может принести портфель инвестора в течение определенного периода времени с заданной доверительной вероятностью.

Если доходность портфеля имеет нормальное распределение, и ее среднее значение равно нулю, то показатель EaR будет равен показателю VaR по абсолютной величине.

45. Портфель инвестора состоит из акций компании А и В. Коэффициент корреляции между доходностями акций компаний равен 0,5. Однодневный VaR с доверительной вероятностью 95% по акциям компании А равен 15 тыс. руб., по акциям компании В - 59 тыс. руб. Определить VaR портфеля из данных бумаг.

Решение:

VaR = 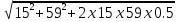= 67756,92 руб.

Ответ: 67756,92 руб.

51. Оценка стандартного отклонения акции компании А для сегодняшнего дня, сделанная вчера, равна 2,3%. Доходность акции сегодня составила 0,5%. Определить стандартное отклонение доходности для завтрашнего дня на основе модели экспоненциально взвешенной средней (EWMA). Коэффициент убывания веса принять равным 0.94.
Решение: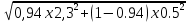
���������� = = 2,23%
Ответ: стандартное отклонение - 2,23%
57. Чему равно в Рискметриках банка J.P. Morgan значение коэффициента убывания веса в модели экспоненциально взвешенной средней (EWMA) при определении прогноза стандартного отклонения доходности актива для одного месяца?
Ответ: коэффициент убывания веса в EWMA равен 0,97.
63. Портфель состоит из акций четырех компаний. Акции куплены на суммы: Р, = 1 млн.руб.. Р_: = 3 млн.руб.. Р₃ = 5 млн.руб.. Р₄ = 6 млн.руб. Беты акций относительно фондового индекса равны: Д|=0.6; /?₂=0,75; /8з=0,9; /?4=1,2. Стандартное отклонение рыночного портфеля для одного дня составляет 1,8%. Определить однодневный VaR портфеля с доверительной вероятностью 95% согласно методике Рискметрик банка J.P. Morgan на основе стандартных факторов риска.
Решение:
��1 = 1 ÷(1 +3 + 5+ 6) = 0,066667

��2 = 3÷ (1 + 3 + 5+ 6) = 0,2

��3 = 5÷ (1 + 3 + 5+ 6) = 0,333333

��4 = 6÷ (1 + 3 + 5+ 6) = 0,4

���� = 0,066667 × 0,6 + 0,2 × 0,75 +0,333333 × 0,9 + 0,4 × 1,2 = 0,97

������ = 1,65 × 15000000 × 0,018 × 0,97 = 432135 руб.
Ответ: 432135 рублей.
69. Российский инвестор купил акции компании А на 750 тыс. долл. Коэффициент корреляции между курсом доллара и доходностью акции компании равен 0,22. Показатель VaR по акции равен 400,12 тыс. руб., по валютной позиции 97.58 тыс. руб. Определить VaR портфеля инвестора в рублях с доверительной вероятностью 95%.
Решение:
VaR = 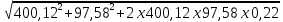= 432200 рублей
Ответ: 432200 рублей.
75. Курс доллара составляет 1 долл.=28 руб.. курс евро - 1евро =34 руб. Российский банк купил на спотовом рынке 150 тыс. долл. и купил 320 тыс. евро. Стандартное отклонение курса доллара к рублю в расчете на один день составляет 0,33%, евро к рублю - 0.42%. коэффициент корреляции между курсами долл./руб. и евро/руб. равен 0.74. Определить однодневный VaR портфеля с доверительной вероятностью 95%.
Решение:
��$ = 150 × 28 = 4200 тыс. руб.

��€ = 320 × 34 = 10880 тыс. руб.

��$ = 4200 ÷(4200 + 10880) = 0,278515

��€ = 10880 ÷ (4200 + 10880) = 0,721485

�� = √(0,278515 × 0,33) 2 + (0,721485 × 0,42) 2 − 2 × 0,278515 × 0,33 × 0,721485 × 0,42 × 0,74 = 0,243005%

������ = 1,65 × 15080 × 0,00243005 = 60464,50 рублей

Ответ: 60464,50 рублей.
81. Десятидневный VaR портфеля инвестора с доверительной вероятностью 95% составляет 300 тыс. руб. Определить VaR портфеля для доверительной вероятности 99%. Предполагается, что доходность портфеля имеет нормальное распределение.
Решение:
VaR=300/1,65 х 2,33=423636,36 рублей
Ответ: 423636,36 рублей
87. Определить однодневный EaR с доверительной вероятностью 90% для портфеля стоимостью 800 тыс. руб.. в который входят акции двух компаний. Уд. вес первой акции в стоимости портфеля составляет 35%, второй — 65%. Стандартное отклонение доходности первой акции в расчете на один день равно 1.43%. второй - 1,76%, коэффициент корреляции доходностей акций равен 0,62.
Решение:
���� = √(0,35 × 1,43) 2 +(0,65 × 1,76) 2 + 2 × 0,35 × 1,43 × 0,65 × 1,76 × 0,62 = 1,506395%

������ = 1,28 × 800 × 0,01506395 = 15425,49 рублей
Ответ: 15425,49 рублей.