Определение тока. 31 32 33 вопрос. 31 вопрос. Функциональная, статическая и корреляционная зависимость. Линейная парная регрессия
 Скачать 97.54 Kb.
|
|
31 вопрос. Функциональная, статическая и корреляционная зависимость. Линейная парная регрессия. Функциональная зависимость (связь), когда каждому значению одной переменной соответствует вполне определенное значение другой. Функциональная зависимость может иметь место как между детерминированными (неслучайными) переменными, так и между случайными величинами. Статистическая (или стохастическая, вероятностная) зависимость - каждому значению одной переменной соответствует определенное (условное) распределение другой переменной. Т.е. когда каждому значению одной переменной соответствует не какое-то определенное, а множество возможных значений другой переменной. Возникновение понятия статистической связи обусловливается тем, что зависимая переменная подвержена влиянию ряда неконтролируемых или неучтенных факторов, а также тем, что измерение значений переменных неизбежно сопровождается некоторыми случайными ошибками. В силу неоднозначности статистической зависимости между Y и Х для исследователя, в частности, представляет интерес усредненная по х схема зависимости, т.е. закономерность в изменении среднего значения - условного математического ожидания  (математического ожидания случайной переменнойY, вычисленного в предположении, что переменная Х приняла значение х) в зависимости от х.Определение. Статистическая зависимость между 2мя переменными, при которой каждому значению 1 переменной соответствует определенное условное математическое ожидание (среднее значение) другой, называется корреляционной. Иначе, корреляционной зависимостью между двумя переменными величинами называется функциональная зависимость между значениями одной из них и условным математическим ожиданием другой. Иначе, корреляционной зависимостью между двумя переменными величинами называется функциональная зависимость между значениями одной из них и условным математическим ожиданием другой. +Корреляционная зависимость м.б. представлена в виде:  Сравнивая различные виды зависимости между Х и Y, можно сказать, что с изменением значений переменной Х при функциональной зависимости однозначно изменяется определенное значение переменной Y, при корреляционной - определенное среднее значение (условное математическое ожидание) Y, а при статистической - определенное (условное) распределение переменной Y. Т.о., из рассмотренных зависимостей наиболее общей выступает статистическая зависимость. Каждая корреляционная зависимость является статистической, но не каждая статистическая зависимость является корреляционной. Функциональная зависимость представляет частный случай корреляционной. Уравнение парной линейной регрессии для генеральной совокупности можно построить, если доступны данные обо всех элементах генеральной совокупности. На практике данные всей генеральной совокупности недоступны, но доступны данные об элементах некоторой выборки. Поэтому параметры генеральной совокупности оценивают при помощи соответствующих параметров соответствующей выборки: свободный член прямой парной линейной регрессии генеральной совокупности  заменяют на свободный член прямой парной линейной регрессии выборки  , а коэффициент направления прямой парной линейной регрессии генеральной совокупности - на коэффициент направления прямой парной линейной регрессии выборки  . 32 вопрос. Выборочный коэффициент корреляции и его свойства. Выборочный коэффициент корреляции является одним из основных показателей тесноты связи между двумя переменными. При изучении зависимости переменной Y от переменной Х выборочный коэффициент корреляции обозначается как rxy. При изучении зависимости переменной Х от переменной Y выборочный коэффициент корреляции обозначается как ryx. Выборочный коэффициент корреляции является оценкой коэффициента корреляции Pxy генеральной совокупности. Выборочный парный коэффициент корреляции ryx:  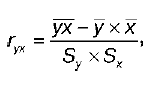 где ух – среднее арифметическое произведения факторной и результативной переменных: 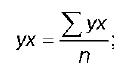 S y – выборочное среднеквадратическое отклонение результативной переменной у , показывающее, на сколько единиц в среднем отклоняются значения результативной переменной у от ее среднего значения y–: 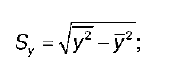 у 2 – среднее значение из квадратов значений результативной переменной у : y2 – квадрат средних значений результативной переменной у : S x – выборочное среднеквадратическое отклонение факторной переменной х, показывающее, на сколько единиц в среднем отклоняются значения факторной переменной х от ее среднего значения x : 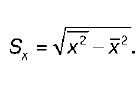 Выборочный коэффициент корреляции обладает следующими свойствами: 1) по абсолютной величине выборочный коэффициент корреляции не превосходит единицы: | r yx | ≤ 1, или –1 ≤ ryx ≤ 1; 2) если ryx = 0, т. е. выборочный коэффициент корреляции равен нулю, то переменные Y и Х не связаны статистической зависимостью. В этом случае проведение регрессионного анализа между исследуемыми переменными считается нецелесообразным; 3) если |ryx| = 1, т. е. выборочный коэффициент корреляции по абсолютной величине равен единице, то наблюдаемые значения исследуемых переменных связаны линейной функциональной зависимостью; 4) `если выборочный коэффициент корреляции принадлежит интервалу от нуля до единицы, то связь между исследуемыми переменными прямая; если же выборочный коэффициент корреляции принадлежит интервалу от нуля до минус единицы, то связь между исследуемыми переменными обратная. 33 вопрос. Корреляционная таблица. Отыскание параметров выборочного уравнения прямой линии регрессии по сгруппированным данным. Корреляционная таблица таблица сопряженности признаков) один из основных способов описания корреляционных связей между признаками, используемых для упорядочения информации о распределении изучаемой совокупности индивидов по двум признакам. К. т. имеет прямоугольную форму, число строк ее nопределяется количеством значений одного признака, а число столбцов m количеством значений другого. На пересечении, например, второй строки и третьего столбца в таблице проставляется число индивидов, у которых первый признак принимает второе значение из своего списка, а второй признак третье из своего Построение корреляционной таблицы начинают с группировки значений фактического и результативного признаков. Для этого надо разбить все данные значения на требуемое количество интервалов (если количество интервалов не оговаривается в задании, можно выбрать k = 7, 8 или 10). Длина интервала вычисляется по формулам  где k — количество интервалов. В первый столбик следует вписать значения факторного признака (X), а первую строку заполнить значениями результативного признака (Y).
 Параметры pyx и В, которые определяются методом наименьших квадратов, имеют вид: где yx — условная средняя; XВ и Ув — выборочные средние признаков X и У; —x и —у — выборочные средние квадратические отклонения; гВ — выборочный коэффициент корреляции. Выборочное уравнение прямой линии регресии X на У имеет вид:  Считаем, что данные наблюдений над признаками X и У заданы в виде корреляционной таблицы с равноотстоящими вариантами. Тогда переходим к условным вариантам: 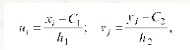 где С1 — варианта признака X, имеющая наибольшую частоту; С 2 — варианта признака У, имеющая наибольшую частоту; h1 — шаг (разность между двумя соседними вариантами X); h2 — шаг (разность между двумя соседними вариантами У). Тогда выборочный коэффициент корреляции  Величины u, v, su, sv могут быть найдены методом произведений, либо непосредственно по формулам  Зная эти величины, найдем параметры, входящие в уравнения регрессии, по формулам  |