Эконометрика лекция!!!. Лекция Корреляционнорегрессионный анализ. Парная регрессия
 Скачать 380.5 Kb.
|
|
Лекция 2. Корреляционно-регрессионный анализ. Парная регрессия 1. Сущность корреляционно-регрессионного анализа и его задачи. 2. Определение регрессии и ее виды. 3. Особенности спецификации модели. Причины существования случайной величины. 4. Методы выбора парной регрессии. 5. Метод наименьших квадратов. 6. Показатели измерения тесноты и силы связи. 7. Оценки статистической значимости. 8. Прогнозируемое значение переменной у и доверительные интервалы прогноза. 1. Сущность корреляционно-регрессионного анализа и его задачи. Экономические явления, будучи весьма разнообразными, характеризуются множеством признаков, отражающих определенные свойства этих процессов и явлений и подверженных взаимообусловленным изменениям. В одних случаях зависимость между признаками оказывается очень тесной (например, часовая выработка работника и его заработная плата), а в других случаях такая связь не выражена вовсе или крайне слаба (например, пол студентов и их успеваемость). Чем теснее связь между этими признаками, тем точнее принимаемые решения. Различают два типа зависимостей между явлениями и их признаками:
Частным случаем статистической зависимости является корреляционная зависимость. Корреляционная зависимость – это связь, при которой каждому значению независимой переменной х соответствует определенное математическое ожидание (среднее значение) зависимой переменной у. Корреляционная зависимость является «неполной» зависимостью, которая проявляется не в каждом отдельном случае, а только в средних величинах при достаточно большом числе случаев. Например, известно, что повышение квалификации работника ведет к росту производительности труда. Это утверждение часто подтверждается на практике, но не означает, что у двух и более работников одного разряда / уровня, занятых аналогичным процессом, будет одинаковая производительность труда. Корреляционная зависимость исследуется с помощью методы корреляционного и регрессионного анализа. Корреляционно-регрессионный анализ позволяет установить тесноту, направление связи и форму этой связи между переменными, т.е. ее аналитическое выражение. Основная задача корреляционного анализа состоит в количественном определении тесноты связи между двумя признаками при парной связи и между результативными и несколькими факторными признаками при многофакторной связи и статистической оценке надежности установленной связи. 2. Определение регрессии и ее виды. Регрессионный анализ является основным математико-статистическим инструментом в эконометрике. Регрессией принято называть зависимость среднего значения какой-либо величины (y) от некоторой другой величины или от нескольких величин (xi). В зависимости от количества факторов, включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессии. Простая (парная) регрессия представляет собой модель, где среднее значение зависимой (объясняемой) переменной у рассматривается как функция одной независимой (объясняющей) переменной х. В неявном виде парная регрессия – это модель вида:  .В явном виде:  ,где a и b – оценки коэффициентов регрессии. Множественная регрессия представляет собой модель, где среднее значение зависимой (объясняемой) переменной у рассматривается как функция нескольких независимых (объясняющих) переменных х1, х2, … хn. В неявном виде парная регрессия – это модель вида:  .В явном виде:  ,где a и b1, b2, bn – оценки коэффициентов регрессии. Примером такой модели может служить зависимость заработной платы работника от его возраста, образования, квалификации, стажа, отрасли и т.д. Относительно формы зависимости различают:
3. Особенности спецификации модели. Причины существования случайной величины. Любое эконометрическое исследование начинается со спецификации модели, т.е. с формулировки вида модели, исходя из соответствующей теории связи между переменными. Прежде всего из всего круга факторов, влияющих на результативный признак, необходимо выделить наиболее существенно влияющие факторы. Парная регрессия достаточна, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной. Уравнение простой регрессии характеризует связь между двумя переменными, которая проявляется как некоторая закономерность лишь в среднем в целом по совокупности наблюдений. В уравнении регрессии корреляционная связь представляется в виде функциональной зависимости, выраженной соответствующей математической функцией. Практически в каждом отдельном случае величина у складывается из двух слагаемых:  ,где у – фактическое значение результативного признака;  – теоретическое значении результативного признака, найденное исходя из уравнения регрессии; – случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.Случайная величина называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Присутствие в модели случайной величины порождено тремя источниками:
К ошибкам спецификации будут относиться не только неправильный выбор той или иной математической функции, но и недоучет в уравнении регрессии какого-либо существенного фактора (использование парной регрессии вместо множественной). Наряду с ошибками спецификации могут иметь место ошибки выборки, поскольку исследователь чаще всего имеет дело с выборочными данными при установлении закономерностей связи между признаками. Ошибки выборки имеют место и в силу неоднородности данных в исходной статистической совокупности, что, как правило, бывает при изучении экономических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла. Для получения хорошего результата обычно исключают из совокупности единицы с аномальными значениями исследуемых признаков. И в этом случае результаты регрессии представляют собой выборочные характеристики. Исходных данных Однако наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели (вид математической формулы), а ошибки выборки – увеличивая объем исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками. 4. Методы выбора парной регрессии. Предполагая, что ошибки измерения сведены к минимуму, основное внимание в эконометрических исследованиях отводится ошибкам спецификации модели. В парной регрессии выбор вида математической функции может быть осуществлен тремя методами:
При изучении зависимости между двумя признаками графический метод подбора вида уравнения регрессии достаточно нагляден. Он основан на поле корреляции. Основные типы кривых, используемых при количественной оценке связей  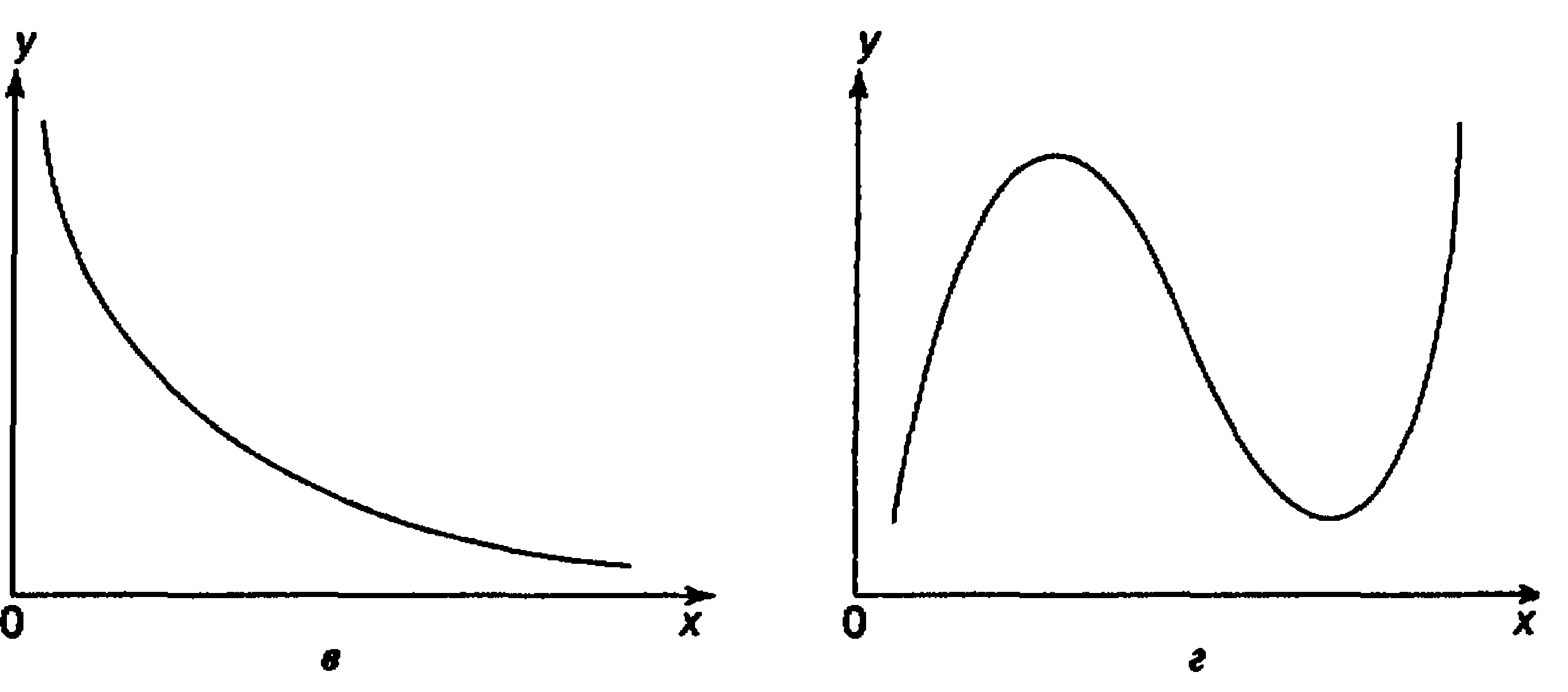 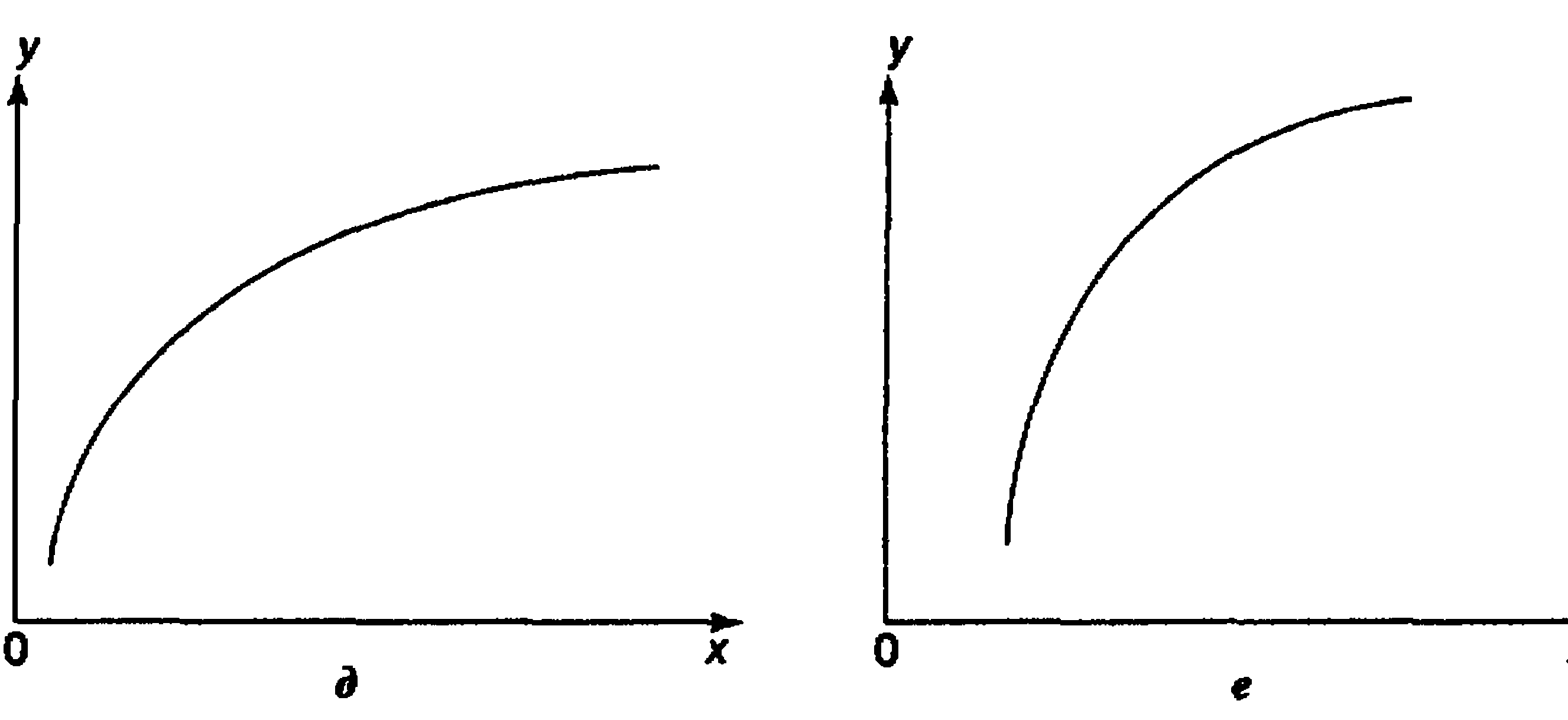        Класс математических функций для описания связи двух переменных достаточно широк, также используются и другие типы кривых. Аналитический метод выбор типа уравнения регрессии основан на изучении материальной природы связи исследуемых признаков, а также визуальной оценке характера связи. Т.е. если мы говорим о кривой Лаффера, показывающей зависимость между прогрессивностью налогообложения и доходами бюджета, то речь идет о параболической кривой, а в микроанализе изокванты представляют собой гиперболы. 5. Метод наименьших квадратов. Линейная регрессия находит широкое применение в эконометрике в виду четкой экономической интерпретации ее параметров и сводится к нахождению уравнения вида:  ,где х – объясняющая (независимая) переменная – неслучайная величина; у – объясняемая (зависимая) величина; – случайный член (ошибка регрессии); и β – параметры уравнения. Теоретические значения  представляют линию регрессии. Построение линейной регрессии сводится к оценке параметров a и b уравнения .Оценки параметров линейной регрессии могут быть найдены разными способами. Метод наименьших квадратов (МНК) – классический подход к оцениванию параметров линейной регрессии. Обратимся к полю корреляции.  По графику можно определить значения параметров. Параметр а – точка пересечения линии регрессии с осью Оу, а параметр b оценивается исходя из угла наклона линии регрессии  , где dy – приращение фактора у, а dx – приращение фактора х.МНК позволяет получить такие оценки параметров a и b, при которых сумма квадратов отклонений фактических значений результативного признака у от расчетных (теоретических) значений минимальна: Т.е. линия регрессии выбирается таким образом, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальна.    ,где .Вычислим частные производные по каждому из параметров a и b.  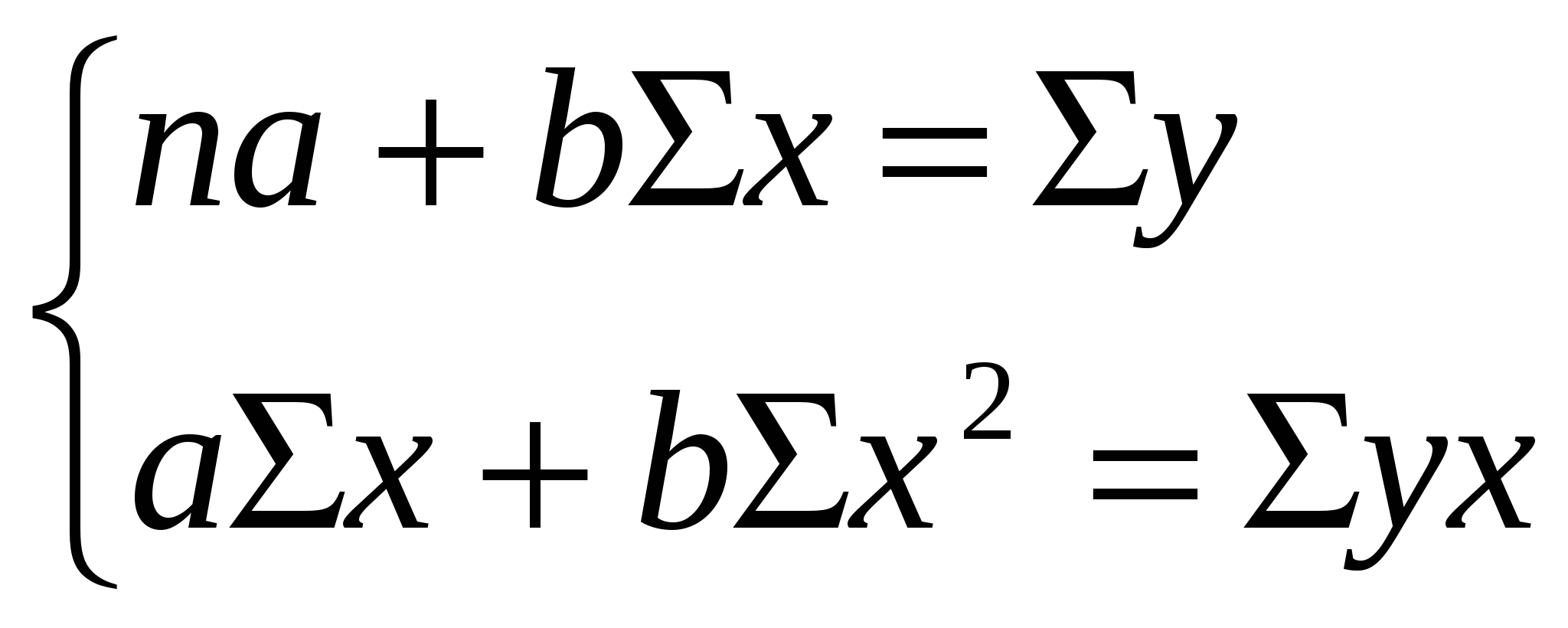 Разделим обе части уравнений на n и получим систему уравнений, из которой можно вычислить оба параметра. 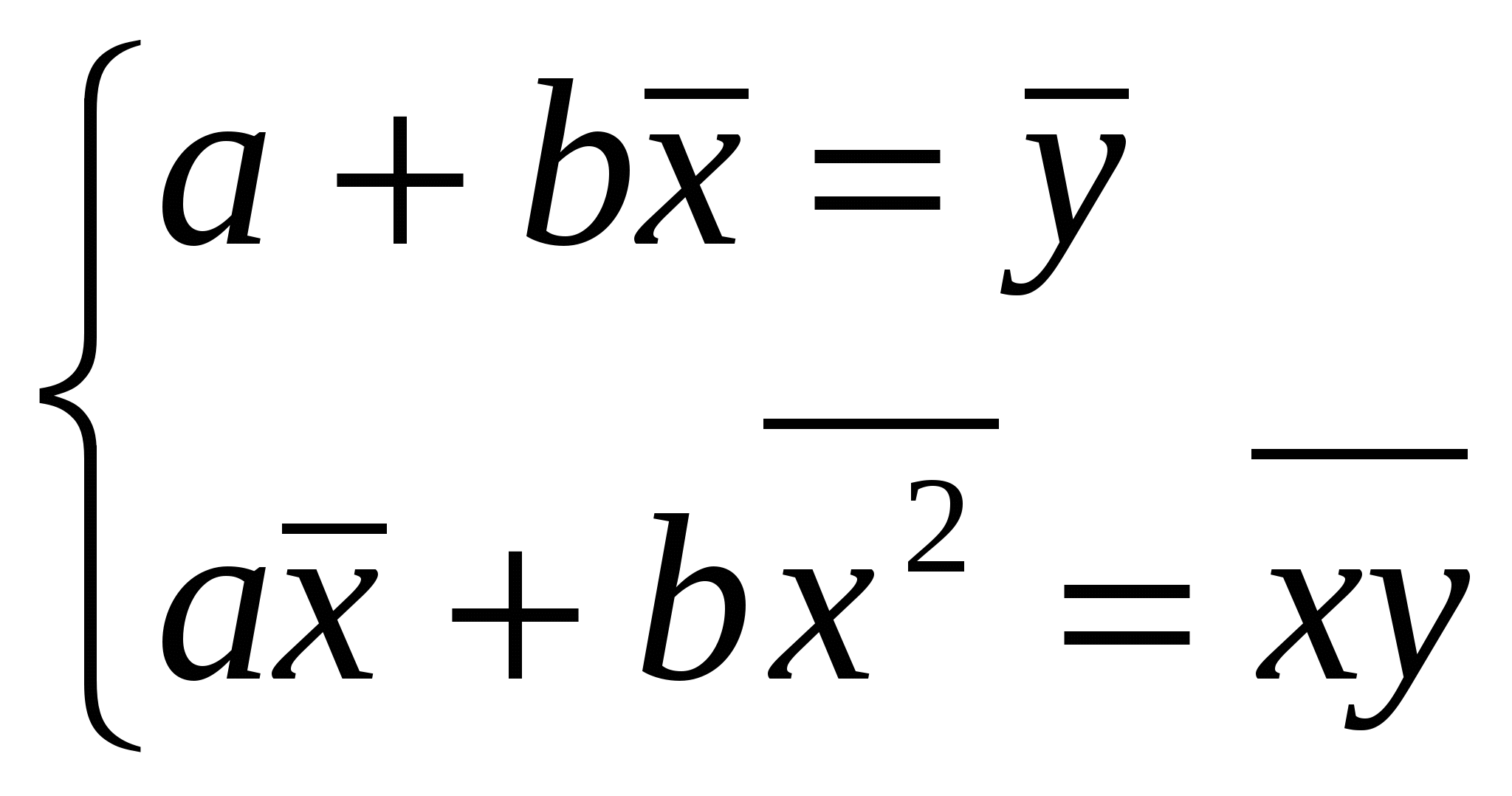 Из МНК можно получить две другие формулы для нахождения параметра b: 1.  2.  или  Оценка параметра а находится одинаковым способом во всех случаях:  .Параметр b называется коэффициентом регрессии и показывает, на сколько единиц в среднем изменится переменная у при увеличении переменной х на 1 единицу. Знак при коэффициенте регрессии показывает направление связи: при b < 0 – связь обратная, при b > 0 – связь прямая. Параметр а формально представляет собой значение у при х = 0. Если х не имеет или не может иметь нулевого значения, то а не имеет смысла. Он может и не иметь экономического смысла. При а<0 экономическая интерпретация может оказаться абсурдной. Интерпретировать можно знак при параметре а. Если а>0, то относительное изменение результата происходит медленнее, чем изменение фактора. Если а<0, то изменение результата опережает изменение фактора. 6. Показатели измерения тесноты и силы связи. Уравнение регрессии всегда дополняется показателем тесноты связи. Качество парной регрессии определяется с помощью парного линейного коэффициента корреляции:  или , где  , – среднеквадратические отклонения, которые показывают разброс значений в множестве значений х и у. Большое значение среднеквадратического отклонения показывает большой разброс значений в представленном множестве со средней величиной множества; маленькое значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.Линейный коэффициент корреляции находится в пределах: -1 <  < 1.Если коэффициент корреляции положительный (рис. а), то связь между признаками прямая, т.е. с увеличением (уменьшением) x признак y увеличивается (уменьшается). Если коэффициент корреляции отрицательный (рис. б), то связь между признаками обратная, т.е. с увеличением (уменьшением) x признак y уменьшается (увеличивается). 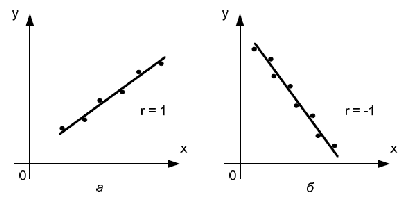 Чем ближе значение коэффициента корреляции к 1, тем теснее связь (рис. б), чем ближе к 0, тем слабее (рис. а).  Если 0 < | | <0,3, то связь между признаками практически отсутствует, если 0,3 < | | <0,5, то связь слабая,если 0,5 < | | <0,7, то связь умеренная,если 0,7 < | | <1, то связь сильная.И, наконец, при r = 0 линейная корреляционная связь отсутствует. При этом линия регрессии параллельна оси Ох. 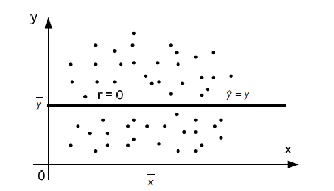 Следует отметить, что величина линейного коэффициента корреляции оценивает тесноту связи рассматриваемых признаков в ее линейной форме. Поэтому близость абсолютной величины коэффициента корреляции к нулю еще не означает отсутствие связи между признаками. При иной спецификации модели связь между признаками может оказаться достаточно тесной. Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции R2, называемый коэффициентом детерминации. Он характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака. 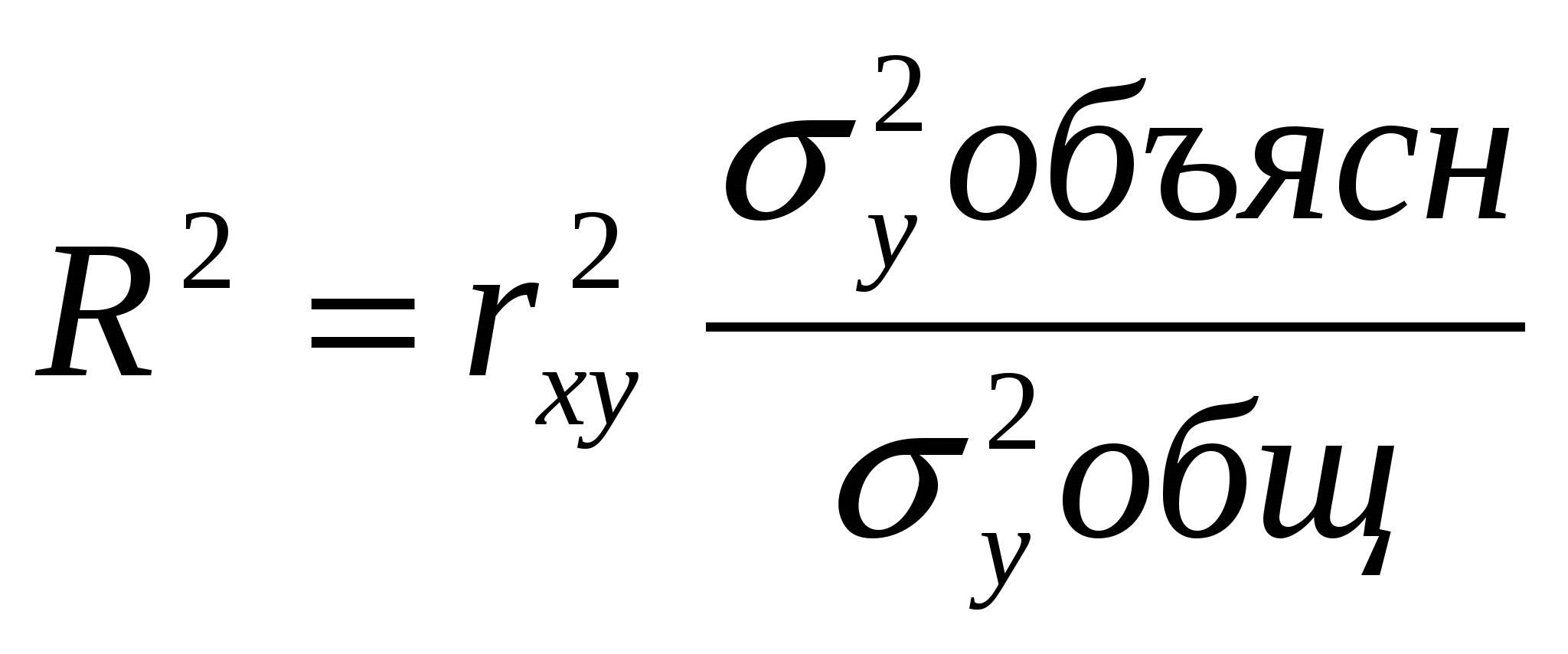 Соответственно величина 1 – R2 характеризует долю дисперсии у, вызванную влиянием остальных не учтенных в модели факторов. В силу своего определения R2 принимает значения между 0 и 1, т.е. 0 ≤ R2 ≤ 1. Если R2 = 0, то это означает, что регрессия ничего не дает, т.е х не улучшает качество предсказания у по сравнению с тривиальным предсказанием  .Другой крайний вариант R2 = 1 означает точную подгонку модели: все точки наблюдений лежат на регрессионной прямой (все =0). Чем ближе R2 к 1, тем лучше качество подгонки модели и тем точнее  .Параметре регрессии b хотя и показывает, на сколько единиц в среднем изменится переменная у при увеличении переменной х на 1 единицу, но использовать для непосредственной оценки влияния факторного признака на результативный нельзя из-за различия единиц измерения исследуемых показателей. Для этих целей используют коэффициент эластичности. Коэффициент эластичности показывает, на сколько процентов изменяется результативный признак у при изменении факторного признака х на 1%, и вычисляется по формуле:  ,где  – первая производная, характеризующая соотношение приростов результата и фактора для соответствующей формы связи.В силу того того, что коэффициент эластичности для линейной функции не является величиной постоянной, а зависит от соответствующего значения х, то обычно рассчитывается средний коэффициент эластичности:  .Несмотря на широкое использование в эконометрике коэффициентов эластичности, возможны случаи, когда их расчет не имеет экономического смысла. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения значений в процентах (например, на сколько процентов изменится урожайность пшеницу, если качество почвы улучшится на 1%). Коэффициенты эластичности для ряда математических функций  7. Оценки статистической значимости. После того как найдено уравнение регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров. Оценка значимости уравнения в целом. Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера и служит для выяснения того, что полученное значение коэффициента детерминации  неслучайно, т.е. соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.В парной линейной регрессии проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии. Для проверки значимости уравнения регрессии в целом используют F-критерий Фишера. В случае парной линейной регрессии значимость модели регрессии проверяется по следующей формуле:  ,где m – количество объясняющих факторных признаков, т.е. х. Наблюдаемые значения сравниваются с табличными.  ,где α – уровень значимости, соответствующий доверительному интервалу; k1 = m k2 = n–m–1 Если при заданном уровне значимости Fнабл > Fкрит, то модель считается значимой, гипотеза о случайной природе оцениваемых характеристик отрицается и признается их статистическая значимость и надежность. Если Fнабл < Fкрит, то коэффициент детерминации считается незначимым, что дает основание считать, что влияние объясняющей переменной х в модели несущественно, а, следовательно, общее качество модели невысокое. Стандартная ошибка оценки уравнения регрессии. Хотя МНК дает нам линию регрессии, которая обеспечивает минимум вариации, не все наблюдения совпадают с линией регрессии. Поэтому необходима статистическая мера вариации фактических значений у от предсказанных значений . Мера вариации относительно линии регрессии называется стандартной ошибкой оценки.Стандартная ошибка оценки определяется как:  ,где у – фактические значения зависимой переменной для заданных значений независимой переменной; – теоретические / предсказанные значения зависимой переменной для заданных значений независимой переменной;m – количество объясняющих переменных х. Данный коэффициент характеризует меру вариации фактических данных вокруг линии регрессии. Проверка значимости параметров. Кроме того, проверяется значимость параметров регрессии. Проверка значимости параметров отдельных коэффициентов регрессии проводится по t-критерию Стьюдента путем проверки гипотезы о равенстве нулю каждого коэффициента регрессии. При этом выясняют, не являются ли полученные значения параметров результатом действия случайных величин. Значимость коэффициентов регрессии проверяется по следующим формулам. Для коэффициента b:  ,где Sb – стандартная ошибка коэффициента b, которая в свою очередь определяется как:  .Для коэффициента а аналогично:  ,где Sa – стандартная ошибка свободного члена а, также находится по формуле:  .Расчетные значения t-критерия сравниваются с табличным значением критерия  , где k = n–m–1 степеням свободы и соответствующем уровне значимости α.Если расчетное значение t-критерия превосходит его табличное значение, то параметр признается значимым, т.е. не является случайно найденным. 8. Прогнозируемое значение переменной у и доверительные интервалы прогноза. Точечный прогноз заключается в получении прогнозного значения Y*, которое определяется путем подстановки в уравнение регрессии соответствующего прогнозного значения X*: .Вероятность реализации точечного прогноза практически равна нулю, поэтому рассчитывается доверительный интервал прогноза с большей надежностью. Интервальный прогноз заключается в построении доверительного интервала прогноза, т.е. нижней и верхней – минимально и максимально возможных границ интервала, содержащего точную величину для прогнозного значения Y* с заданной вероятностью, т.е.: Уmin < Y* < Ymax. Доверительные интервалы прогноза определяются по следующим формулам:  ,где 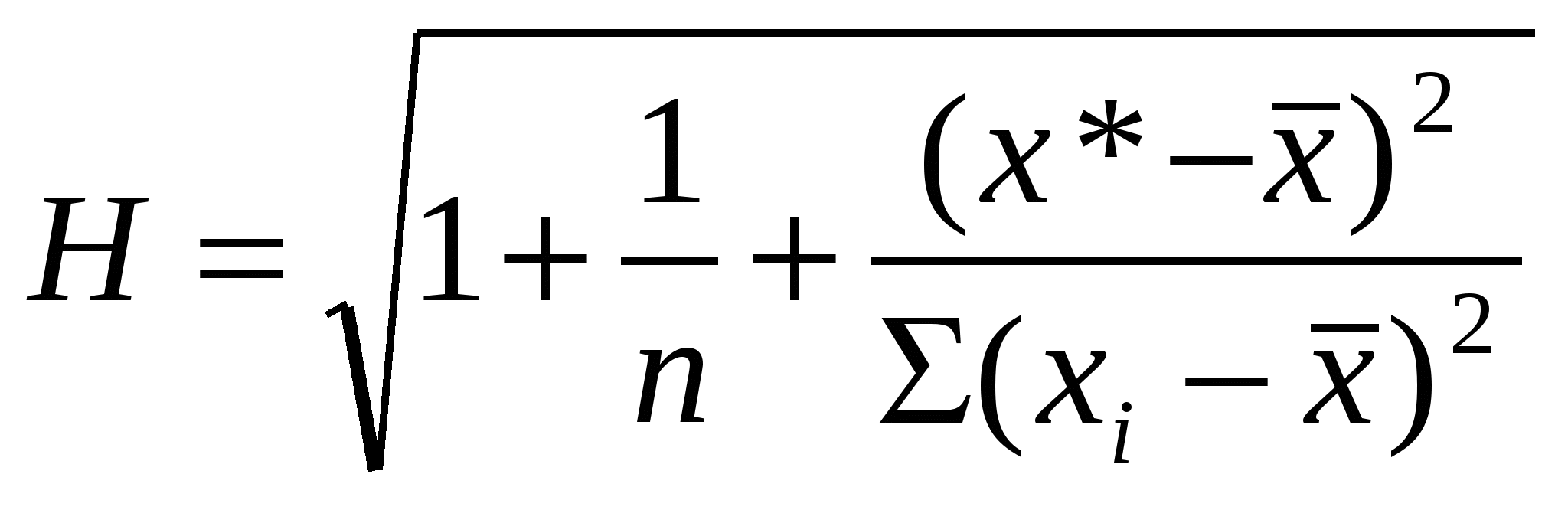 – стандартная ошибка предсказаний для парной регрессии.Доверительный интервал для коэффициентов регрессии определяются как:  и .Так как коэффициент регрессии в эконометрических исследованиях имеет четкую экономическую интерпретацию, то доверительные границы интервала для коэффициента регрессии не должны содержать противоречивых результатов, например, -10b40 – такого рода запись указывает на то, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего быть не может. Тогда параметр принимается равным нулю. |