Финансовые расчеты. 38. 03. 01 Экономика Учебная дисциплина Основы финансовых расчётов
 Скачать 37.49 Kb. Скачать 37.49 Kb.
|
|
Министерство образования и науки Российской Федерации ФГАОУ ВО «Севастопольский государственный университет» Институт финансов, экономики и управления Направление 38.03.01 –Экономика Учебная дисциплина «Основы финансовых расчётов» ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 1Предмет, метод и задачи финансовой математики Финансовая математика — раздел прикладной математики, имеющий дело с математическими задачами, связанными с финансовыми расчётами. Предмет: финансовые и актуарные оценки эффективности операций, сделок, их участие на основе процентных ставок, дисконта, индекса рентабельности, коэффициента приращения и дисконтирования, дивидендных выплат Виды финансовых операций: 1 Предоставление кредита клиенту коммерческого банка 2 Предоставление имущества в лизинг 3 Размер денежных средств во вклада, депозит 4 Учет векселя в коммерческом банке 5 Инвестиции денежных средств в ценные бумаги Период начисления процентов представляет собой временной отрезок между последующими взиманиями процентов Основные задачи: - измерение конечных финансовых результатов финансовой операции для каждой из участвующих сторон; - разработка планов выполнения финансовых операций, в т. ч. планов погашения задолженности; - измерение зависимости в конечных результатах операции от основных ее параметров; - определение допустимых критических значений показателей и расчет параметров эквивалентного (без убыточного) изменения первоначальных условий финансовой операции. Расчеты по простым процентам Процентная ставка – это отношение суммы процентных денег, выплачиваемых за строго фиксированный отрезок времени, к величине кредита, ссуды и прочее. Ставки процентов могут применяться к одной и той же начальной сумме на протяжении всего срока действия кредита, ссуды. Такого рода проценты называются простыми процентными ставками Интервал времени, к которому относится процентная ставка, называют периодом начисления Начисление процентов, как правило, производится дискретно, т.е. в отдельные (обычно равноотстоящие) моменты времени (дискретные проценты), причем, в качестве периодов начисления принимают год, полугодие, квартал, месяц. Иногда практикуют ежедневное начисление, а в ряде случаев удобно применять непрерывные проценты. 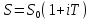    Наращенная сумма – это первоначальная сумма вместе с начисленными к концу срока операции процентами. 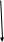 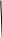 S  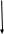 S0  1 2 T График наращения по методу простых процентов Вексель выдан на 12 000 руб. со сроком уплаты 03 июня. Владелец учёл его в банке 15 апреля по учётной ставке 8,5%. Определите сумму, полученную предъявителем векселя и доход банка при реализации дисконта. Т=16+31+2=49 S = 12000(1- (49/360)*0,85) = 10611,67(фр практика) Сумма получ пред векселя D =12000 – 10611,67=1399,33 Доход банка Утверждены на заседании кафедры _________ «Финансы и кредит»____________ ____________________________протокол № 1 от ______________ Зав. кафедрой _________Чайкина Е.В. Экзаменатор _____________Ситникова О. Г, |
