4 бескоалиционные(некооперативные) игры
 Скачать 261.08 Kb. Скачать 261.08 Kb.
|
.
Очевидно, ни одна из чистых стратегий первого игрока не доминируется иными чистыми стратегиями. Что можно сказать о смешанных стратегиях? Не составляет труда убедиться в том, что выбирая смешанную стратегию 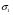 =( 0.5, 0, 0.5), игрок 1 гарантирует себе выигрыш 5.5 вне зависимости от того, каким будет ход второго игрока: U1( 0.5, 0, 0.5; L)= 0.5(9)+ 0.5(2) = 5.5 =( 0.5, 0, 0.5), игрок 1 гарантирует себе выигрыш 5.5 вне зависимости от того, каким будет ход второго игрока: U1( 0.5, 0, 0.5; L)= 0.5(9)+ 0.5(2) = 5.5 U1(0.5, 0, 0.5; R)= 0.5(1)+ 0.5(10) = 5.5 Подобная смешанная стратегия отчетливо доминирует чистую стратегию M. Эти соображения делают логичным переход к иному определению доминируемой стратегии, предполагающему возможность использования смешанных стратегий. Def.2 Чистая стратегия i-го игрока  в игре G является строго доминируемой, если существует смешанная стратегия в игре G является строго доминируемой, если существует смешанная стратегия 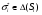 , такая, что для всех , такая, что для всех  Ui( Ui(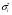 , s-i)>Ui(si, s-i) , s-i)>Ui(si, s-i) и слабо доминируемой , если Ui( 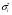 , s-i) ≥ Ui(si, s-i ) , s-i) ≥ Ui(si, s-i )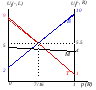
Обозначенные на рисункетринаклонныелинии представляют собой совокупность точек, соответствующих выпуклым комбинациям выигрышей при выборе первым игроком той или иной стратегии( Т, М и В). Очевидно, что игроку 1 следует выбирать(обратите внимание на жирные линии) • стратегию Т, если он полагает, что вероятность того, что второй игрок выберет стратегию R, т.е. р(R) < 7/16 , • стратегию В , если он ожидает, что р(R) > 7/16 , • ему безразлично какую из стратегий(Т или В) выбрать, если он полагает, р(R) = 7 /16(ожидаемая полезность в обоих случаях составит 88/16= 5.5) . Соответственно, и любая выпуклая комбинация этих стратегий будет обеспечивать индивиду получение той же самой ожидаемой полезности. Поскольку линия, соответствующая стратегии М , лежит ниже жирной ломанной линии, она никогда не окажется предпочтительнее прочих чистых и части основанных на них смешанных стратегий. Именно части этих смешанных старатегий. Действительно, если р(R) = 7/16, то любая смешанная стратегия аT+(1-а)B предпочтительнее стратегии М, но при иных ожиданиях, например, при р(R) = 1 смешанная стратегия 0.9T+0.1B обеспечивает уровень ожидаемой полезности 1.1, что меньше 4 .
Нам остается определить множество смешанных стратегий, доминирующих стратегию M . Обозначим 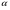 вероятность того, что игрок 1 выберет нижнюю строку(т.е. стратегию B), соответственно, вероятность выбора им верхней строки будет равна (1 - вероятность того, что игрок 1 выберет нижнюю строку(т.е. стратегию B), соответственно, вероятность выбора им верхней строки будет равна (1 -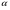 ) )В зависимости от выбора вторым игроком стратегии Lили Rожидаемые полезности игрока 1 от использования смешанной стратегии (T +В) будут равны: если игрок 2 выберет L : U1(T+B, L)=9(1- 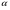 )+2 )+2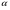 ; ;если игрок 2 выберет R: U1(T+B, R)=1(1- 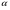 )+10 )+10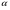 Выпишем условия, выполнение которых необходимо для того, чтобы смешанные стратегии, основанные на чистых стратегиях Т и В , доминировали бы стратегию М:
Итак, чистая стратегия М строго доминируется смешанными стратегиями, основывающихся на чистых стратегиях Т и В, такими, что 1/3 < 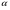 < 4/7. Соединив прямой линией точки, соответствующие стратегиям Т и В на рисунке 4.2.б, мы увидим, что найденному диапазону вероятностей будет соответствовать отрезок этой линии, лежащий одновременно и выше и правее точки М(все тот же северо-восточный угол)). Все эти рассуждения о доминировании чистой стратегии смешанными носят отнюдь не отвлеченный характер( например, в этой связи вполне уместно вновь вспомнить о диверсификации риска, о портфельных инвестициях и пр). < 4/7. Соединив прямой линией точки, соответствующие стратегиям Т и В на рисунке 4.2.б, мы увидим, что найденному диапазону вероятностей будет соответствовать отрезок этой линии, лежащий одновременно и выше и правее точки М(все тот же северо-восточный угол)). Все эти рассуждения о доминировании чистой стратегии смешанными носят отнюдь не отвлеченный характер( например, в этой связи вполне уместно вновь вспомнить о диверсификации риска, о портфельных инвестициях и пр). Разумеется доминируемой может быть и смешанная стратегия и еще более общее определение может выглядеть следующим образом: Def.3 Стратегия i-го игрока  в игре G является строго доминируемой, если существует смешанная стратегия в игре G является строго доминируемой, если существует смешанная стратегия 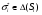 , такая, что для всех , такая, что для всех 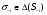 Ui( Ui(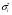 , ,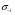 )>Ui( )>Ui(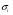 , ,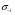 ) )и слабо доминируемой , если Ui( 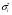 , ,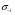 ) ) 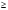 Ui( Ui(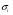 , ,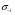 ) )1.3. РАВНОВЕСИЕ ПО НЭШУ В ЧИСТЫХ СТРАТЕГИЯХ. НАИЛУЧШАЯ РЕАКЦИЯ (BESTRESPONSE). ПРИМЕР: РАВНОВЕСИЕ ПО КУРНО. Def. Профиль( сочетание) чистых стратегий игроков s*=(s1*, s2*, ..., sn*) является равновесным по Нэшу(NE - Nashequilibrium) в чистых стратегиях, если для любого игрока i, i=1,...I Ui(si*, s-i*) ≥ Ui(si, s-i*) для всех si  Si . Si .Поиск состояний,равновесных по Нэшу . Рассмотрим метод, основанный на выделении наилучшей реакции одного игрока на каждый из возможных ходов(стратегий) другого(bestresponse). В приведенной ниже платежной матрице подчеркнем все такие наилучшие реакции. Клеточке, содержащей два подчеркнутых элемента, соответствует равновесное по Нэшу сочетание стратегий игроков.
Любое иное сочетание стратегий помимо (1,1) не будет равновесным, ибо игроки, узнав о ходе партнера, будут стремиться отклониться от ранее выбранной стратегии. Например, рассмотрим пару стратегий (3,2). Игрок 2 будет сожалеть о том, что он не выбрал стратегию 1, в то время как игрок 1, будет сожалеть о том, что он не выбрал стратегию 2. Лишь в том случае, когда оба игрока выберут первые стратегии, ни один из них не пожалеет о сделанном выборе, ибо эти стратегии являются лучшей реакцией друг на друга. Возможная неединственность равновесий по Нэшу: "БИТВА ПОЛОВ" ИЛИ "СЕМЕЙНЫЙ СПОР" (BATTLE OF SEXES)
Пример игры, не имеющей равновесий по Нэшу в чистых стратегиях:
Бесконечность чистых стратегий, естественным образом, требует определения функций реакции. Более точно их следовало бы назвать функциями (наилучшей или оптимальной) реакции, поскольку получение такого рода функций предполагает решение каждым из игроков задачи оптимизации, в которой в качестве переменной фигурирует стратегия партнера(будь то выбранный им уровень цены или объем выпуска). Функция реакции, тем самым, предписывает игроку некий оптимальный тип поведения с учетом всех возможных стратегий партнера по игре, а равновесие по Нэшу ( в том случае, если оно существует), может быть получено при решении системы уравнений, объединяющей подобные функции реакции. Пример равновесия по Нэшу в чистых бесконечных стратегиях (равновесие по Курно). Будем полагать, что фирмы нейтральны к риску и ориентируются на максимизацию прибыли  i(q1, q2) = p(q1+ q2)qi- Ci(qi) Предположим, что кривая рыночного спроса линейна и имеет единичный наклон, а предельные издержки фирм всех постоянны и равны некоей константе с (фиксированные затраты при этом будем полагать равными нулю): p(q1+ q2)= max { 0, a - (q1 + q2 ) i(q1, q2) = p(q1+ q2)qi- Ci(qi) Предположим, что кривая рыночного спроса линейна и имеет единичный наклон, а предельные издержки фирм всех постоянны и равны некоей константе с (фиксированные затраты при этом будем полагать равными нулю): p(q1+ q2)= max { 0, a - (q1 + q2 )Ci(qi)= с qi, где 0 ≤ с ≤ a q1*= r1(q2)=argmax [p(q1+ q2)q1 - с q1] =(a - q2 - с)/ 2; q2 *= r2(q1)=argmax[p(q1+ q2)q2 - с q2] =(a - q1 - с)/ 2 Решив их совместно, получимq1*= q2* = (a - c)/3 1.4. РАВНОВЕСИЕ ПО НЭШУ В СМЕШАННЫХ СТРАТЕГИЯХ. ИНДИФФЕРЕНТНОСТЬ ИГРОКА К ВЫБОРУ СТРАТЕГИЙ:ИНТЕРПРЕТАЦИЯ СМЕШАННЫХ СТРАТЕГИЙ. СУЩЕСТВОВАНИЕ РАВНОВЕСИЯ ПО НЭШУ В СМЕШАННЫХ СТРАТЕГИЯХ: ТЕОРЕМА НЭША. Def. Профиль смешанных стратегий *=(1*,2*, ...,I*) ,где i *Si) - равновесная смешанная стратегия игрока i- игрока, образует равновесие по Нэшу , если для любого i=1,...IUi(i *, -i*) ≥ Ui(si, -i* ) для всех siSi. Каждая из равновесных смешанных стратегий - bestresponse. Для биматричных игр: равновесие по Нэшу - это пара смешанных стратерий, такая, что равновесная смешанная стратегия одного игрока максимизирует ожидаемую полезность другого. Игрок выбирает смешанную стратегию, максимизирующую полезность, полагаясь на существующие у него представления (ожидания) по поводу поведения его партнера. Следовательно, в том случае, если эти ожидания окажутся верными, у него не возникнет желания изменить собственную линию поведения. Соответственно, равновесие по Нэшу будет представлять собой вероятностные оценки выбора строки(столбца), оказавшиеся верными (рациональными). Рассмотрим игру . Двое хотят встретиться . Расставаясь, они не оговорили точное место встречи, известно лишь, что встреча должна состояться либо в точке А, либо в точке В.
Предположим, что первый игрок полагает, что второй игрок выберет В в качестве места встречи с вероятностью 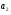 . В таком случае, ожидаемая полезность второго игрока от выбора им стратегии А: Eu1 (А)=100 (1- . В таком случае, ожидаемая полезность второго игрока от выбора им стратегии А: Eu1 (А)=100 (1-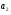 )+(0) )+(0) 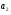 =100(1 - =100(1 - 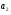 ) и ожидаемая полезность выбора В : Eu1(B)= ( 0 ) (1 - ) и ожидаемая полезность выбора В : Eu1(B)= ( 0 ) (1 -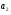 )+50 )+50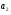 = 50 = 50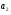
Игрок 1 может прибегнуть к использованию смешанной стратегии в том единственном случае, если Eu1(A) = Eu1 (B), т.е. полагая, что второй игрок будет выбирать B с вероятностью 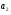 = 2/3 = 2/3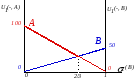 Рис.4.6.а Рис.4.6.аAналогично для второго игрока:
Игрок 2 может прибегнуть к использованию смешанной стратегии в том единственном случае, если Eu2(A)=Eu2(B), т.е. полагая, что первый игрок будет выбирать B с вероятностью 2/3. Дадим графическую иллюстрацию этой задачи, отложив по осям вероятности, к которыми каждый из игроков выбирает B в качестве места встречи.К сожалению, такого рода графическая иллюстрация может сопровождать лишь игры двух лиц, каждый из которых располагает двумя возможными стратегиями. Если первый игрок выберет B местом встречи с вероятностью менее 2/3, то второму игроку целесообразно направить свои шаги к A, если с вероятностью более 2/3- то целесообразно попытаться встретиться с первым игроком в B. И наоборот: если второй игрок выберет местом встречи B с вероятностью менее 2/3, то первому игроку следует направиться к A, а если - с вероятностью более 2/3 - то к B . Рис.4.6.б Профиль смешанных стратегий (1*,2*), соответствующий точке пересечения пунктирных линий, и будет равновесием по Нэшу в смешанных стратегиях, наряду с двумя равновесиями по Нэшу в чистых стратегиях(обратите внимание на черные точки на графике). Существенно, что неопределенность по поводу того, каким образом поведет себя партнер, отнюдь не означает неопределенности по поводу собственного поведения . При выборе первым игроком равновесной смешанной стратегии 1*(B)= 2/3 второй игрок оказывается безразличен между выбором любой из своих чистых стратегий, а следовательно, также и любой смешанной стратегий :Eu2(A,1*)=Eu2(B,1*)=U* 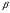 Eu2(B,1*)+(1- Eu2(B,1*)+(1- 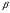 )Eu2(A,1*)=U* для )Eu2(A,1*)=U* для 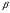 ≤1 ≤1 Логика довольно проста: если одна из чистых стратегий, входящих в состав смешанной имеет более высокий ожидаемый выигрыш(полезность), чем другие, то вероятность выбора это стратегии должна быть увеличена за счет снижения вероятности выбора стратегии менее выигрышной. Этот процесс продолжается до тех пор, пока не будет достигнуто равенство ожидаемого выигрыша по всем чистым стратегиям. Соответственно,таким же будет и ожидаемый выигрыш(полезность) любой смешанной стратегии. В приведенной игре самостоятельно проверьте безразличие игрока к выбору любой из чистых стратегий или выбору любой смешанной стратегии, включающей эти чистые стратегии, в предположении, что второй придерживается равновесной смешанной стратегии. Задачи: Найдите равновесие по Нэшу в смешанных стратегиях для следующих игр и дайте графическую иллюстрацию:
Именно равная полезность выбора любой стратегии, из числа входящих в состав смешанной равновесной стратегии или их произвольных комбинаций, не создающая для игрока стимулов придерживаться равновесной смешанной стратегии, вызывает, как правило, наибольшие сомнения в целесообразности рассмотрения равновесия Нэша в смешанных стратегиях: будучи индифферентным, партнер может легко отклониться от равновесной смешанной стратегии, что разрушает равновесие. Но как уже отмечалось, возможны несколько иные интерпретации смешанных стратегий, а именно, разумно предположить, что в игре участвует не один игрок, а множество игроков с одинаковыми функциями полезности, при этом часть из них избирает одну чистую стратегию, а часть - другую, что, в конечном счете, равноценно использованию смешанной стратегии одним игроком, тип которого неясен. Достижению равновесия способствуют: • Focalpoints. Достоверные равновесные исходы, обусловленные некими внешними обстоятельствами, влияющими на выбор. • Достижение некоего соглашения до начала игры(self-enforcingagreeement) • Для многократно повторяемых игр : стабильные социальные нормы (stablesocialconvention).Например: правила дорожного движения, допускающие пересечение перекрестка лишь при загорании зеленого света. • Равновесие по Нэшу как результат обучения или эволюции. Существование равновесия по Нэшу в смешанных стратегиях. Теорема Нэша. Теорема Нэша(Nash,1950): любая конечная некооперативная (бескоалиционная) игра имеет хотя бы одну ситуацию равновесия в смешанных стратегиях. Доказательство теоремы, основанное на использовании Brouwer's Fixed-Point Theorem, см Gibbons, c. 45- 48. Равновесие гарантированно существует в том случае, если а) множества чистых стратегий игроков сепарабельны и компактны ( непустое, выпуклое подмножество в евклидовом пространстве); б) функции полезности игроков- непрерывные и квазивогнутые . Однако невыполнение этих условий отнюдь не свидетельствует об отсутствия равновесий по Нэшу. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||