4 бескоалиционные(некооперативные) игры
 Скачать 261.08 Kb. Скачать 261.08 Kb.
|
|
Часть 2 ДИНАМИЧЕСКИЕ (МНОГОШАГОВЫЕ) ИГРЫ C ПОЛНОЙ ИНФОРМАЦИЕЙ. Экстенсивная форма представления игры. Дерево игры обычно изображается графически с помощью диаграммы , состоящей из конечного числа вершин. Вершины этой диаграммы называются явлются позициями(nodes). В каждой позиции делает ход один из игроков. Линии, соединяющие некоторую позицию с непосредственно следующими за ней, называются альтернативами этой позиции. Позиции, не имеющие последующих, называются окончательными(terminalnodes), а остальные - неокончательными(decisionnodes). На множестве окончательных вершин Т определены функции U1(t),U2(t), ... , Un (t), которые показывают сколько выиграет каждый игрок, если игра закончится в вершине t  Т. Т.Каждая окончательная вершина определяет единственную цепь , ведущую от начальной вершины к данному исходу. 2.1. ДИНАМИЧЕСКИЕ ИГРЫ С ПОЛНОЙ(COMPLETE) И СОВЕРШЕННОЙ(PERFECT) ИНФОРМАЦИЕЙ. В играх с совершенной информацией ранее сделанные ходы обозримы для всех игроков (как в дуополистических моделях Штакельберга и ценового лидерства). В играх, рассматриваемых в экономической литературе, как правило предполагается наличиеperfectrecall, т.е. игроки не забывают сделанные ими ходы, и, вообще, всю информацию, однажды ставшую им известной. Вернемся к рассмотрению игры MatchingPennies, полагая что игроки не одновременно, а последовательно выбирают ту или иную сторону монеты орел или решку, сообщая о своем выборе противнику. Различие между ходом и стратегией в динамической игре. Для одношаговых игр это различие несущественно(чистые стратегии совпадают с возможными ходами). Но его следует отчетливо осознавать, рассматривая динамические(многошаговые)игры. Ход (action): выбор орла(О) или решки(Р) Cтратегия - полный перечень действий игрока, которые следует предпринять при различных ситуациях , в которых игрок может оказаться Стратегии второго игрока:
У первого игрока в данном случае только две стратегии(О и Р). Если бы игру начинал второй игрок - все было бы наоборот.
Стратегия s3 для игрока 2- доминирующая МЕТОД ОБРАТНОЙ ИНДУКЦИИ(BACKWARDSINDUCTION) МОДЕЛЬ ТОРГА(BARGAINING GAME) РУБИНШТЕЙНА - СТИГЛИЦА(RUBINSTEIN-STIGLITZ) Рассмотрим последовательную игру Начнем анализ в рассмотрения последней стадии, в ходе которой(разумеется, если игра не будет окончена ранее, первый игрок выберет Т(3 > 0). Осознавая это, второй игрок ходом ранее несомненно выберет Т. Его выигрыш составит 1 , что предпочтительнее получения 0 на следующей стадии. Однако понимание того, каким будет предстояший выбор игрока 2, вынуждает игрока 1 закончить игру уже на первой стадии, что позволяет ему получить 2 вместо 1 . Решая подобные задачи методом обратной индукции, удобно рассматривать следующую последовательность ходов, постепенно отсекая последние этапы игры и перенося выигрыши, которые сулит игрокам их поведение на последующих этапах : Критика. Впрочем, предсказание исхода игры методом обратной индукции предполагает, как уже отмечалось, не просто рациональность игроков и не просто их осведомленность о рациональности партнера, а неч то большее- "commonknowledge" : " я знаю, что ты рационален; ты знаешь, что я знаю, что ты рационален; ты знаешь, что я знаю, что ты знаешь и т.д. и т.д.". При этом, чем более продолжительной является игра, чем более длинной становится приводимая "цепочка" рассуждений, тем менее убедительно они начинают выглядеть. Более того, заведомая выгодность продолжения игры для обоих партнеров, как в приведенной ниже сentipedegame (Rosenthal,1981) вызывает всё большие сомнения в исходе, предписываемом анализом игры методом обратной индукции, т.е. в выборе D на первом же этапе. При этом возникает естественное стремление оценить вероятность с которой игроки, осознавая свои выгоды от продолжения игры(чем дольше она длится, тем выше выигрыши), возможно будут выбирать А . сentipede game Вариант сentipede game (Tirole/ Fudenberg,pp.). 1 А1 2 А2 1 А3 2 А4 1 А5
Следуя логике обратной индукции первому игроку следует выбрать D1, застраховав себя от возможных потерь. Но в конечном итоге оба игрока могут существенно выиграть, продолжив игру, и все зависит от оценки поведения партнера: если игрок 2 полагает, что существует не менее чем 25 % шанс, что игрок 1 выберет А3, то он сыграет А2 , что делает осмысленным и ход А1 . Задачи: 1. Дайте нормальную(матричную) форму представления приведенной игры. 2.Играется следующая игра: партнер дает Вам $ 100. Вы можете взять эти деньги себе или же отдать их обратно первому игроку, добавив к ним еще $ 100 . Подобная передача денег ( с соответствующим добавлением $ 100) может быть повторена 5 раз. Как Вам следует поступить? 3. Для игры, дерево которой приведено ниже, определите, пользуясь методом обратной индукции, оптимальный ход первого игрока. Определите методом обратной индукции равновесные по Нэшу чистые стратегии всех трех игроков: Стратегия третьего игрока: если первый игрок выберет Т, если второй игрок выберет Т, выбрать ... если первый игрок выберет Т, если второй игрок выберет В, выбрать ... если первый игрок выберет В, выбрать ... Стратегия второго игрока: если первый игрок выберет Т, выбрать ... Стратегия первого игрока: выбрать ... Теорема Zermelo(Zermelo'sTheorem)(Zermelо,1913; Kuhn,1953) Любая конечная игра с совершенной информацией имеет равновесие по Нэшу в чистых стратегиях, которое может быть найдено методом обратной индукции. Более того, если игроки не имеют одинаковых выигрышей в различных окончательных позициях, методом обратной индукции возможно найти только одно единственное равновесие по Нэшу( что не исключает возможности существования прочихNEв чистых стратегиях) Доказательство - см.Mas- Colell A., Whinston M.D., Green J.R. Microeconomic Theory, с. 272-273 Экономические приложения: - модель дуополии Штакельберга( 1934 г) - Леонтьевская(1946 г.) модель взаимоотношений между фирмой и профсоюзом (монопольным поставщиком рабочей силы). Модель торга(bargaininggame) Рубинштейна - Стиглица(Rubinstein-Stiglitz) Пример простейшей модели торга:
Обратите внимание, что если а =1, b< 1, все достанется А. Иногда в такого рода моделях задается иное более общее правило раздела средств между игроками на последней стадии игры , а именно - оговорено, что в том случае, если игроки не смогут договориться между собой, эти средства будут поделены между ними в некоей изначально заданной пропорции. Разумеется, с тем чтобы стимулировать заключение соглашения между сторонами, это правило предполагает своего рода штраф: не достигнув компромисса, стороны смогут неким образом разделить между собой лишь оговоренную часть первоначальной суммы. Рассмотренная здесь модель есть частный случай этой более общей постановки, предполагающая , что участники наказываются изъятием всего объекта, подлежавшего разделу. Задача: 1.(модификация рассмотренной выше задачи)Определите, какую часть доллара должен предложить первый игрок второму в первый день, с тем, чтобы он принял это предложение сразу же, если известно, что в случае, если соглашение не будет достигнуто, на третий день каждый получит по 40 центов. 2.Игроки А и В делят между собой 131 тыс рублей. Процентная ставка для А- 10%, для В - 5 % в день. В первый день В делает предложение А. Если оно отклоняется, то во второй день предложение о пропорциях раздела делает А. В случае отказа В от предложения А, инициатива вновь переходит к В, и он делает последнее предложение А. Если в течение 3-х дней договоренности так и не удалось достичь, в четвертый день А достается 121 тыс руб, а В - 10 тыс руб. Определите, какую часть доллара должен предложить игрок А игроку В в первый день, с тем чтобы он согласился на него. 2(а)Определите, какую часть доллара должен предложить игрок А игроку В в первый день, с тем чтобы он согласился на него, если во второй день игрок А может сделать повторное предложение игроку В, а в третий день инициатива переходит к игроку В. 2(б)Определите, какую часть доллара должен предложить игрок В игроку А в первый день, с тем чтобы он согласился на него, если в первый день он делает предложение игроку А(а в дальнейшем они чередуются). Модель Рубинштейна в общем виде: Делится 1 доллар или 1 пирог Дисконт 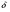 - единый - единыйПредложения делаются до тех пор пока одно из них не будет принято. Если договоренность не будет достигнута, оба игрока ничего не получают.
(2++ -2) = T =0T =(2) при T Этот результат можно получить и более простым путем(см Тироль Рынки и рыночная власть).Игрок, делающий предложение, претендует на получение Vi, а игрок, которому делается предложение,на получение Wi. V i + W i =1 Когда игрок 1 делает предложение W2 = V2 Когда игрок 2 делает предложение W1 = V1 Т.к. игра симметрична: V1 = V2 = V ; W1 = W2 = W Решив систему W= V V+ W=1 получаем: V = 1/ (1+); W=/(1+) Итак, при Т игрок , делающий предложение, претендует на получение доли равной 1/ (1+), при этом второму игроку достается доля, равная /(1+). Равновесные стратегии состоят в принятии долей, больших или равных /(1+) , и отклонении меньших. Рубинштейн ( в некоторых переводных изданиях называемый Рубинстайном) (Rubinstein) доказал, что это равновесие бесконечного горизонта единственно. Экономическое приложение: торг предпринимателей с профсоюзами. 2.2 СОВЕРШЕННЫЕ РАВНОВЕСИЯ ПО НЭШУ (SPNE - SUBGAMEPERFECTNASHEQUILIBRIUM ) ДЛЯ ИГР С СОВЕРШЕННОЙ ИНФОРМАЦИЕЙ. УСЕЧЕНИЕ ИГРЫ(SUBGAME). НЕОБОСНОВАННЫЕ УГРОЗЫ(INCREDIBLETHREATS). В динамических играх, так же как и в играх статических, остро стоит проблема выбора из равновесий по Нэшу тех из них, которые представляются более "reasonable", т.е. более разумными. Такого роды равновесия, впервые выделенные R. Selten в 1965 году, получили названиe совершенных равновесий по Нэшу (subgameperfectNashequilibrium - SPNE). Ведем необходимые определения. Def. "Усечение игры" или "усеченная игра"(subgame) Gsпредставляет собой меньшую игру в пределах большой исходной игры G, которая начинается в одной из неокончательных определенных позиций(decisionnodes) и включает все неокончательные и окончательные позиции, следующие вслед за начальной для данной игры позицией. Иначе говоря, начав играть в усечении игры Gs, партнеры продожают делать это до конца игры G. Для игр с совершенной информацией - любая из "ветвей" дерева игры G. Def. (Selten, 1965): равновесное по Нэшу сочетание стратегий игроков (NEequilibrium) обладает свойством совершенства (т.е. является subgameperfectNashequilibrium - SPNE) , если она одновременно является равновесной по Нэшу для всех усечений (subgames) Gsисходной игры G. Пример 1. Рассмотрим проблему вхождения фирмы в отрасль, монополизированную другой фирмой. Монополия может смириться с вхождением на рынок новой фирмы, оставив цену на прежнем уровне(высокая - Н), но может и временно снизить ее , чтобы отпугнуть конкурента. В зависимости от того, как она себя поведет, он, в свою очередь, решает для себя вопрос о целесообразности вхождения в отрасль. Используя метод обратной индукции, найдем равновесный по Нэшу исход этой игры (a1 *, R2(aM*)) =(низкая; не входить), где R2(a1*) - реакция конкурента на оптимальное решение монополии aM*, т.е. снижение цены. С тем, чтобы сформулировать стратегии игрока 2 и выделить все равновесные сочетания стратегий игроков, целесообразно перейти от экстенсивной к нормальной форме представления этой игры: стратегии игрока 1(монополии):{ цена высокая; цена низкая} стратегии игрока 2 (конкурента): 1- не входить,если цена низкая; входить, если высокая . 2- никогда не входить (т.е.не входить,если цена низкая; не входить, если цена высокая) 3- входить всегда (т.е. входить,если цена низкая; входить, если высокая) 4- не входить, если цена высокая; входить, если низкая
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
