4 бескоалиционные(некооперативные) игры
 Скачать 261.08 Kb.
|
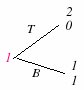                               ТЕМА 4 БЕСКОАЛИЦИОННЫЕ(НЕКООПЕРАТИВНЫЕ) ИГРЫ. БЕСКОАЛИЦИОННЫЕ(НЕКООПЕРАТИВНЫЕ) ИГРЫ С ПОЛНОЙ (СOMPLETE)ИНФОРМАЦИЕЙ.
Дополн. итература: MIT 14.12 Economic Applications of Game Theoryhttp://ocw.mit.edu/OcwWeb/Economics/14-12Fall-2005/CourseHome/index.htm Lecture Notes This section contains documents that could not be made accessible to screen reader software. A "#" symbol is used to denote such documents. Below is a selection of lecture notes and recitation notes that approximate chronologically the topics and themes listed on the calendar.
РАЗЛИЧНЫЕ ТИПЫ ИГР.
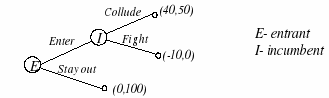
Игрой называется система G= {I; S1,S2 , ..., Sn; U1,U2, ...,Un } I- множество игроков; Si - множество чистых стратегий i-го игрока (Si =(si1, si2, si3, ..., sik )) Ui- функция выигрыша i-го игрока. Стратегическая форма представления игры (платежная матрица или матрица выигрышей) Пример: бросание монеты (MatchingPennies)
Статические игры 1.1 CМЕШАННЫЕ СТРАТЕГИИ. Если бы во внешнем мире отсутствовала бы неопределенность, то возможно было бы выработать некую чистую стратегию, в наибольшей степени соответствующую складывающейся ситуации (например, купить акции именно той компании, которой уготован наибольший успех, или выбрать специальность, которая окажется наиболее востребованной на рынке в будущем). Но подобный точный прогноз невозможен: игрок не в состоянии предугадать "состояние мира " и предсказать заранее реакцию партнеров по игре(например, тех, кто стоит перед аналогичным выбором ) и пр. Кстати говоря, выпадающее "состояние мира" также может быть рассмотрено как результат действия игрока –«Природа» (Nature). В некоторых ситуациях непредсказуемость действий партнеров по игре(включая "природу") искупается тем, что существуют так называемые доминирующие стратегии, т.е. стратегии наиболее предпочтительные вне зависимости от поведения прочих игроков. Впрочем, существование доминирующих стратегий, т.е. полная независимость выбора от поведения прочих игроков, встречается нечасто, и, как прав ило, игрок все же выигрывает от повышения степени своей информированности, подобно вратарю, знающему в какую часть ворот будет пробит пенальти. Сталкиваясь с неопределенностью, игрок, выбирая собственную стратегию, опирается на имеющееся у него представление о вероятностях, с которыми его партнеры будут избирать ту или иную стратегию, т.е. приписывает некие субъективные вероятности (subjectiveprobabilities) возможным стратегиям поведения партнеров по игре. С учетом этих вероятностей индивид и выбирает чистую стратегию, обеспечивающую ему получение наивысшей ожидаемой полезности. Но могут ли индивиды отклоняться от некоторой заданной линии поведения(чистой стратегии) прибегая к использованию смешанных стратегий, и что может служить объяснением такого рода отклонений ? Впрочем, следует вначале дать определение смешанной стратегии. Def. При данном (конечном) множестве чистых стратегий i-го игрока Siсмешанная стратегия 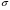 i представляет собой вероятностное распределение, приписывающее каждой чистой стратегии i - го игрока sikSi , k=1,...K, вероятность  ≥ 0, k= 1. Чистая стратегия может рассматриваться как частный случай смешанной стратегии, в которой одной из чистых стратегий приписана вероятность 1.
Смешанные стратегии игроков 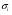 можно рассматривать как задаваемые своими барицентрическими координатами точки ( k -1)-мерного симплекса(рис.4.1.).Рис.4.1. Возвращаясь к интерпретациям смешанных стратегий, следует указать как на возможность того, что , прибегая к смешанным стратегиям, игрок повышает свой выигрыш за счет понижения степени предсказуемости своего поведения. Но такого рода объяснение уместно лишь в повторяющихся динамических играх. Если же говорить о играх статических, то возможно указать на две причины, обусловливающие целесообразность рассмотрения смешанных стратегий. Во-первых, использование смешанных стратегий( например, диверсификация портфеля ценных бумаг) может иметь преимущества перед использованием чистых стратегий( вложением средств в акции лишь одной из фирм). Вспомним пример, упомянутый ранее. Доходность акций первой фирмы составляет 20 % в первом и 10% - во втором состоянии( будем полагать их равновероятными) и наоборот.
Поровну распределив исходные средства ( 100 долл) между покупкой этих акций, инвестор обеспечит себе гарантированное получение 15% дохода. В подобном случае полезность u(E(W)) будет выше, чем ожидаемая полезность выбора любой из чистых стратегий Eu. Во-вторых, смешанные стратегии упрощают рассмотрение ситуаций асимметричной информации. Например, часть игроков всегда выбирают одну чистую стратегию, а оставшаяся часть - другую чистую стратегию(например, одни всегда тщательно запирают машины, а другие - нет). Не будучи в состоянии различить, к какой из этих подгрупп принадлежит агент, вступающий в игру(например, обращающийся за страховкой), его партнер по игре будет предполагать, что он имеет дело с неким игроком, прибегающим к смешанной стратегии( вероятности использования чистых стратегий которым будут определяться относительной численностью подгрупп). 1.2. СТРАТЕГИИ ДОМИНИРУЮЩИЕ И ДОМИНИРУЕМЫЕ. Обозначим S-i множество стратегий всех игроков за исключением i- го игрока. Def. Доминирующейстратегией i- го игроканазывается стратегия 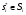 , обеспечивающая игроку наибольший выигрыш(полезность) вне зависимости от выбора, , который делают его партнеры по игре, т.е.U ( si*, s-i) ≥ U( si, s-i) для любых 
Графически доминирующая стратегия может иллюстрироваться двояким образом. На рисунке 4.2.а вертикальным осям, каждая из которых соответствует той или иной чистой стратегии противника(второго игрока), откладываются все возможные выигрыши первого игрока. Каждой чистой стратегии первого игрока соотвествует некий набор точек(по одной на каждой из вертикальных осей). Доминирующей же стратегии соответствует набор точек, занимающих наивысшие позиции на каждой из осей ( или прямая линия, проходящая выше линий, соответствующих прочим чистым стратегиям).
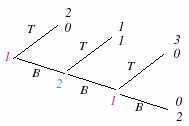
Иначе те же вертикальные оси можно полагать осями n- мерного пространства (где n- количество чистых стратегий второго игрока). Тогда каждой чистой стратегии первого игрока будет соответствовать некая точка этого пространства(рис.4.2.б), адоминирующую стратегию можно представить как точку лежащую северо-восточнее всех прочих точек. Строго доминирующие стратегии могут существовать у обоих игроков, (в нашем примере - это стратегии В иR). В подобных случаях наблюдается равновесие в доминирующих стратегиях, предполагающее полную независимость игроков друг от друга. При наличии у игрока доминирующей стратегии все прочие его стратегии стратегии являются доминируемыми и могут быть отброшены. Подобное элиминирование доминируемых стратегий, разумеется, возможно не только при наличии у игрока доминирующей статегии. Некоторые стратегии, не являясь доминирующими(т.е. абсолютно предпочительными), могут в то же время быть относительно предпочтительней части других , так называемых доминируемых стратегий. Рассмотрим новую игру, отличающуюся от предыдущей лишь добавлением третьей статегии (М) первого игрока . В этой игре отсутствую доминирующие стратегии, но стратегия В по-прежнему доминирует стратегию T.
Строго доминируемые стратегии имеют строго меньшие значения выигрыша(полезности) по всем возможным стратегиям партнеров s-i, чем некая иная стратегия или стратегии этого игрока, а слабо доминируемые - значения равные и меньшие(хотя бы для одного s-i). Иначе говоря: Def.1 Стратегия i-го игрока  в игре G является строго доминируемой, если существует иная стратегия 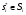, такая, что для всех U ( si*, s-i) ≥ U ( si, s-i), т.е. при любых обстоятельствах есть другая стратегия - более предпочтительная. Строго доминируемые стратегии следует вычеркнуть из игры, упростив ее структуру. При этом вычеркивание одной из чистых доминируемых стратегий одного игрока, часто позволяет избавиться и от части чистых стратегий другого игрока. Рассмотрим следующую игру:
Среди стратегий игрока Aнет доминируемых стратегий, лишь стратегия b4 второго игрока доминируется стратегией b3. Но элиминирование стратегии b4 позволяет избавиться от стратегии а1( после вычеркивания последнего столбца, содержащего высокий выигрыш именно в первой строке) она начинает доминироваться стратегией а2. Вычеркивание первой строки устраняет возможность нулевого выигрыша при выборе b2 , и эта стратегия начинает доминировать b2 и т.д(продолжите сами). Однако следует подчеркнуть, что для элиминирования строго доминируемых стратегий недостаточно простого предположения о рациональности игроков. Необходимо предположить нечто большее: • игрок Aзнает, что игрок В рационален ( и не выберет b4), • игрок В знает, что игрок Aзнает, что игрок В рационален ( и, соответственно, игрок A никогда не выберет а1), • игрок А знает, что игрок В знает, что игрок А рационален и т.д. Подобное предположение нетождественно обычной рациональности, а представяет собой нечто большее - так называемое "общее знание" - commonknowledge). Длина цепочки зависит от количества последовательных шагов по элиминированию стратегий, чем она длинее - тем большие сомнения начинает порождать принятие подобной предпосылки. Допустимость последовательного элиминирования доминируемых стратегий становится тем более сомнительным, если речь идет о элиминировании слабо доминируемых стратегий. Дело в том, что эта процедура может значительно изменить стратегическую природу игры, поскольку конечный результат в некоторых случаях находится в непосредственной зависимости от от порядка (последовательности) элиминирования слабо доминируемых стратегий. Пример:
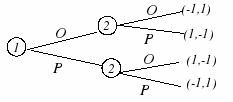
Дальнейшее уточнение определения доминируемой стратегии обусловлено учетом того обстоятельства, что при определенных ситуациях стратегия siможет доминироваться одной стратегией , а при других - другой. Например: если игрок 2 будет выбирать L , то игроку 1 выгоднее выбрать T, а если игрок 2 предпочтет сыграть R, то игроку 1 следует играть B | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||