4 бескоалиционные(некооперативные) игры
 Скачать 261.08 Kb.
|
|
4, но обрек себя на получение только 1в каждой из последующих игр, то приведенная стоимость его выигрышей(начиная с "момента предательства", к нему и будут приводится последующие выигрыши) равна PV = 4 + (1/ r). Придерживаясь стратегии сотрудничества, игрок получал бы PV= 3 + (3/ r). 3 + (3 / r) > 4 + (1/ r). Итак, выгоды от кооперации превосходят выгоды "предательской" политики, если r < 2,00 (для дисконт-фактора : 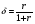 >1/3). Итак, при уровне дисконта близком к единице (едином с силу симметричности выигрышей) стратегия наказания формирует равновесие по Нэшу, ведущее к кооперации - у обеих сторон отсутствует заинтересованность в отклонении от сотрудничества. Но коль скоро одна из сторон все же отклонилась от сотрудничества, ей ничего не остается как выбирать в каждой последующей игре некооперативное действие, ибо попытки продемонстрировать вновь свою приверженность разрушенному союзу являются и напрасными(она не может рассчитывать на прощение, если партнер придерживается стратегии курка) и обременительными для нее. Но в определенном смысле, это наказание - слишком жестоко и лишает партнеров выгод от взаимного воспитания в духе сотрудничества(хотя несомненно это сотрудничество стимулирует). Более того, пара равновесных по Нэшу стратегий курка формирует в то же самое время и совершенное равновесие по Нэшу. Для того, чтобы проверить, удовлетворяет ли требованиям subgameperfectNashequilibriumстратегия курка( triggerstrategy), точнее пара таких стратегий, следует убедиться в том, что эта пара стратегий будет равновесной не только для игры в целом, но и для каждого усечения этой игры. Для игр с конечным числом повторений Т :усечение игры( subgame), начинающееся на ходе t +1, обозначают G(Т - t).Таких усечений может быть множество, в зависимости от числа вариантов развития событий до моментаt . Для игр с бесконечным числом повторений : усечение игры( subgame), начинающееся на ходе t +1, идентична игре в целом. В сущности возможны только два вида усечений бесконечно повторяемой игры: начинающиеся с составной игры, в которой партнеры кооперируются ( а следовательно, кооперировались и до того) и те, началу которых предшествовало предательство одной из сторон. В первом случае, следуя стратегии курка выгоднее продолжать сотрудничество, во втором - на него нельзя рассчитывать и остается предпринимать действия, предписываемые для такого рода ситуаций все той же стратегией курка. 3. Стратегия "Око за око..."( Tit-for-tat strategy )
Таким образом эта стратегия - повторение последнего хода партнера допускает возврат к сотрудничеству с раскаявшимся партнером Но в то же время в отличие от стратегии курка стратегия tit-for-tat не ведет к устойчивому сотрудничеству(не является совершенным по Нэшу): партнер, оказавшись в сложном положении, вновь предаст, рассчитывая, на возврат к сотрудничеству в будущем. Поскольку выигрыш предающего первым имеет большую приведенную стоимость, чем полее поздний во времени выигрыш второго игрока в момент возврата первого к сотрудничеству, то целесообразно рассматривать варианты этой стратегии, предполагающие своего рода штрафы за предательство. Например, игрок может допускать возврат к сотрудничеству, но лишь после того, как партнер дважды продемонстрировал свое стремление кооперироваться и, соответственно, этот игрок дважды получил высокие платежи(4). Дисконт 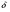 может интерпретироваться несколько шире чем обычно, если речь идет об играх с неизвестным числом повторений. Будем полагать, что в конце каждой игры определяется, будет ли играться следующая. Например бросается кубик, и при выпадении "шестерки" игра прекращается. В этом случае р ( вероятность прекращения игры) равна 1/ 6. Соответственно, вероятность ее продолжения (1- р) =  . Эту вероятность следует учесть, рассчитывая ожидаемый выигрыш от продолжения игры. В этом случае 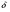' одновременно учитывает как разновременность выигрышей, так и возможность прекращения игры.Чем ниже дисконт (и чем выше процентная ставка), тем меньше значит будущее ( и тем выше соблазн нарушить соглашение), неопределенное будущее значит еще меньше, и соблазн повести cебя некооперативно возрастает: если раньше условием сохранения кооперации было условие  ), то теперь эти пороговые значения должны сместиться (дисконт 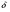должен повыситься: ,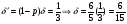а процентная ставка, соответственно, сократиться).
| |||||||||||||||||