4 Расчёт закрытой зубчатой конической передачи

• Название: 4 Расчёт закрытой зубчатой конической передачи
• Анкор: 4 Расчёт закрытой зубчатой конической передачи.doc
• Дата: 07.09.2018
• Размер: 281 Kb.
• Имя файла: 4 Расчёт закрытой зубчатой конической передачи.doc
• Тип: Документы; #24219

4 Расчёт закрытой зубчатой конической передачи
Расчет зубчатых передач производится в соответствии с ГОСТ 21354-75. Основными видами расчетов является расчеты на контактную выносливость активных поверхностей зубьев и расчет зубьев на выносливость при изгибе.
4.1 Выбор материала зубчатых колес и определение допускаемых напряжений
Зубчатые колеса редукторов в большинстве случаев изготавливают из углеродистой стали. При выборе марок стали учитывают назначение и тип передачи, требования к габаритам и массе, технологию изготовления, экономическую целесообразность.

Примем для шестерни и колеса материал одной марки, а различную твердость обеспечим различной термообработкой. Примем сталь 40Х с твердостью 200-230 HB.

Допускаемое контактное напряжение для каждого из зубчатых колёс определяется по формуле (3.1) [2, с.28]:

,МПа (4.1)

где S_H ─ коэффициент запаса прочности;

Z_R ─ коэффициент, учитывающий шероховатость поверхности зубьев;

Z_V ─ коэффициент, учитывающий окружную скорость;

K_L ─ коэффициент, учитывающий влияние смазки;

K_ХН ─ коэффициент, учитывающий размер зубчатого колеса.

S_H =1,1 ─ по [2,с.29] табл. 3.1;

Z_R ·Z_V ·K_L ·K_ХН=0,9 ─ принимают при проектировочных расчётах по ГОСТ 21354 .

σ_Нlim –предел контактной выносливости поверхности зубьев, МПа, определяется по формуле [2, с.28]:

,МПа (4.2)

где K_HL ─ коэффициент долговечности;

K_HL =1 ─ по [2, с.28];

σ_Нlimb – предел контактной выносливости поверхности зубьев, который зависит от твердости материала шестерни (колеса) и вычисляется по


у

формуле ([2, с.31] табл. 3.2):

,МПа; (4.3)

где НВ – твердость материала по Брюннелю.

В данном проекте исходным материалом шестерни (колеса) является сталь 40Х (термообработка – улучшение) с твердостью материала по Брюннелю НВ=180 – 350 ─ по [2, с.31] табл.3.2.

;

;

;

.





Принимаем для проектировочного расчёта в качестве допускаемого напряжения [σ_Н]=[σ_Н2]=384,5 МПа.

Определяем допускаемое напряжение на выносливость зубьев при изгибе [σ_F],МПа, определяем раздельно для шестерни и колеса по формуле (3.2) [2, с.32]:

(4.4)

где σ_Flim – предел выносливости зубьев при изгибе, соответствующий эквивалентному числу циклов перемены напряжений, МПа, рассчитываем по формуле:

(4.5)

где σ_Flimb  предел выносливости зубьев при изгибе, соответствующий базовому числу циклов перемены напряжений, МПа;

K_Fα  коэффициент, учитывающий влияние шлифования переходной поверхности зуба;

K_Fd коэффициент, учитывающий влияние деформационного упрочнения или электрохимической обработки переходной поверхности зубьев;

K_Fo коэффициент, учитывающий влияние двухстороннего приложения нагрузки;

K_FL коэффициент долговечности.

σ_Flimb1 = 414 МПа, σ_Flimb2 = 360МПа  по [2, с.31] табл. (3.2) для шестерни и колеса в зависимости от способа термической и химико-термической обработки;K_Fα=1  для зубьев с нешлифованной поверхностью; K_Fd =1при изготовлении колёс без данных видов обработки; K_Fo =1при одностороннем приложении нагрузки; K_FL =1для длительно работающих передач.

;

.

S_F – коэффициент безопасности, определяем по формуле [2, c.32]:

, (4.6)

где S_F^’  коэффициент, учитывающий нестабильность свойств материала зубчатого колеса и ответственность зубчатой передачи;

S_F^”  коэффициент, учитывающий способ получения заготовки зубчатого колеса.
S_F^’ =1,75; S_F^”=1  по [2, с.29] табл. 3.1.



YSкоэффициент, учитывающий градиент напряжения и чувствительность материала к концентрации напряжений;

YRкоэффициент, учитывающий шероховатость переходной поверхности;

KXF коэффициент, учитывающий размеры зубчатого колеса.

σ_Flimb1 = 414 МПа, σ_Flimb2 = 360МПа  по расчётам;S_F=1,75; Y_S =1по [2, с.33] рис. 3.1;Y_R=1; KXF=1.

;

.

4.2 Проектировочный расчет закрытой зубчатой передачи
Так как основной причиной выхода из строя зубьев закрытых передач, работающих при обильной смазке, является усталостное контактное выкрашивание, то проектный расчёт закрытых передач выполняется на контактную выносливость, а затем после уточнения параметров передачи , проверяют действительное контактное напряжение и сравнивают их с допускаемыми с последующей проверкой зубьев на выносливость при изгибе.

При проектировочном расчете определяют предварительное значение среднего делительного диаметра шестерни по формуле (4.1) [2, с.46]: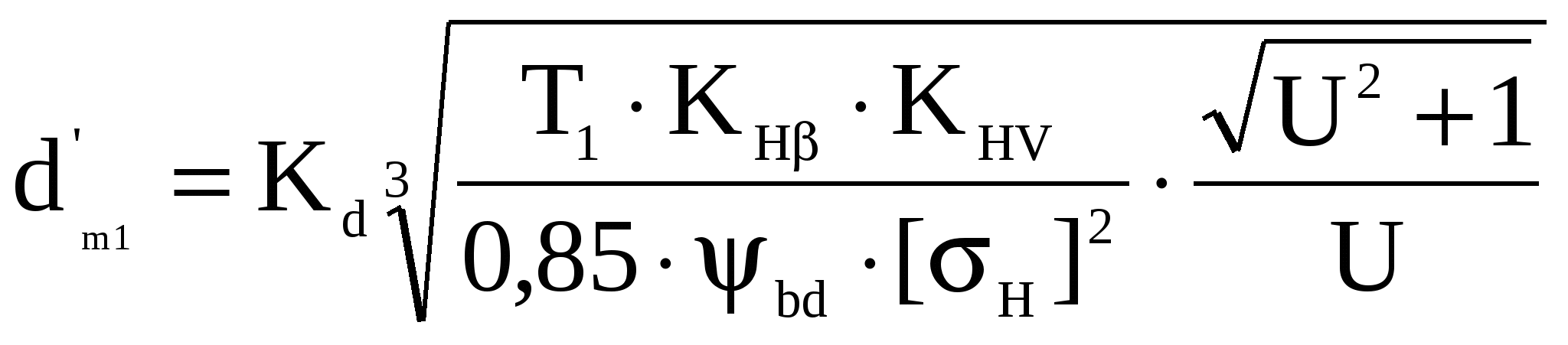

,мм (4.7)

где K_d  вспомогательный коэффициент, МПа;

ψ_bd  коэффициент ширины зубчатого венца шестерни относительно её среднего делительного диаметра;

K_H  коэффициент, учитывающий неравномерность нагрузки по ширине венца;

K_HV  коэффициент, внешней динамической нагрузки.

K_d =770 МПа ─ для прямозубых передач [2, с.46];Т₁=46 Н·м ─ по расчётам (табл. 2.1); ψ_bd=0,5 ─ по [2, с.46]; K_H =1,25 ─ по графику [2, с.35] рис. 3.2; K_HV =1,25 ─ по [2, с.34] табл. 3.3; U=3,2 ─ по расчётам; [σ_Н]=384,5 МПа ─ по расчётам.



Определяем ширину венца шестерни по формуле:

b₁ _bdd^’_m1, мм (4.8)

b₁ 0,581,7941 мм.

Определяем угол делительного конуса:

δ₁^’=arctg(1/U) (4.9)

δ₁^’=arctg(1/3,2)=17,4º

Определяем внешнее конусное расстояние:

. (4.10)

При этом необходимо выполнение условия (b/R≤0,3).

;

b/R=41/157,25=0,26;

0,26≤0,3 ─ условие выполняется.

Определяем внешний делительный диаметр шестерни:

(4.11)

.

Предварительно принимаем Z₁ =17 и определяем внешний окружной модуль зацепления:

m^’_te=d^’_e1/z^’₁,мм; (4.12)

m^’_te=94,05/17=5,5 мм.

Округляем m^’_te до стандартного m_n в соответствии с [2,с.36] табл.3.5:

m_te= m_n=6 мм, при выполнении условия m_te ≥(1/8─1/10)b:

(1/8─1/10)b=(5,1─4,1);

6≥(5,1─4,1) ─ условие выполняется.

Определяем число зубьев шестерни:

Z1= d_e1 /m_te ; (4.13)

Z1= 94,05 /6=16;

Z₂=Z₁·U; (4.14)

Z₂=16·3,2=52.

Уточняем истинное передаточное число:

U= Z₂/Z1 (4.15)

U= 52/16=3,25.

Отклонение U от заданного значения не должно превышать ±3٪, в нашем случае это условие соблюдается.

Действительные величины углов делительных конусов:

δ₁=arctg(Z1/ Z₂); (4.16)

δ₂=arctg(Z2/ Z₁). (4.17)

δ₁=arctg(16/ 52)=17,1º;

δ₂=arctg(52/16)=72,9º.

Действительное внешнее конусное расстояние:

. (4.18)

.

Средний модуль зацепления:

(4.19)



Определяем средний делительный диаметр окружности шестерни и колеса:

d_m1Z1m_m; (4.20)

d_m2Z2m_m. (4.21)

d_m1165,25=84мм;

d_m2=525,25=273мм.

Определяем условное межосевое расстояние:

(4.22)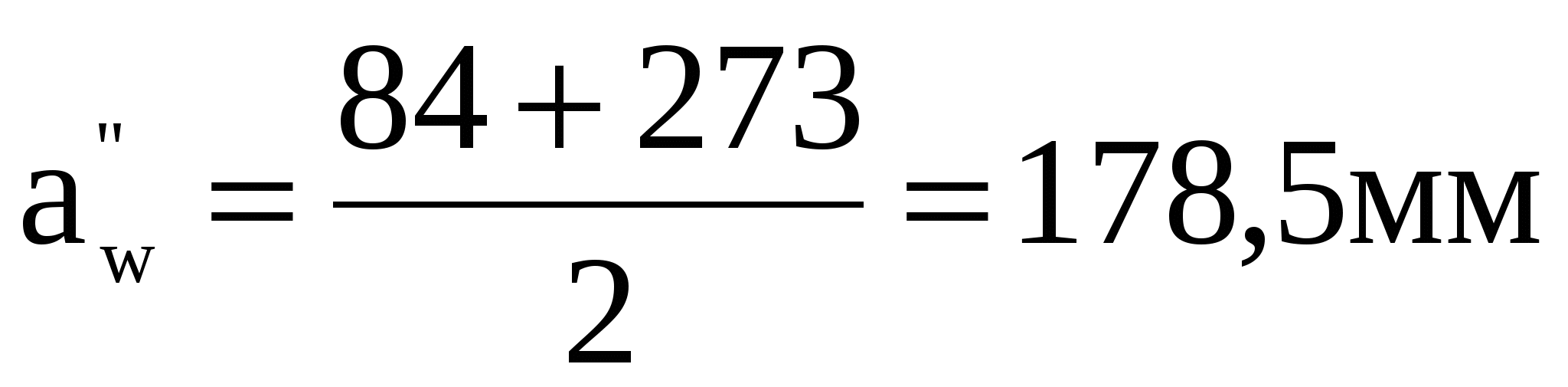

.

4.3 Проверочный расчет зубьев по контактным напряжениям

Определяем окружную силу в зацеплении :

,Н (4.23)

где Т₁=46000Н·мм ─ по расчётам табл.(2.1).



Определяем окружную скорость колёс:

(4.24)

где n₁=1208 мин^-1 ─ по расчётам табл.(2.1).


Выбираем степень точности передачи [2,с.38] табл.3.6: 8-я степень точности.

Расчетные контактные напряжения в полюсе зацепления определяются по формуле по формуле (4.2) [2, с.48]

(4.25)

где Z_H  коэффициент учитывающий форму сопряженных поверхностей зубьев;

Z_m  коэффициент учитывающий механические свойства материала сопряженных зубчатых колёс;

Z_е  коэффициент учитывающий суммарною длину контактных линий;

W_Ht- удельная расчетная окружная сила, Н/мм.

Удельная окружная динамическая сила:

,Н/мм (4.26)

где δ_Н ─ коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля зуба на динамическую нагрузку;

g₀ ─ коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса.

δ_Н = 0,06 ─ по [2,с.49] табл. 4.2; g₀ = 5,3 ─ по [2,с.49] табл. 4.3; V=5,31 м/с; а^”_w=178,5 мм; U=3,25.



Удельная расчетная окружная сила в зоне её наибольшей концентрации:

,Н/мм; (4.27)

где F_t=1095,2H; K_Hβ=1,25; b=41мм.

.

Коэффициент, учитывающий динамическую нагрузку в зацеплении:

; (4.28)



Удельная расчетная окружная сила:

(4.29)

где K_Hβ=1,25; K_Hν=1,25; K_A=1,01.

.

Z_H =1,77 ;Z_m =275; Z_е =0,9 ─ по [2,с.48];W_Ht=57,18H/мм; d_m1=84мм; U=3,25.



Полученная величина контактных напряжений не превышает величину допускаемых контактных напряжений более чем на 5٪.

4.4 Проверочный расчет зубьев по усталостным напряжениям изгиба

Расчетное напряжение изгиба зубьев σ_F ,МПа определяют по формуле [2, с.50]:

(4.30)

где Fкоэффициент, учитывающий форму зуба;

E коэффициент, учитывающий перекрытие зубьев;

 коэффициент, учитывающий наклон зуба;

W_Ft удельная расчетная окружная сила при изгибе H.

Определим для какого элемента пары «шестерня-колесо» будем проводить расчёт. Для этого определим у которого меньшая величина отношения [σ_F1(2)]/Y_F1(2) :

[σ_F1]/Y_F1 =236,57/4,3=55,02;

[σ_F2]/Y_F2 =205,71/3,72=55,30.

Таким образом расчёт будем проводить для шестерни.

Удельная окружная динамическая сила:
,Н/мм (4.31)

где δ_F ─ коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля зуба на динамическую нагрузку.

δ_F = 0,16 ─ по [2,с.49] табл. 4.2; g₀ = 5,3 ─ по [2,с.49] табл. 4.3; V=5,31 м/с; а^”_w=178,5 мм; U=3,25.

Н/мм.

Удельная расчетная окружная сила в зоне её наибольшей концентрации:

,Н/мм; (4.32)

где K_F  коэффициент, учитывающий неравномерность нагрузки по ширине венца;

F_t=1095,2H; K_F =1,52 ─ по графику [2, с.35] рис. 3.2; b=41мм.

;

Коэффициент, учитывающий динамическую нагрузку в зацеплении:

; (4.33)



Удельная расчетная окружная сила при изгибе:

(4.34)
где K_Fβ=1,52; K_Fν=1,25; K_A=1,45.
.


4.5 Параметры зубчатых колес
Конструкция кованого колеса приведена на рисунке 4.1.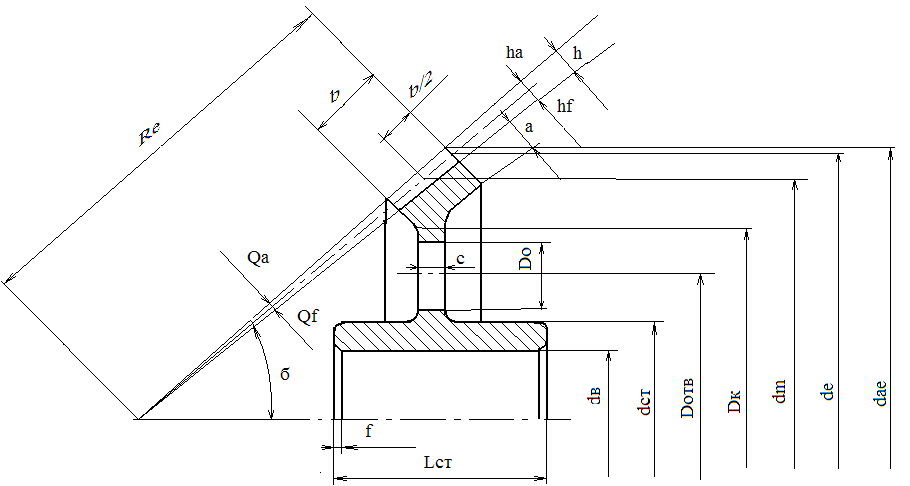

Рисунок 4.1 – Конструкция и основные геометрические параметры конического колеса

1. 
   Количество зубьев Z:
   

Z₁=16;

Z₂=52.

2. 
   Угол делительного конуса δ :
   

шестерни δ₁=17,1 º

колеса δ₂=90- δ₁=72,9º

3. 
   Внешний окружной модуль m_te :
   

m_te =6 мм.

4. 
   Внешнее конусное расстояние R_e:
   

R_e =163,22мм

5. 
   Среднее конусное расстояние R_m:
   

R_m =R_e -0,5b=163,22-0,5·41=142,72мм

6. 
   Средний модуль зацепления m_m :.
   

m_m =5,25 мм.

7. 
   Средний делительный диаметр d_m:
   

d_m1=84мм;

d_m2=273мм.

8. 
   Радиальный зазор в зацеплении С:
   

С=0,2· m_te =0,2·мм.

9. 
   Внешняя высота головки зуба h_ae :
   

h_ae=m_te=6 мм.

10. 
    Внешняя высота ножки зуба h_fе:
    

h_fе= h_ae+С=6+1=7мм.

11. 
    Внешняя высота зуба h_е :
    

h_е= h_ae+ h_fе =6+7=13мм

12. 
    Внешний делительный диаметр окружности d_е:
    

d_е1Z1m_te=16·6=96мм;

d_е2Z2m_te=52·6=312мм.

13. 
    Внешний диаметр окружности вершин зубьев d_ае :
    

d_ае1=d_е1+2 h_ae cosδ₁=90+26·cos17,1=111,29мм;

d_ае2=d_е2+2 h_ae cosδ₂=312+26·cos72,9=315,53мм.

14. 
    Внешний диаметр окружности впадин зубьев d_fе :
    

d_fе1=d_е1-2,4 h_ae cosδ₁=90-2,46·cos17,1=82,24мм;

d_fе2=d_е2-2,4 h_ae cosδ₂=312-2,46·cos72,9=307,77мм.

15. 
    Толщина обода a:
    

a=(2,0-4,0)  h_ae =36=18 мм.

16. 
    Диаметр ступицы
    

d_cт=(1,6-1,8)d_вала;

d_вала1=40 мм;

d_вала2=45 мм;

d_cт1=1,7·40=68мм;

d_cт2=1,7·45=76,5мм;

17. 
    Длина ступицы
    

l_cт=(1,2-1,8)d_вала

l_cт1=1,4 40=56мм

l_cт2=1,4 45=63мм

18. 
    Толщина диска с связывающего ступицу и обод:
    

с=(1,0-1.1,2)  a=1,118=19,8 мм

19. 
    Внутренний диаметр обода D_k:
    

D_k=df-2a;

D_k2=307,77-2·18=260мм.

20. 
    Диаметр отверстий в диске D_o:
    

;

21. 
    Диаметр окружности центров отверстий D_oтв :
    

;


4.6 Силы в зацеплении конических колёс
Определение усилий в зацеплении зубчатых колес необходимо для расчета валов и подбора подшипников (рис.4.2).



Рисунок 4.2 – Силы в зацеплении конических передач
Окружная сила

(4.35)

где T₁=4610³ Н·мм; T₂=14110³ Н·мм;

d_m1=84 мм; d_m2=273 мм

Н;

Н.
Радиальная сила

(4.36)

где _w =20^о – угол зацепления.

Н;

Н.

Осевая сила

(4.37)

Н;

Н.