4. В среднем по 15% договоров страховая компания выплачивает страховую сумму. Найти вероятность того, что из десяти договоров с наступлением страхового случая будет связано с выплатой страховой суммы а три договора б менее двух договоров. 5

• Название: 4. В среднем по 15% договоров страховая компания выплачивает страховую сумму. Найти вероятность того, что из десяти договоров с наступлением страхового случая будет связано с выплатой страховой суммы а три договора б менее двух договоров. 5
• Дата: 19.04.2023
• Размер: 105.95 Kb.
• Имя файла: KR_teor_ver.docx
• Тип: Документы; #1075203

Вариант № 1

1. 
   Слово составлено из карточек, на каждой из которых написана одна буква. Карточки смешивают и вынимают без возврата по одной. Найти вероятность того, что карточки с буквами вынимаются в порядке следования букв заданного слова: а) «событие»; б) «статистика».
   

2. 
   Экспедиция издательства отправила газеты в три почтовых отделения. вероятность своевременной доставки газет в первое отделение равна 0,95, во второе отделение ‒ 0,9 и в третье ‒ 0,8. Найти вероятность следующих событий: а) только одно отделение получит газеты вовремя; б) хотя бы одно отделение получит газеты с опозданием.
   

3. В данный район изделия поставляются тремя фирмами в отношении 5:8:7. Среди продукции первой фирмы стандартные изделия составляют 90%, второй ‒ 85%, третьей ‒ 75%. Найти вероятность того, что: а) приобретенное изделие оказалось стандартным; б) нестандартным. Какова вероятность того, что оно изготовлено третьей фирмой?
4. В среднем по 15% договоров страховая компания выплачивает страховую сумму. Найти вероятность того, что из десяти договоров с наступлением страхового случая будет связано с выплатой страховой суммы: а) три договора; б) менее двух договоров.
5. Вероятность поражения вирусным заболеванием куста земляники равна 0,2. Составить закон распределения числа кустов земляники, зараженных вирусом, из четырех посаженных кустов. Вычислить математическое ожидание и дисперсию этой случайной величины.

Вариант № 2

1. 
   Пятитомное собрание сочинений расположено на полке в случайном порядке. Какова вероятность того, что книги стоят слева направо в порядке нумерации томов (от 1 до 5)?
   

2. 
   Прибор, работающий в течение времени t, состоит из трех узлов, каждый из которых независимо от других может за это время выйти из строя. Неисправность хотя бы одного узла выводит прибор из строя целиком. вероятность безотказной работы в течение времени tпервого узла равна 0,9, второго ‒ 0,95, третьего ‒ 0,8. Найти вероятность того, что в течение времени tприбор выйдет из строя.
   

3. Два стрелка сделали по одному выстрелу в мишень. Вероятность попадания в мишень для первого стрелка равна 0,6, а для второго ‒ 0,3. В мишени оказалась одна пробоина. Найти вероятность того, что она принадлежит первому стрелку.
4. Предполагается, что 10% открывающихся новых малых предприятий прекращают свою деятельность в течение года. Какова вероятность того, что из шести малых предприятий не более двух в течение года прекратят свою деятельность?
5. Стрелок ведет стрельбу по цели с вероятностью попадания при каждом выстреле 0,2. За каждое попадание он получает 5 очков, а в случае промаха очков ему не начисляют. Составить закон распределения числа очков, полученных стрелком за 3 выстрела, и вычислить математическое ожидание этой случайной величины.


Вариант № 3

1. 
   Среди 25 студентов, из которых 15 девушек, разыгрываются четыре билета, причем каждый может выиграть только один билет. Какова вероятность того, что среди обладателей билетов окажутся: а) четыре девушки; б) три юноши и одна девушка?
   

2. 
   Студент разыскивает нужную формулу в трех справочниках. Вероятность того, что формула содержится в первом, втором и третьем справочниках, равна соответственно 0,6, 0,7 и 0,8. Найти вероятность того, что эта формула содержится не менее чем в двух справочниках.
   

3. Вся продукция цеха проверяется двумя контролерами, причем первый контролер проверяет 55% изделий, а второй ‒ остальные. Вероятность того, что первый контролер пропустит нестандартное изделие, равна 0,01, второй ‒ 0,02. Взятое наудачу изделие, маркированное как стандартное, оказалось нестандартным. Найти вероятность того, что это изделие проверялось вторым контролером.
4. В банк отправлено 4000 пакетов денежных знаков. Вероятность того, что пакет содержит недостаточное или избыточное число денежных знаков, равна 0,0001. Найти вероятность того, что при проверке будет обнаружено: а) три ошибочно укомплектованных пакета; б) не более трех пакетов.
5. Из 10 телевизоров на выставке 4 оказались фирмы «Сони». Наудачу для осмотра выбрано 3. Составить закон распределения числа телевизоров фирмы «Сони» среди трех отобранных. Найти математическое ожидание и дисперсию этой случайной величины.


Вариант № 4

1. 
   Из 20 филиалов Сбербанка 10 расположены за чертой города. Для обследования случайным образом отобрано 5 филиалов. Какова вероятность того, что среди отобранных окажется в черте города: а) 3 филиала; б) хотя бы один?
   

2. 
   Произведено три выстрела по цели из орудия. Вероятность попадания при первом выстреле равна 0,75; при втором ‒ 0,8; при третьем ‒ 0,9. Определить вероятность того, что будет: а) три попадания; б) хотя бы одно попадание.
   

3. В одной урне 5 белых и 6 черных шаров, а в другой ‒ 4 белых и 8черных шаров. Из первой урны случайным образом вынимают 3 шара и опускают во вторую урну. После этого из второй также случайно вынимают 4 шара. Найти вероятность того, что все шары, вынутые из второй урны, белые.
4. Строительная фирма, занимающаяся установкой летних коттеджей, раскладывает рекламные листки по почтовым ящикам. Прежний опыт работы компании показывает, что примерно в одном случае из двух тысяч следует заказ. Найти вероятность того, что при размещении 100 тыс. листков число заказов будет: а) равно 48; б) находиться в границах от 45 до 55.
5. Случайная величина Х, сосредоточенная на интервале [2; 6], задана функцией распределения 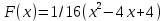. Найти вероятность того, что случайная величина Х примет значения: а) меньше 4; б) меньше 6; в) не меньше 3; г) не меньше 6.

Вариант № 5

1. 
   В магазине имеются 30 телевизоров, причем 20 из них импортных. Найти вероятность того, что среди 5 проданных в течение дня телевизоров окажется не менее 3 импортных телевизоров. Предполагается, что вероятности покупки телевизоров разных марок одинаковы.
   

2. 
   Мастер обслуживает четыре станка, работающих независимо друг от друга. Вероятность того, что первый станок в течение смены потребует внимания рабочего, равна 0,3, второй ‒ 0,6, третий ‒ 0,4 и четвертый ‒ 0,25. Найти вероятность того, что в течение смены хотя бы один станок не потребует внимания мастера.
   

3. В группе из 10 студентов, пришедших на экзамен, 3 ‒ подготовлены отлично, 4‒ хорошо, 2 ‒ посредственно и 1 ‒ плохо. В экзаменационных билетах имеется 20 вопросов. Отлично подготовленный студент может ответить на все 20 вопросов, хорошо подготовленный ‒ на 16, посредственно ‒ на 10, плохо ‒ на 5. Вызванный наугад студент ответил на три произвольно заданных вопроса. Найти вероятность того, что студент подготовлен: а) отлично; б) плохо.
4. Аудиторную работу по теории вероятностей с первого раза успешно выполняют 50% студентов. Найти вероятность того, что из 400 студентов работу успешно выполнят: а) 180 студентов; б) не менее 180 студентов.
5. Случайная величина Х задана функцией распределения



Найти: а) плотность вероятности 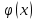; б) математическое ожидание М(Х); в) дисперсию D(X).
Вариант № 6

1. В первом ящике 2 красных и 5 синих папок, во втором – 4 красных и 3 синих. Из первого ящика переложили 2 папки во второй, после чего из второго ящика наудачу достали одну папку. Какова вероятность того, что она красного цвета?

2. Вероятность сдачи студентом контрольной работы в срок равна 0,7. Найти вероятность того, что из 5 студентов вовремя сдадут контрольную работу:

а) ровно 3 студента; б) хотя бы один студент.

3. Всхожесть хранящегося на складе зерна равна 80%. Отбираются 400 зерен. Определить вероятность того, что из отобранных зерен взойдут:

а) ровно 303; б) от 250 до 330.

4. Котировки акций могут быть размещены в Интернете на трех сайтах. Материал есть на первом сайте с вероятностью 0,7, на втором – с вероятностью 0,6, на третьем – с вероятностью 0,8. Студент переходит к новому сайту только в том случае, если не найдет данных на предыдущем. Составить закон распределения числа сайтов, которые посетит студент.

Найти:

а) функцию распределения этой случайной величины и построить ее график;

б) математическое ожидание и дисперсию этой случайной величины.

Вариант № 7
1. Дано восемь карточек с буквами Н, М, И, И, Я, Л, Л, О. Найти вероятность того, что:

а) получится слово «ЛОМ», если наугад одна за другой выбираются три карточки и располагаются в ряд в порядке появления;

б) получится слово «МОЛНИЯ», если наугад одна за другой выбираются шесть карточек.

2. По телевидению с 1 сентября начинают показывать 4 новых сериала. Вероятность того, что сериал продлится до Нового года, равна 0,3. Найти вероятность того, что до Нового года из этих сериалов продлится:

а) ровно 2; б) хотя бы один.

3. В филиале института 1000 студентов. После окончания занятий в среднем каждый десятый студент занимается в читальном зале. Сколько посадочных мест нужно иметь, чтобы с вероятностью 0,9545 их хватало всем студентам филиала.

	0	1	2
	0,1	?	0,7

4. Законы распределения независимых случайных величин X и Y приведены в таблицах: X: Y:

	1	3
	0,6	?

Найти:

а) вероятности   и 

б) закон распределения случайной величины 

в) математическое ожидание   и дисперсию D(Z);
Вариант № 8

3. 
   Слово составлено из карточек, на каждой из которых написана одна буква. Карточки смешивают и вынимают без возврата по одной. Найти вероятность того, что карточки с буквами вынимаются в порядке следования букв заданного слова: а) «событие»; б) «статистика».
   

4. 
   Экспедиция издательства отправила газеты в три почтовых отделения. вероятность своевременной доставки газет в первое отделение равна 0,95, во второе отделение ‒ 0,9 и в третье ‒ 0,8. Найти вероятность следующих событий: а) только одно отделение получит газеты вовремя; б) хотя бы одно отделение получит газеты с опозданием.
   

3. В данный район изделия поставляются тремя фирмами в отношении 5:8:7. Среди продукции первой фирмы стандартные изделия составляют 90%, второй ‒ 85%, третьей ‒ 75%. Найти вероятность того, что: а) приобретенное изделие оказалось стандартным; б) нестандартным. Какова вероятность того, что оно изготовлено третьей фирмой?
4. В среднем по 15% договоров страховая компания выплачивает страховую сумму. Найти вероятность того, что из десяти договоров с наступлением страхового случая будет связано с выплатой страховой суммы: а) три договора; б) менее двух договоров.
5. Вероятность поражения вирусным заболеванием куста земляники равна 0,2. Составить закон распределения числа кустов земляники, зараженных вирусом, из четырех посаженных кустов. Вычислить математическое ожидание и дисперсию этой случайной величины.

Вариант № 9

3. 
   Пятитомное собрание сочинений расположено на полке в случайном порядке. Какова вероятность того, что книги стоят слева направо в порядке нумерации томов (от 1 до 5)?
   

4. 
   Прибор, работающий в течение времени t, состоит из трех узлов, каждый из которых независимо от других может за это время выйти из строя. Неисправность хотя бы одного узла выводит прибор из строя целиком. вероятность безотказной работы в течение времени tпервого узла равна 0,9, второго ‒ 0,95, третьего ‒ 0,8. Найти вероятность того, что в течение времени tприбор выйдет из строя.
   

3. Два стрелка сделали по одному выстрелу в мишень. Вероятность попадания в мишень для первого стрелка равна 0,6, а для второго ‒ 0,3. В мишени оказалась одна пробоина. Найти вероятность того, что она принадлежит первому стрелку.
4. Предполагается, что 10% открывающихся новых малых предприятий прекращают свою деятельность в течение года. Какова вероятность того, что из шести малых предприятий не более двух в течение года прекратят свою деятельность?
5. Стрелок ведет стрельбу по цели с вероятностью попадания при каждом выстреле 0,2. За каждое попадание он получает 5 очков, а в случае промаха очков ему не начисляют. Составить закон распределения числа очков, полученных стрелком за 3 выстрела, и вычислить математическое ожидание этой случайной величины.


Вариант № 10

3. 
   Среди 25 студентов, из которых 15 девушек, разыгрываются четыре билета, причем каждый может выиграть только один билет. Какова вероятность того, что среди обладателей билетов окажутся: а) четыре девушки; б) три юноши и одна девушка?
   

4. 
   Студент разыскивает нужную формулу в трех справочниках. Вероятность того, что формула содержится в первом, втором и третьем справочниках, равна соответственно 0,6, 0,7 и 0,8. Найти вероятность того, что эта формула содержится не менее чем в двух справочниках.
   

3. Вся продукция цеха проверяется двумя контролерами, причем первый контролер проверяет 55% изделий, а второй ‒ остальные. Вероятность того, что первый контролер пропустит нестандартное изделие, равна 0,01, второй ‒ 0,02. Взятое наудачу изделие, маркированное как стандартное, оказалось нестандартным. Найти вероятность того, что это изделие проверялось вторым контролером.
4. В банк отправлено 4000 пакетов денежных знаков. Вероятность того, что пакет содержит недостаточное или избыточное число денежных знаков, равна 0,0001. Найти вероятность того, что при проверке будет обнаружено: а) три ошибочно укомплектованных пакета; б) не более трех пакетов.
5. Из 10 телевизоров на выставке 4 оказались фирмы «Сони». Наудачу для осмотра выбрано 3. Составить закон распределения числа телевизоров фирмы «Сони» среди трех отобранных. Найти математическое ожидание и дисперсию этой случайной величины.

Вариант № 11

3. 
   Из 20 филиалов Сбербанка 10 расположены за чертой города. Для обследования случайным образом отобрано 5 филиалов. Какова вероятность того, что среди отобранных окажется в черте города: а) 3 филиала; б) хотя бы один?
   

4. 
   Произведено три выстрела по цели из орудия. Вероятность попадания при первом выстреле равна 0,75; при втором ‒ 0,8; при третьем ‒ 0,9. Определить вероятность того, что будет: а) три попадания; б) хотя бы одно попадание.
   

3. В одной урне 5 белых и 6 черных шаров, а в другой ‒ 4 белых и 8черных шаров. Из первой урны случайным образом вынимают 3 шара и опускают во вторую урну. После этого из второй также случайно вынимают 4 шара. Найти вероятность того, что все шары, вынутые из второй урны, белые.
4. Строительная фирма, занимающаяся установкой летних коттеджей, раскладывает рекламные листки по почтовым ящикам. Прежний опыт работы компании показывает, что примерно в одном случае из двух тысяч следует заказ. Найти вероятность того, что при размещении 100 тыс. листков число заказов будет: а) равно 48; б) находиться в границах от 45 до 55.
5. Случайная величина Х, сосредоточенная на интервале [2; 6], задана функцией распределения 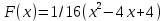. Найти вероятность того, что случайная величина Х примет значения: а) меньше 4; б) меньше 6; в) не меньше 3; г) не меньше 6.

Вариант № 12

3. 
   В магазине имеются 30 телевизоров, причем 20 из них импортных. Найти вероятность того, что среди 5 проданных в течение дня телевизоров окажется не менее 3 импортных телевизоров. Предполагается, что вероятности покупки телевизоров разных марок одинаковы.
   

4. 
   Мастер обслуживает четыре станка, работающих независимо друг от друга. Вероятность того, что первый станок в течение смены потребует внимания рабочего, равна 0,3, второй ‒ 0,6, третий ‒ 0,4 и четвертый ‒ 0,25. Найти вероятность того, что в течение смены хотя бы один станок не потребует внимания мастера.
   

3. В группе из 10 студентов, пришедших на экзамен, 3 ‒ подготовлены отлично, 4‒ хорошо, 2 ‒ посредственно и 1 ‒ плохо. В экзаменационных билетах имеется 20 вопросов. Отлично подготовленный студент может ответить на все 20 вопросов, хорошо подготовленный ‒ на 16, посредственно ‒ на 10, плохо ‒ на 5. Вызванный наугад студент ответил на три произвольно заданных вопроса. Найти вероятность того, что студент подготовлен: а) отлично; б) плохо.
4. Аудиторную работу по теории вероятностей с первого раза успешно выполняют 50% студентов. Найти вероятность того, что из 400 студентов работу успешно выполнят: а) 180 студентов; б) не менее 180 студентов.
5. Случайная величина Х задана функцией распределения



Найти: а) плотность вероятности 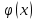; б) математическое ожидание М(Х); в) дисперсию D(X).
Вариант № 13

1. В первом ящике 2 красных и 5 синих папок, во втором – 4 красных и 3 синих. Из первого ящика переложили 2 папки во второй, после чего из второго ящика наудачу достали одну папку. Какова вероятность того, что она красного цвета?

2. Вероятность сдачи студентом контрольной работы в срок равна 0,7. Найти вероятность того, что из 5 студентов вовремя сдадут контрольную работу:

а) ровно 3 студента; б) хотя бы один студент.

3. Всхожесть хранящегося на складе зерна равна 80%. Отбираются 400 зерен. Определить вероятность того, что из отобранных зерен взойдут:

а) ровно 303; б) от 250 до 330.

4. Котировки акций могут быть размещены в Интернете на трех сайтах. Материал есть на первом сайте с вероятностью 0,7, на втором – с вероятностью 0,6, на третьем – с вероятностью 0,8. Студент переходит к новому сайту только в том случае, если не найдет данных на предыдущем. Составить закон распределения числа сайтов, которые посетит студент.

Найти:

а) функцию распределения этой случайной величины и построить ее график;

б) математическое ожидание и дисперсию этой случайной величины.

Вариант № 14
1. Дано восемь карточек с буквами Н, М, И, И, Я, Л, Л, О. Найти вероятность того, что:

а) получится слово «ЛОМ», если наугад одна за другой выбираются три карточки и располагаются в ряд в порядке появления;

б) получится слово «МОЛНИЯ», если наугад одна за другой выбираются шесть карточек.

2. По телевидению с 1 сентября начинают показывать 4 новых сериала. Вероятность того, что сериал продлится до Нового года, равна 0,3. Найти вероятность того, что до Нового года из этих сериалов продлится:

а) ровно 2; б) хотя бы один.

3. В филиале института 1000 студентов. После окончания занятий в среднем каждый десятый студент занимается в читальном зале. Сколько посадочных мест нужно иметь, чтобы с вероятностью 0,9545 их хватало всем студентам филиала.

	0	1	2
	0,1	?	0,7

4. Законы распределения независимых случайных величин X и Y приведены в таблицах: X: Y:

	1	3
	0,6	?

Найти:

а) вероятности   и 

б) закон распределения случайной величины 

в) математическое ожидание   и дисперсию D(Z);