44. Лемма 2 для доказательства теоремы о конечности дерева достижимости сети Петри. Лемма 2
 Скачать 1.09 Mb.
|
 44. Лемма 2 для доказательства теоремы о конечности дерева достижимости сети Петри.Лемма 2. Всякая бесконечная последовательность из расширенного множества натуральных чисел содержит бесконечную неубывающую подпоследовательность. 45. Лемма 3 для доказательства теоремы о конечности дерева достижимости сети Петри. Лемма 3. Всякая бесконечная последовательность n-мерных векторов над расширенным множеством натуральных чисел содержит бесконечную неубывающую подпоследовательность. 46. Терема о конечности дерева достижимости сети Петри. Терема о конечности усеченного дерева достижимости сети Петри. Усеченное дерево достижимости сети Петри конечно. 47. Решение задачи безопасности и ограниченности сетей Петри на основе дерева достижимости. Сеть Петри ограничена тогда и только тогда, когда символ  отсутствует в ее дереве достижимости.В этом случае покомпонентное исследование вершин усеченного ДД позволяет установить безопасность или ограниченность для каждой отдельной позиции, после чего сделать вывод о сети в целом. Наибольшее значение компоненты маркировки, соответствующей некоторой позиции есть граница числа фишек этой позиции. Если граница для всех позиций не превышает 1, сеть безопасна. 48. Решение задачи сохранения сетей Петри на основе дерева достижимости. 49. Решение задачи покрываемости и достижимости сетей Петри на основе дерева достижимости. Проблемы, возникающие в случае наличия неограниченной позиции. Пример. Решение затруднено в случае, когда ДД содержит символ 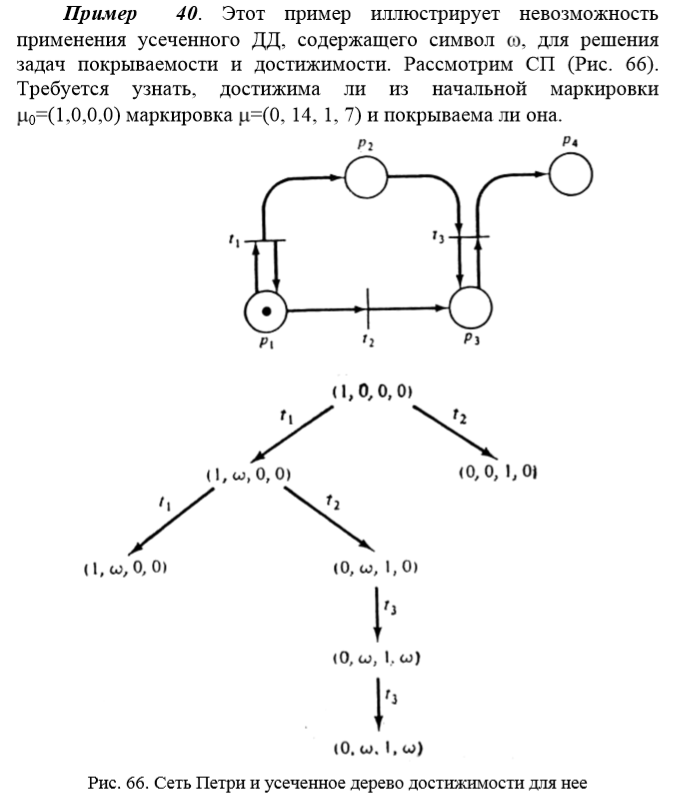. Если дерево не содержит символ , то эти задачи успешно решаются. Рассмотрим алгоритм решения этих задач для дерева, не содержащего символ .     50. Анализ свойств сетей на основе использования матричного подхода: матрицы D-, D+, пример построения матриц для сети Петри.    51. Составная матрица изменений (матрица инцидентности). Пример. Замечания по применению матричного подхода.   52. Получение фундаментального уравнения сети Петри.  53. Роль фундаментального уравнения. Утверждения 1, 2.  |