5 вариант Егор А2 Б9
 Скачать 1.54 Mb. Скачать 1.54 Mb.
|
|
5 вариант Егор А=2 Б=9 Задача 5.1. За отчетный период деятельность группы предприятий характеризуется следующими данными на основании статистического и финансового учета:
По данным таблицы произвести группировку предприятий по размеру основных фондов, выделив 4 группы (60%). Установить зависимость прибыли предприятия от численности работников, стоимости основных фондов и объема выпускаемой продукции (30%). Сделать выводы (10%). Решение: i= (Хmax— Xmin)/4 i=(1599-178)/4=355,25
i= (Хmax— Xmin)/4 i=(111-25)/4=21,5
Вывод: Как видно из приведенных выше таблиц, предприятия по размеру прибыли распределены неравномерно. Наибольший объем валовой продукции 5344 млн.руб, наибольшая численность персонала 1976,а наибольшая среднегодовая стоимость основынх производственных фондов—4494 млн принадлежит предприятиям с прибылью от 68 тыс.руб до 89,5 тыс руб. Задача 5.2. Имеются данные о дальности перевозок и грузообороте 5 грузовых автомашин за день. Определить среднюю дальность перевозки 1 тонны груза (80%)
Обоснуйте правильность выбора формулы для расчета (20%). Решение: Формула средней гармонической взвешенной: 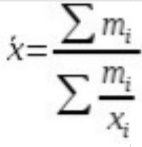 Х=(61+48+51+138+56)/(61/9+48/14+51/12+138/17+56/11)=12.7 Вывод: потому что средняя гармоническая взвешенная применяется тогда, когда известны варианты (х) и объемы признаков (M - xf), но частоты отдельным вариантам х не известны, а входят сомножителями в произведение, как в данном случае когда частотой будет являться кол-во товара для перевозки Задача 5.3. В целях контроля за соблюдением норм расхода сырья проведено выборочное обследование партии готовой продукции. При механическом способе отбора 2 % изделий получены следующие данные о весе обследованных единиц:
При условии, что к стандартной продукции относятся изделия с весом от 2001 до 2100 г, установите для всей партии: 1) с вероятностью 0,95 возможны пределы удельного веса стандартной продукции (50%); 2) с вероятность 0,997 возможные пределы среднего веса одного изделия в генеральной совокупности (50%) Решение: 1) n=8+29+62+19+6=124 N=2%*n=2*124=248 m=29+62=91 w=m/n=91/124=0.73 t=2 (по таблице Лапласса) 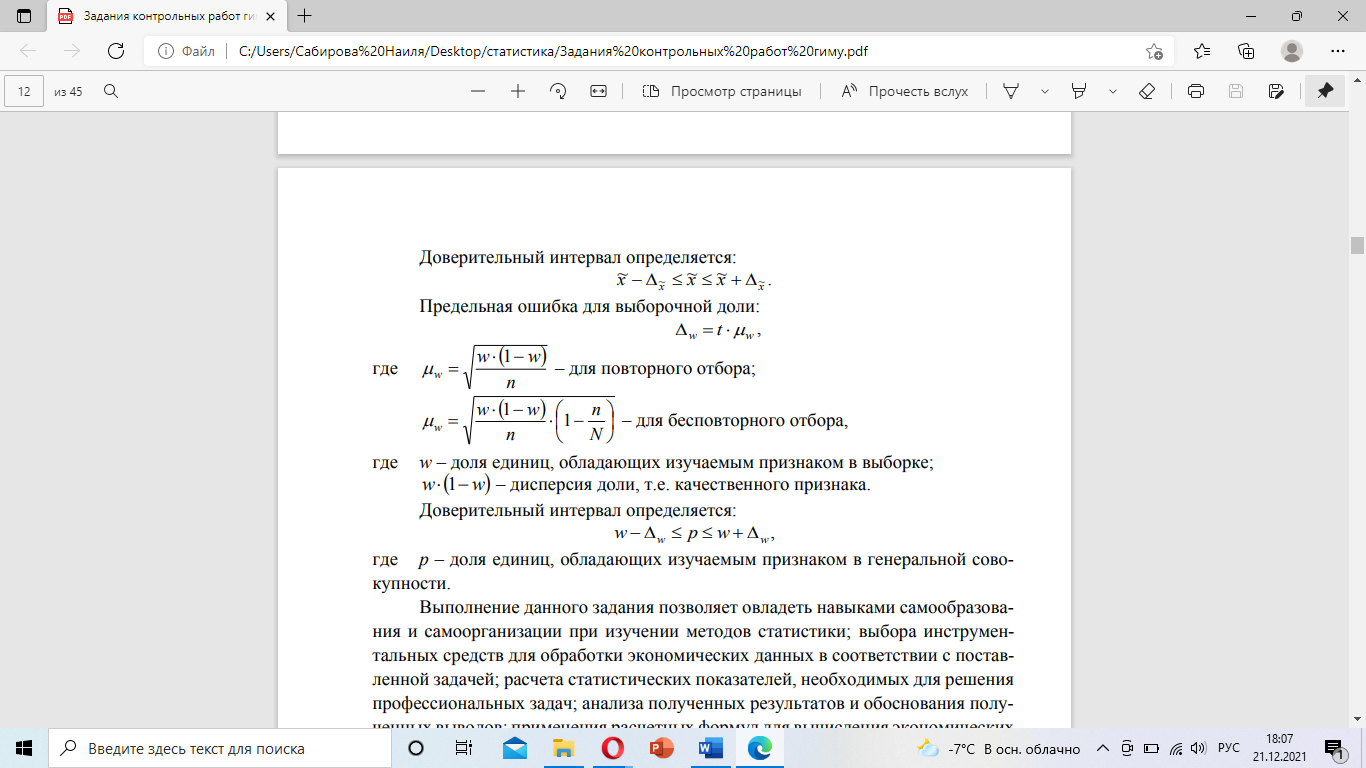 Фото 1 Предельная ошибка для выборочной доли:  w=2*0,03=0,06 0,73-0,06≤p≤0,73+0,06 0,67≤p≤0,79 2) Хв=∑xf/∑f=(1975,5*8+2025,5*29+2075,5*62+2125,5*19+2174,5*6)/( 8+29+62+19+6)= 256656/124=2069,8 формула σ2=(1975,5-2069,8)2*8+(2025,5-2069,8)2*29+(2075,5-2069,8)2*62+(2125,5-2069,8)2*19+(2174,5-2069,8)2*6)/( 124)=2056,7  Фото 2 x=3*2,87=8,61 2069,8-8,61≤x≤2069,8+8,61 2061,19≤x≤2078,41 Задача 5.4. Имеются следующие данные о распределении строительных бригад области по производительности труда и себестоимости единицы продукции:
Рассчитайте коэффициент взаимной сопряженности Пирсона (80%). Сделайте вывод (20%). Решение: Коэффициент сопряженности Пирсона- 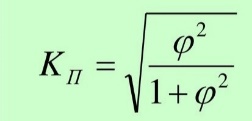  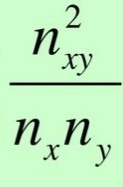 1=(112/78+222/70+302/68)/63= 0,34445813 1=(112/78+222/70+302/68)/63= 0,34445813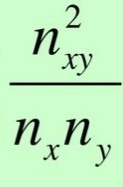 2=(302/78+292/70+312/68)/90=0,41872334 2=(302/78+292/70+312/68)/90=0,41872334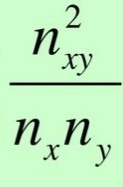 3=(372/78+222/70+302/68)/63=0,3718891 3=(372/78+222/70+302/68)/63=0,3718891 =(0,34445813+0,41872334+0,3718891)-1=0,135071 =(0,34445813+0,41872334+0,3718891)-1=0,135071Фото3 Вывод: коэффициент взаимной сопряженности Пирсона заметно отличается от нуля - между себестоимостью продукции и производительностью труда существует слабая связь. Задача 5.5. Имеются следующие данные о товарных запасах торгового предприятия (тыс. руб., сопоставимые данные):
Определите абсолютное (40%) и относительное (40%) изменение средней суммы товарных запасов в 2017 г. по сравнению с 2014, 2015 и 2016 гг. Интерпретируйте полученные результаты (20%). Решение:
  П=(5+4-56,25)/3=-15,75  Задача 5.6. Имеются данные о себестоимости и объеме продукции предприятия. Определите: 1) агрегатный индекс себестоимости продукции (по модели Пааше) (30%); 2) агрегатный индекс физического объема продукции (по модели Ласпейреса) (30%); 3) общий индекс затрат на производство (30%).
Покажите взаимосвязь между индексами (10%). Решение: индекс себестоимости (по модели Пааше): 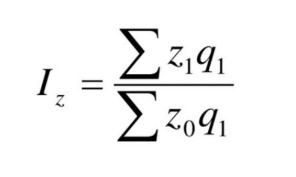 I=(148*1800+99*4700+112*5400)/(138*1800+99*4700+112*5400)= 1,010769814 индекс физического объема(Ласпейреса):  I=(1800*138+4700*99+5400*112)/(1900*138+4100*99+5900*112)= 0,992173978 индекс затрат на производство 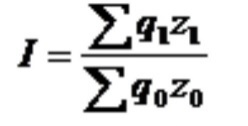 I= (1800*148+4700*89+5400*120)/(1900*138+4100*99+5900*112)= 1,002859508 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
