Глава II. Задания из ЕГЭ по планиметрии
2.1. Примеры решения задач по теме: «Треугольники и их виды»
Рассмотрим одну из задач, в которой ключевым моментом решения являлось подобие треугольников и составление соответствующей пропорции. В данной задаче представлено непривычное расположение подобных треугольников, что затрудняет и их распознавание и запись пропорциональности сторон.
Задача 1. Точка Н лежит на стороне АО треугольника АОМ. Известно, что АН=4, ОН = 12,  МAО= 30 МAО= 30 , ,  АМН = АМН =  АОМ. Найдите площадь треугольника АНМ. АОМ. Найдите площадь треугольника АНМ.
РЕШЕНИЕ.
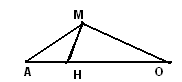
|
1)  АМН подобен АМН подобен  АОМ по двум углам: АОМ по двум углам:
 А – общий, А – общий,  АМН = АМН =  АОМ по условию. Из подобия следует АОМ по условию. Из подобия следует 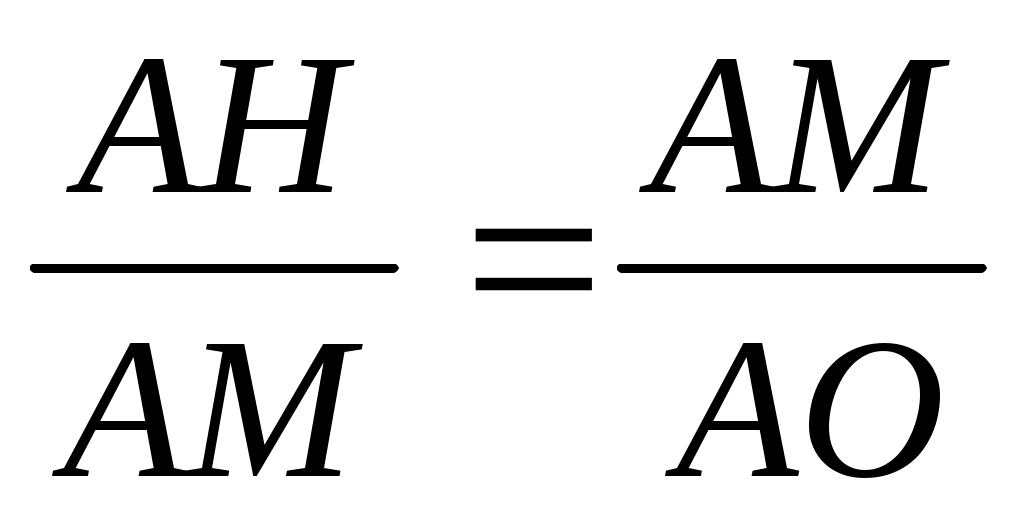 , , 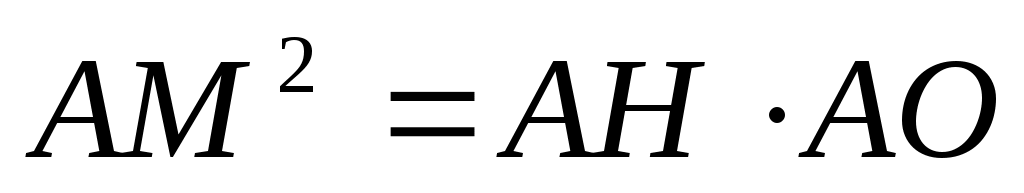 , , 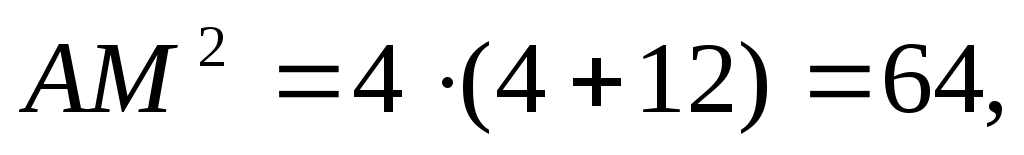 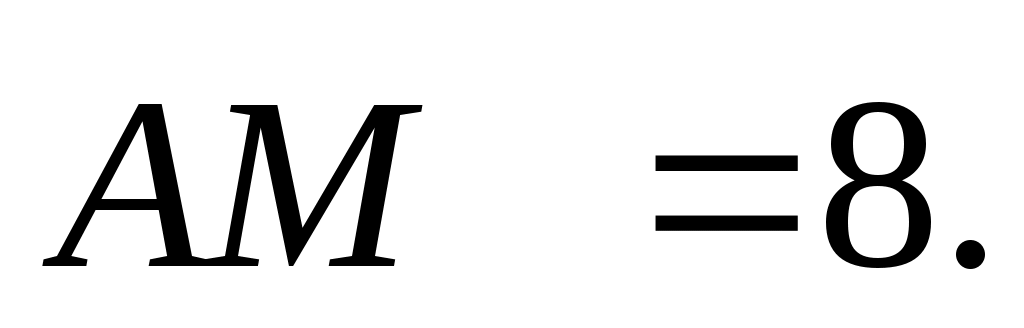
|
2) 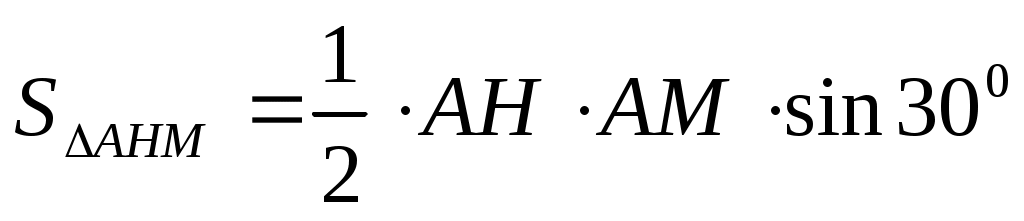 , , 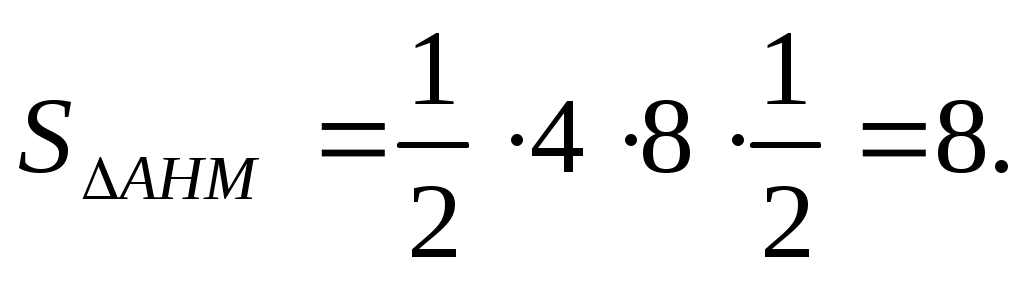
Ответ: 8.
|
Применение теоремы косинусов в решении ряда задач было осложнено тем, что эта теорема использовалась не для прямых вычислений, а для составления уравнения.
Рассмотрим задачу на составление уравнения с помощью теоремы косинусов и на применение свойства медианы (медиана делит треугольник на два равновеликих треугольника)
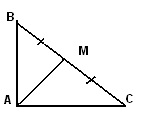
Задача 2. В  АВС проведена медиана АМ, причем АВС проведена медиана АМ, причем  МАС = 45 МАС = 45 .Найдите площадь треугольника АВС, если АС = .Найдите площадь треугольника АВС, если АС = , ВС = 10. , ВС = 10.
РЕШЕНИЕ.

|
1)Медиана АМ делит ВС пополам, поэтому ВМ = МС=5. Запишем для МАС теорему косинусов: МАС теорему косинусов: 

Решив уравнение 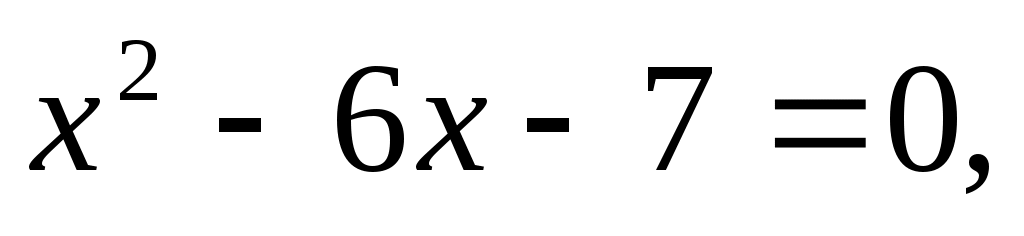 получим получим 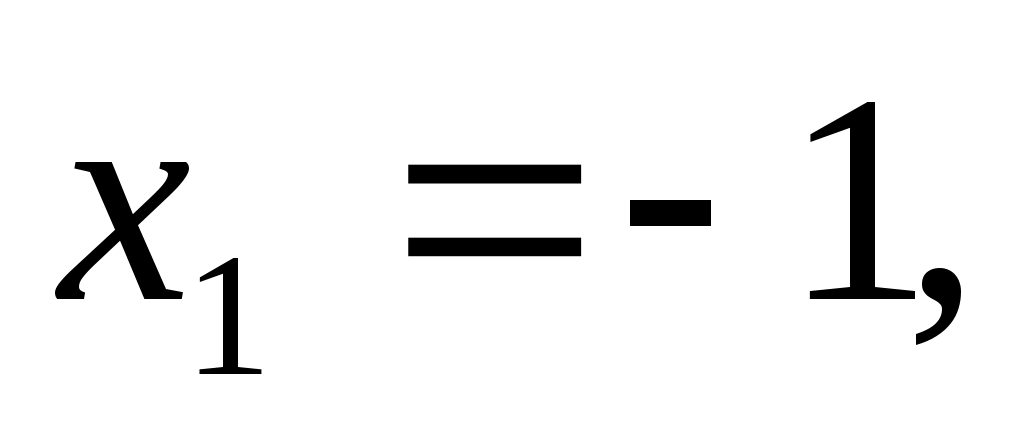 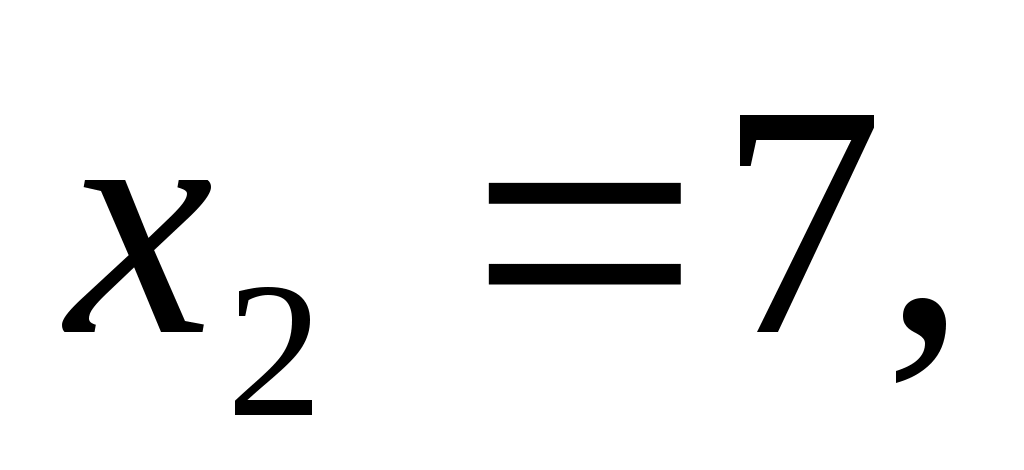 откуда АМ = 7. откуда АМ = 7.
|
2) 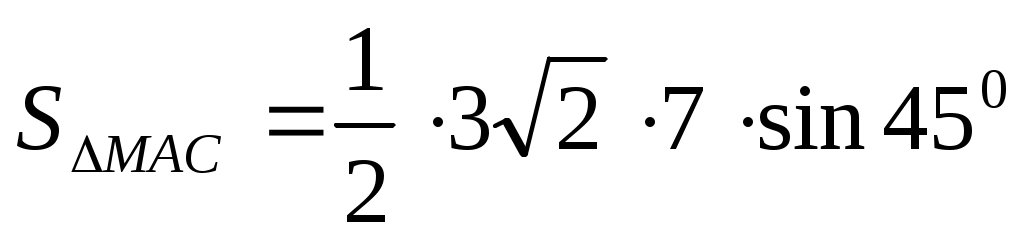 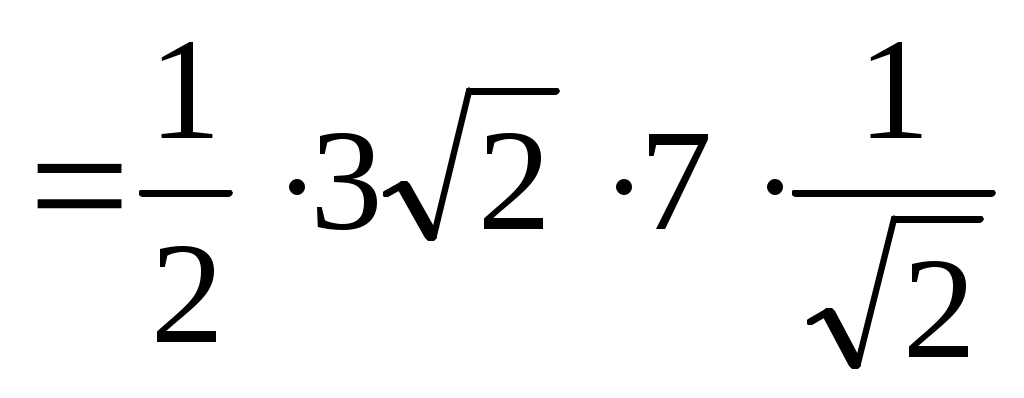 = 10,5. = 10,5.
3) Так как медиана делит треугольник на два равновеликих треугольника, то

Ответ: 21.
|
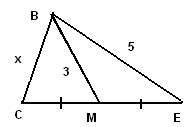
Задача 3.В треугольнике ВСЕ медиана ВМ равна 3, СЕ =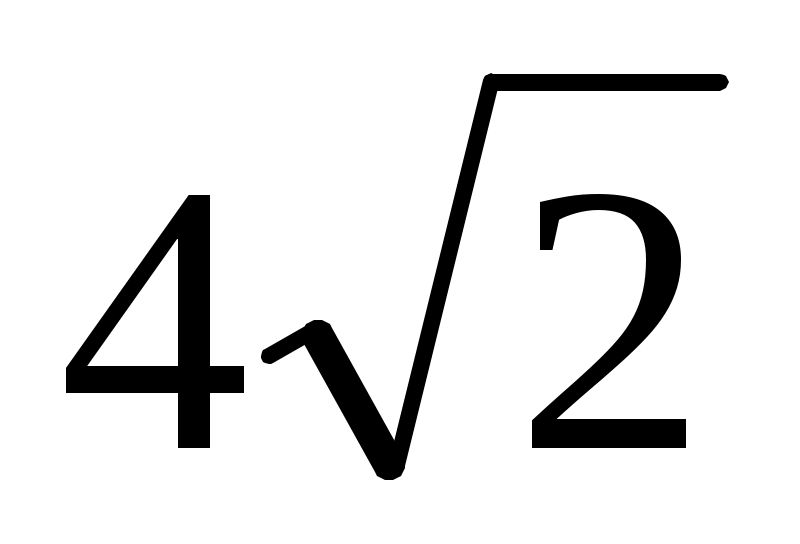 , ВЕ = 5. Найдите сторону ВС. , ВЕ = 5. Найдите сторону ВС.
РЕШЕНИЕ.
|
1)Из ΔВМЕ найдем cosE по теореме косинусов:
 , ,
 

|
2) Из  ВСЕ по теореме косинусов: ВСЕ по теореме косинусов: 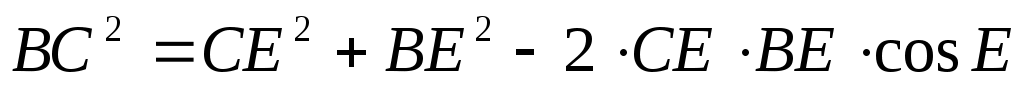 , , 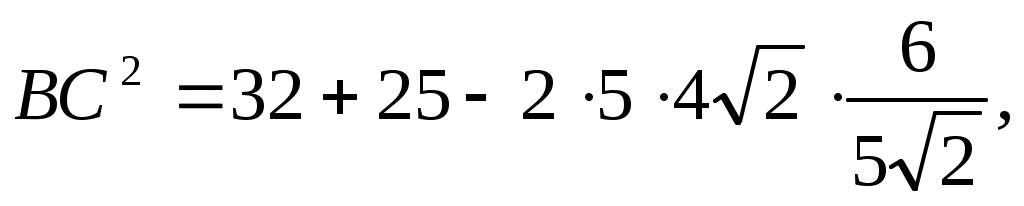 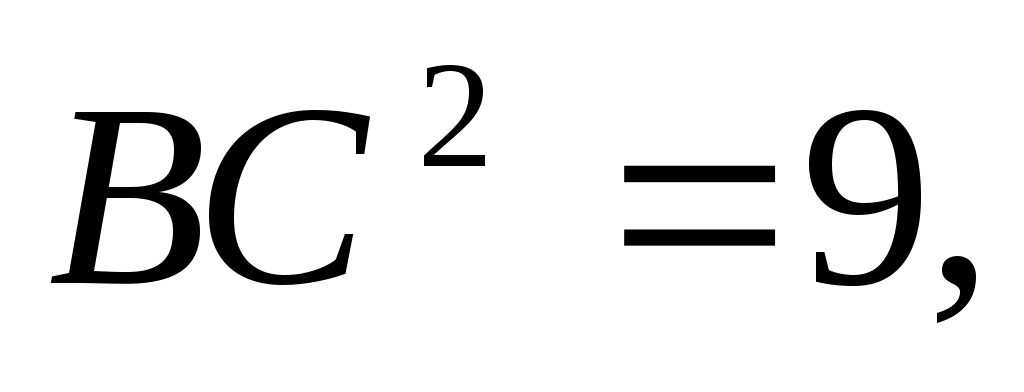 ВС = 3. ВС = 3.
Ответ: 3.
|
Задача 4.Один из катетов прямоугольного треугольника равен 15, а проекция второго катета на гипотенузу равна 16. Найдите диаметр окружности, описанной около этого треугольника.
РЕШЕНИЕ.
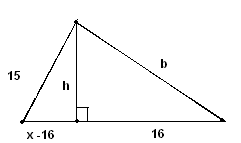
Ответ: 25.
|
1)Пусть гипотенуза равна х, тогда
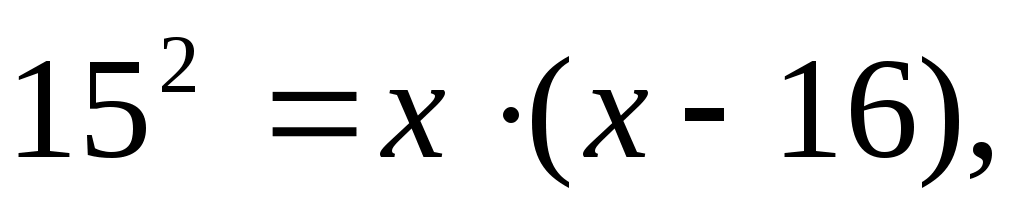 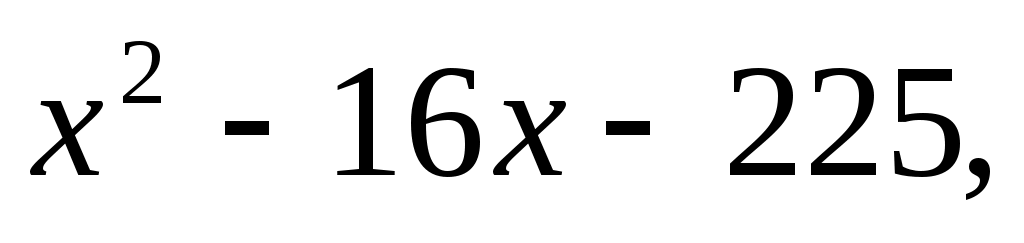
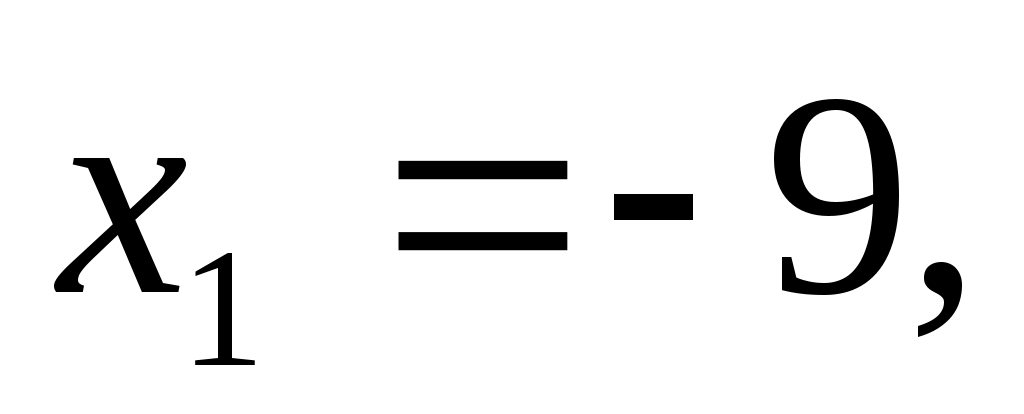 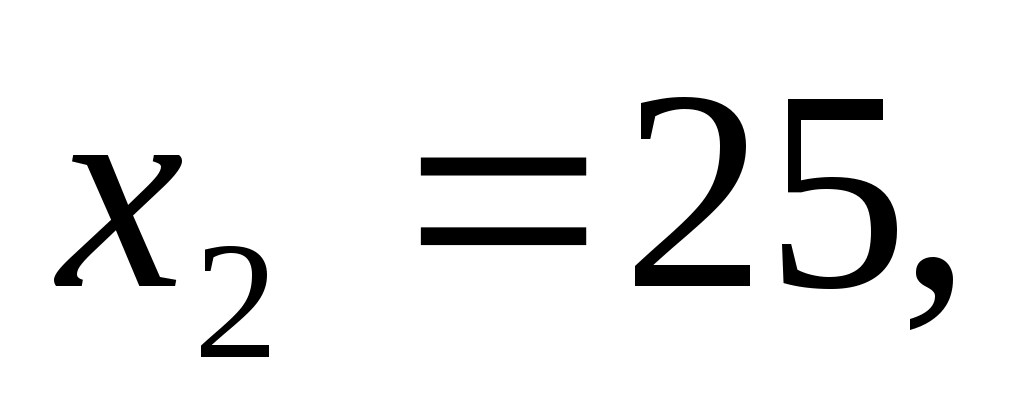 гипотенуза равна 25. гипотенуза равна 25.
Диаметр окружности, описанной около этого прямоугольного треугольника равен гипотенузе.
|
P.S. Вообще говоря, здесь легко найти и остальные элементы данного треугольника: 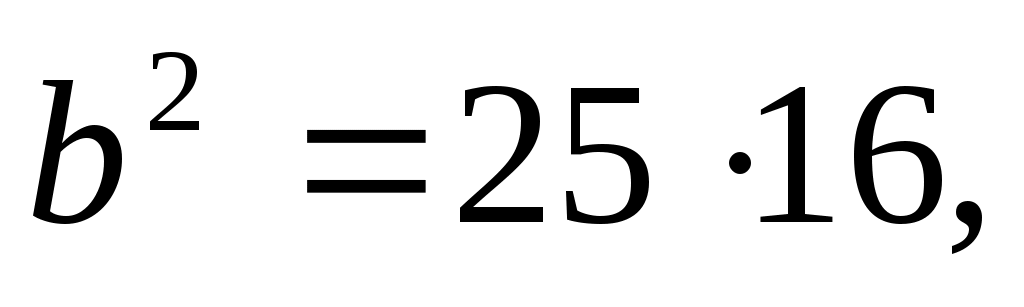 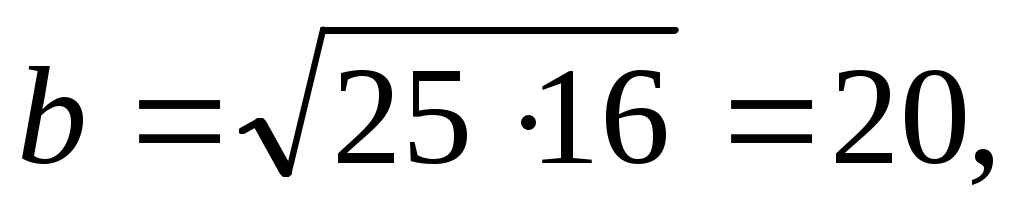 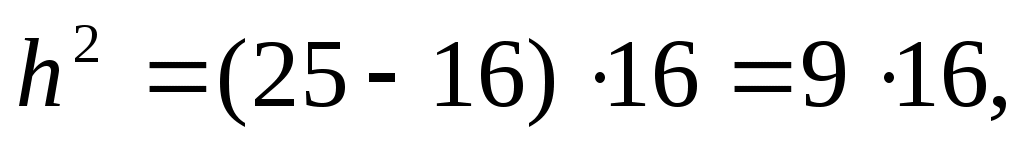 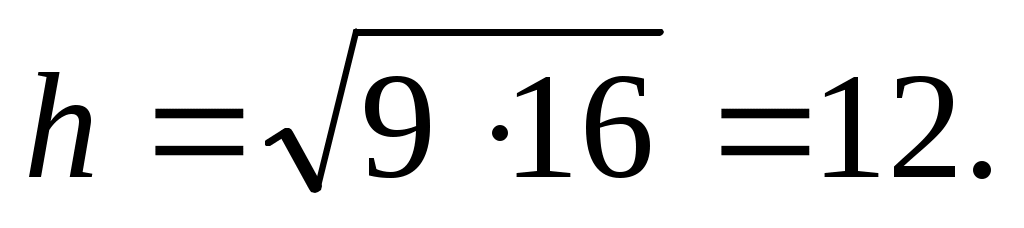
Эти элементы можно было бы вычислять, используя подобие треугольников или определение синуса (или косинуса) угла для составления пропорции, а затем применив теорему Пифагора.
Например, для вычисления гипотенузы можно составить пропорцию 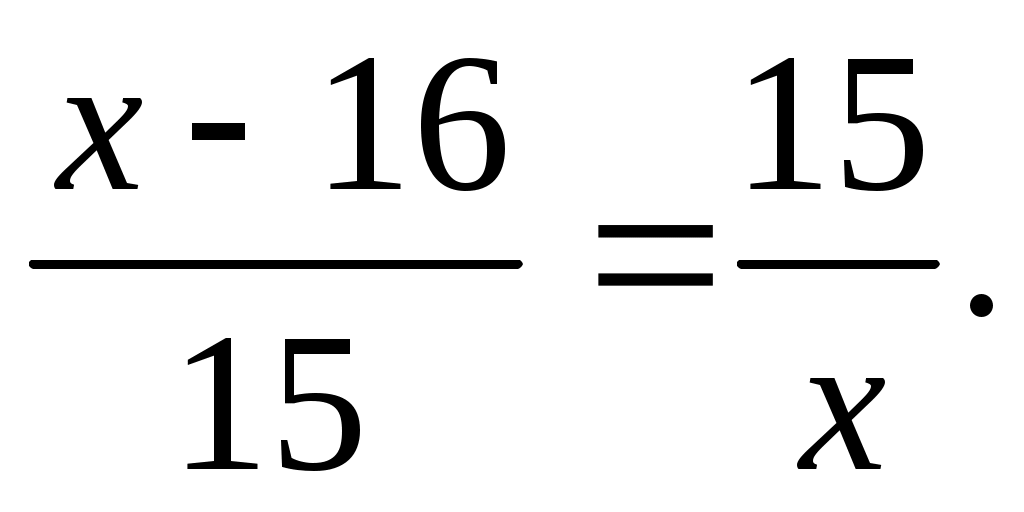 Однако этот путь решения тоже зачастую вызывает трудности у учащихся. Однако этот путь решения тоже зачастую вызывает трудности у учащихся.
Задача 5. Высоты АН и ВК равнобедренного треугольника АВС с основанием ВС пересекаются в точке О так, что ВО = 5, ОК = 3. Найдите АН.
РЕШЕНИЕ.
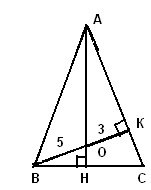
|
1) Высота АН, проведенная к основанию равнобедренного  АВС одновременно является и биссектрисой АВС одновременно является и биссектрисой АВК, тогда по свойству биссектрисы треугольника, она делит противоположную сторону ВК на отрезки, пропорциональные прилежащим сторонам, т.е. АВК, тогда по свойству биссектрисы треугольника, она делит противоположную сторону ВК на отрезки, пропорциональные прилежащим сторонам, т.е. 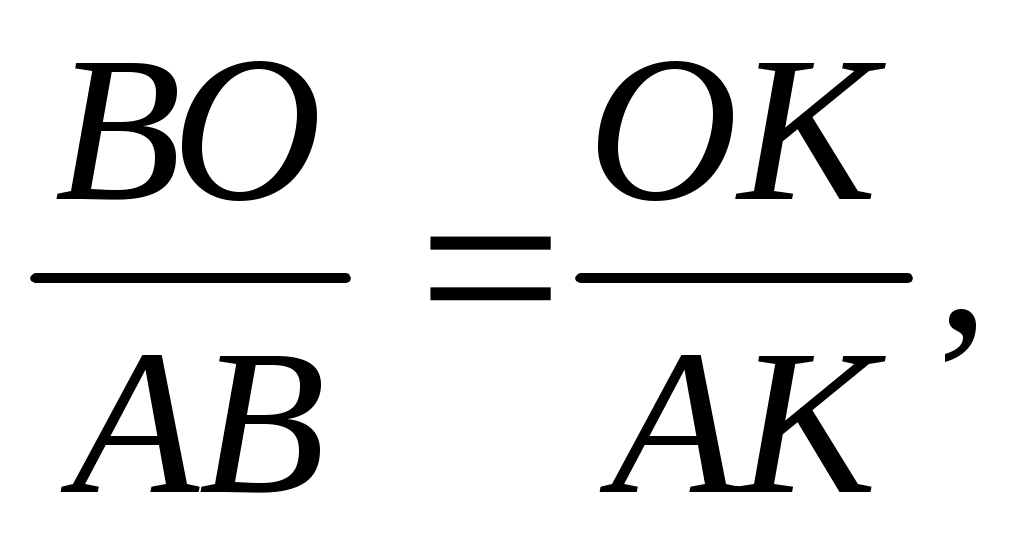 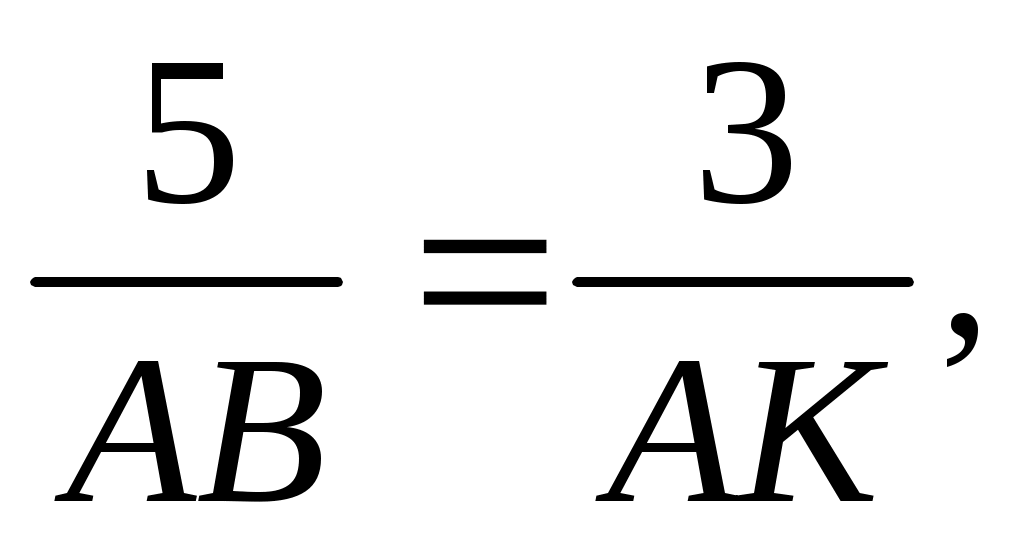 отсюда отсюда 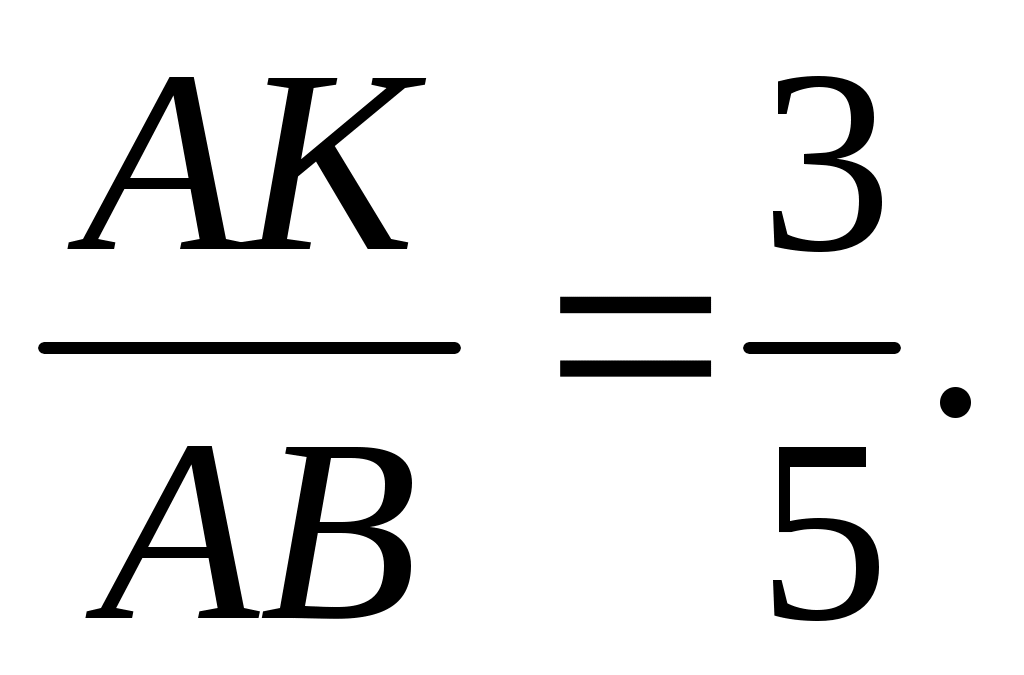
2)Пусть АК = 3х, АВ = 5х. Из прямоугольного  АВК по теореме Пифагора получаем АВК по теореме Пифагора получаем
|
уравнение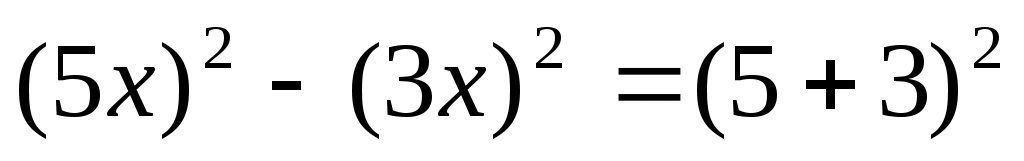 . .
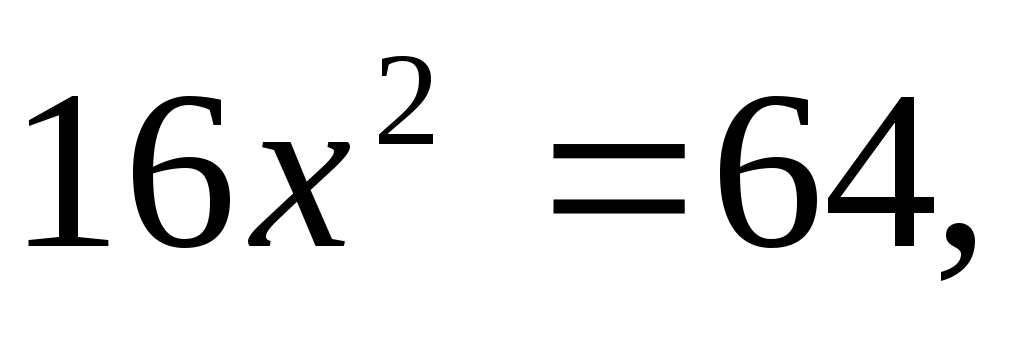 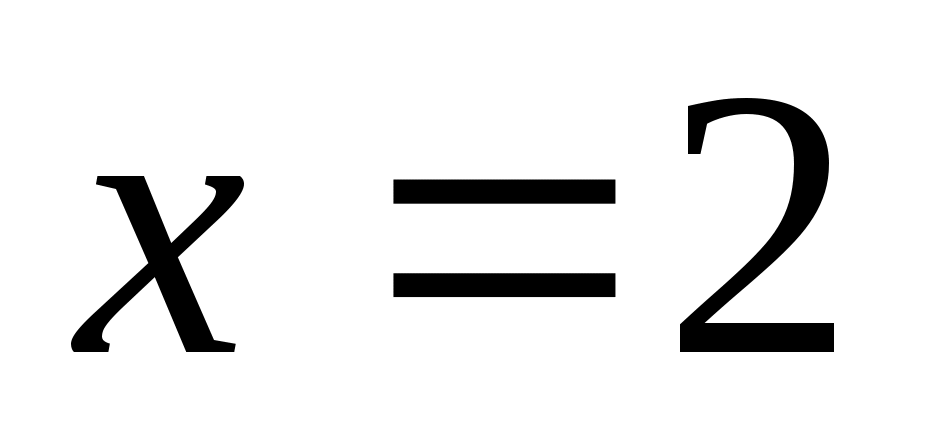 . АВ = АС = 5·2 = 10, АК=3 · 2 = 6, КС = 10 – 6 = 4. . АВ = АС = 5·2 = 10, АК=3 · 2 = 6, КС = 10 – 6 = 4.
3) Из прямоугольного  ВКС по теореме Пифагора: ВКС по теореме Пифагора: 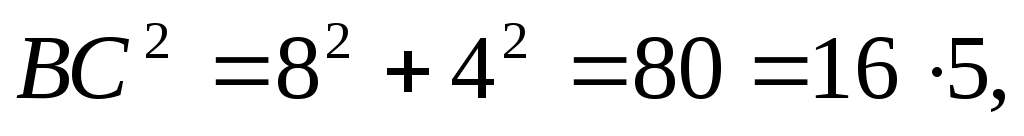 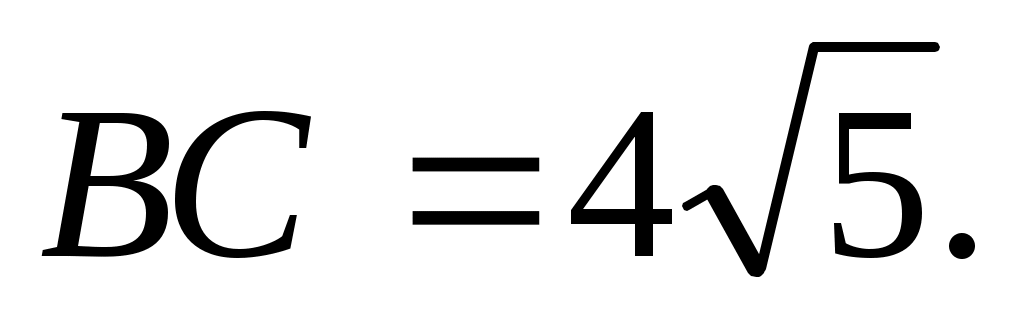
4) 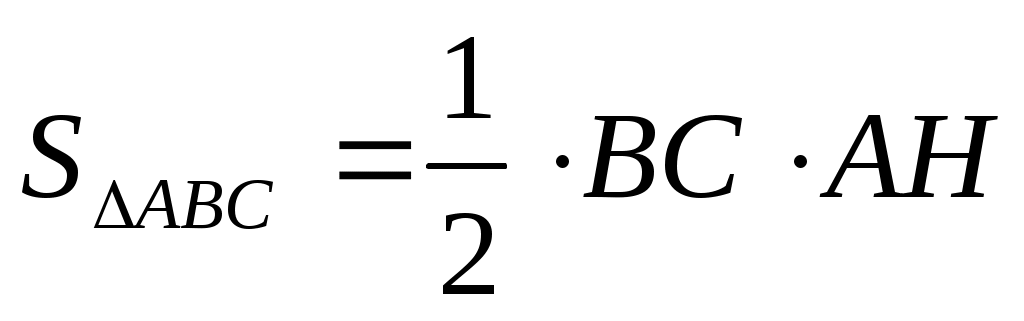 или или 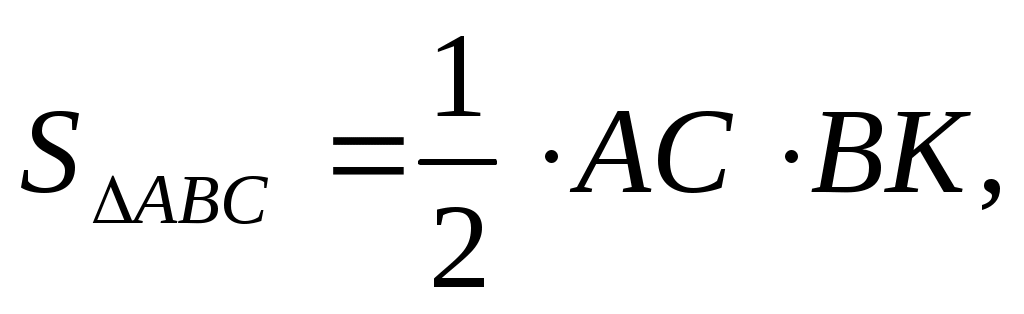 отсюда отсюда 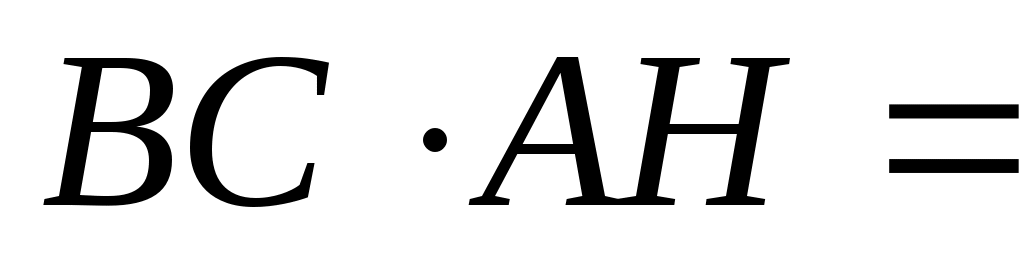 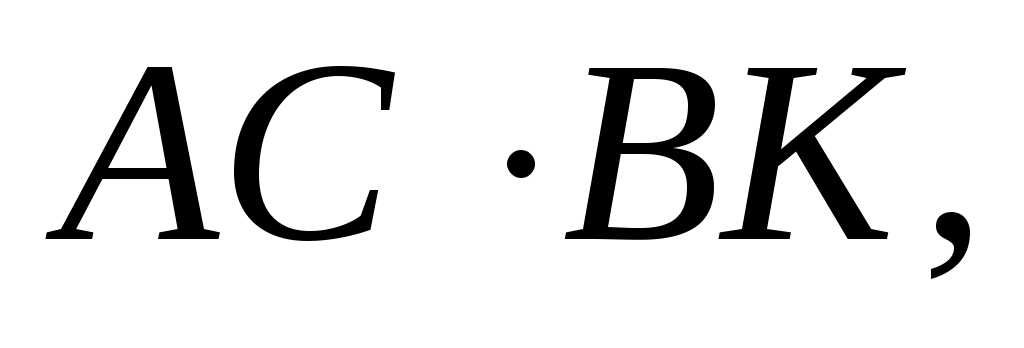
т.е. 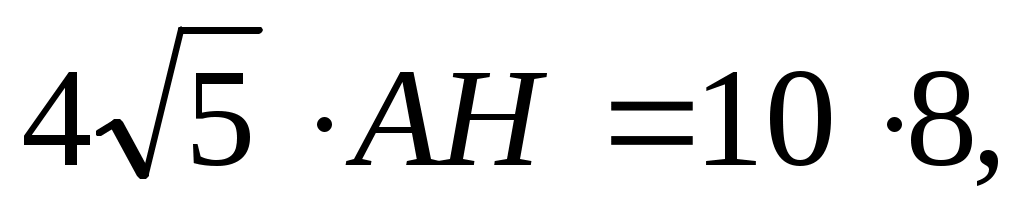 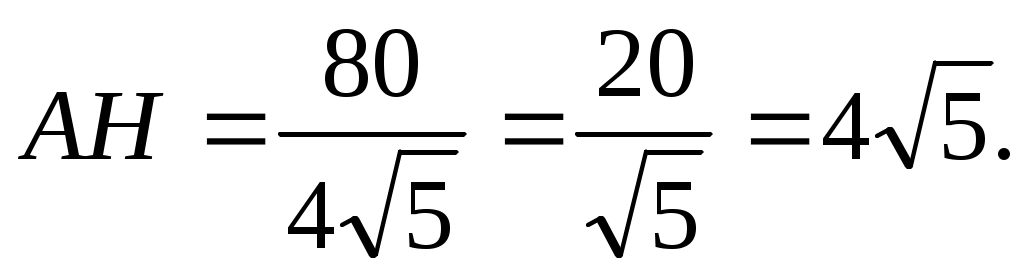 Ответ: Ответ: 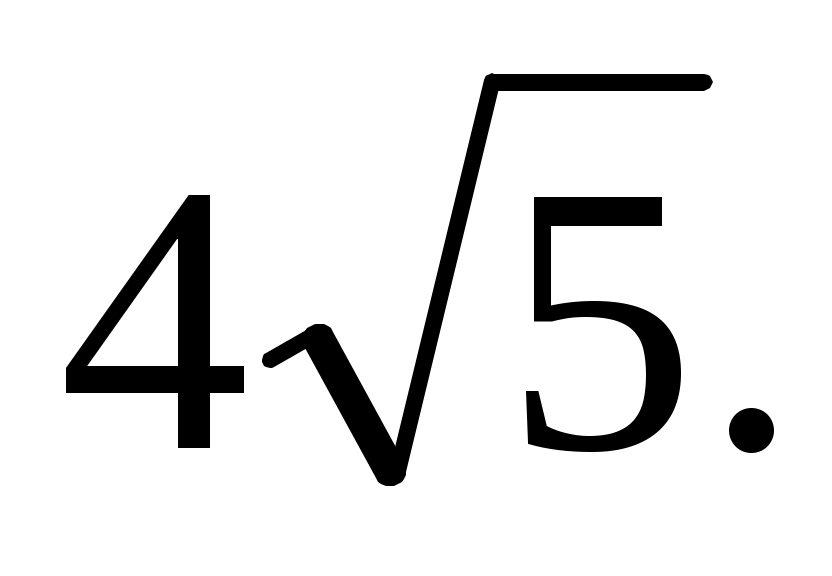
|
Задача 6. На стороне ВС треугольника АВС отмечена точка К. Известно, что  В + В + С = С =  АКВ, АК = 5, ВК = 16, КС = 2. Найдите сторону АВ. АКВ, АК = 5, ВК = 16, КС = 2. Найдите сторону АВ.
РЕШЕНИЕ.
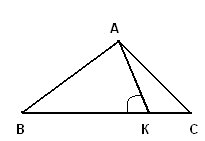
|
1)  АКВ внешний для АКВ внешний для 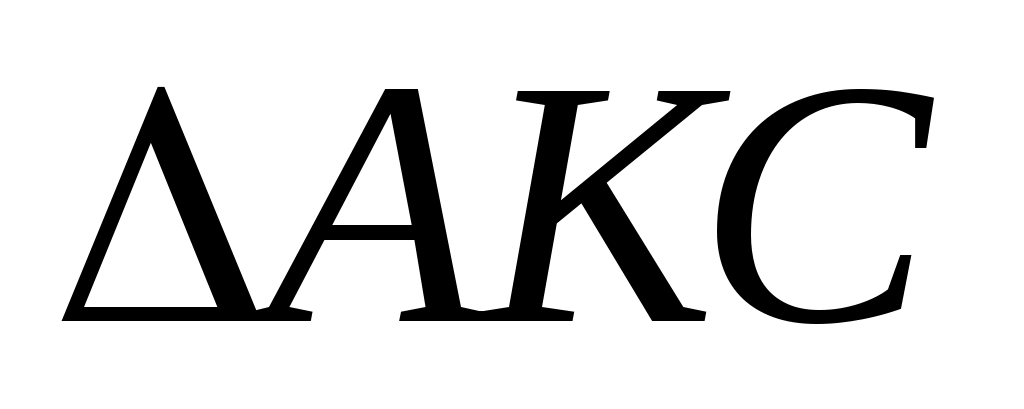 , поэтому , поэтому
 АКВ = АКВ =  КАС + КАС +  С, а по условию задачи С, а по условию задачи
 АКВ = АКВ =  В + В +  С, значит С, значит  КАС = КАС =  В. В.
2)В треугольниках АВС и КАС:  С – общий, С – общий,  КАС = КАС =  В, следовательно, они подобны. Из подобия получаем В, следовательно, они подобны. Из подобия получаем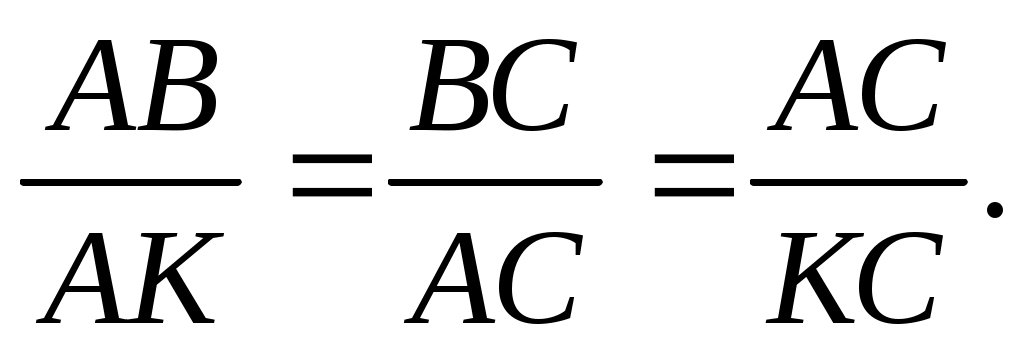
|
Из пропорции 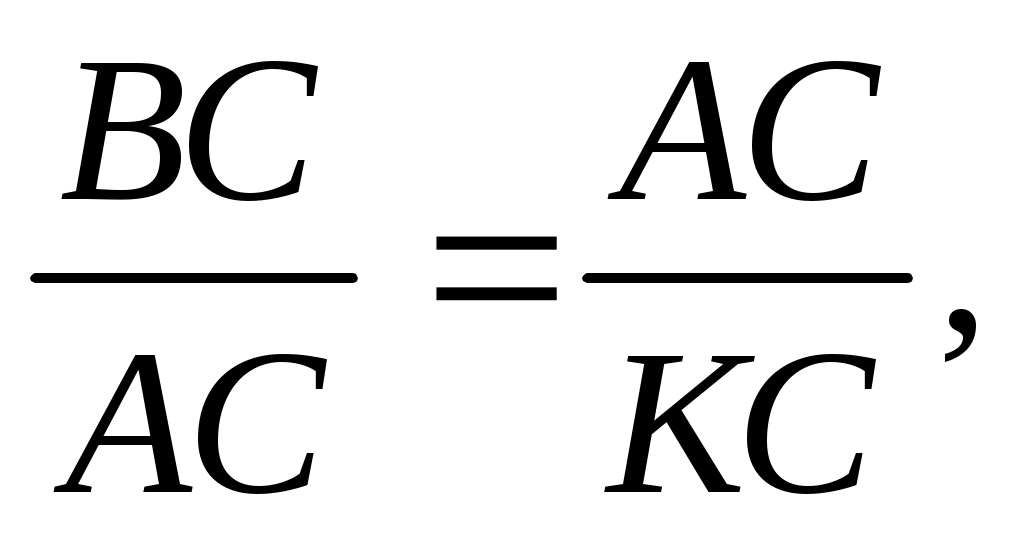 получаем получаем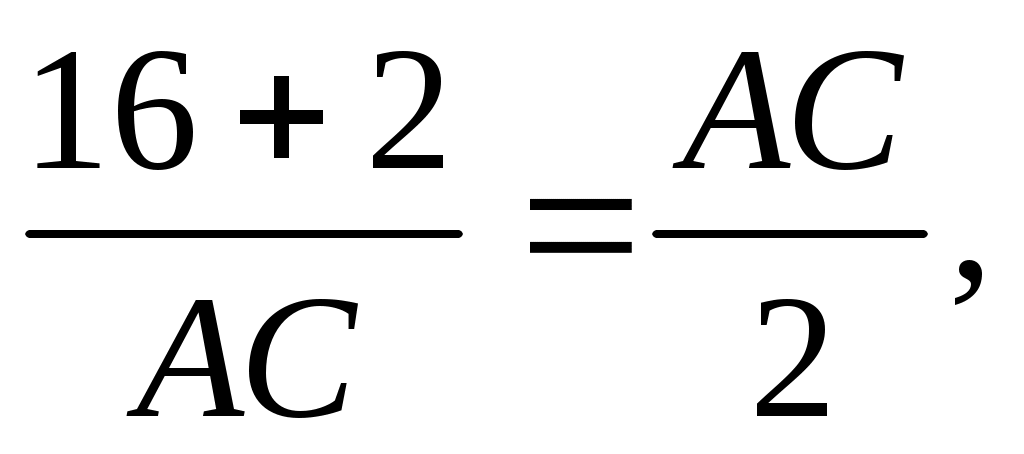 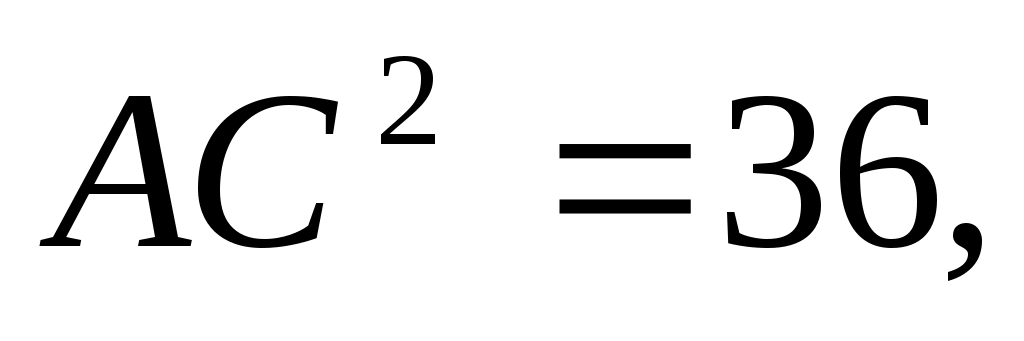 АС = 6. АС = 6.
3) Из пропорции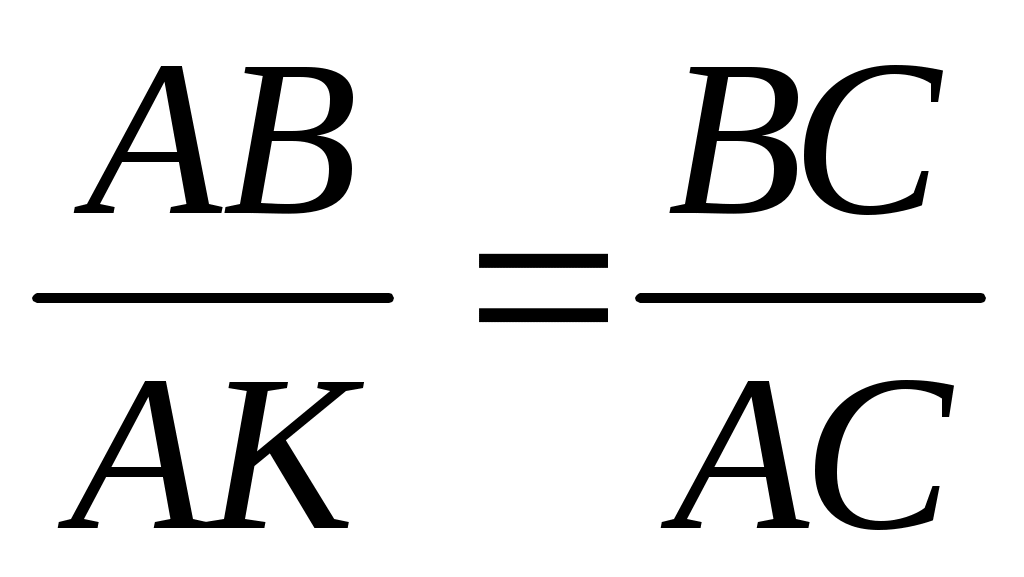 получаем получаем 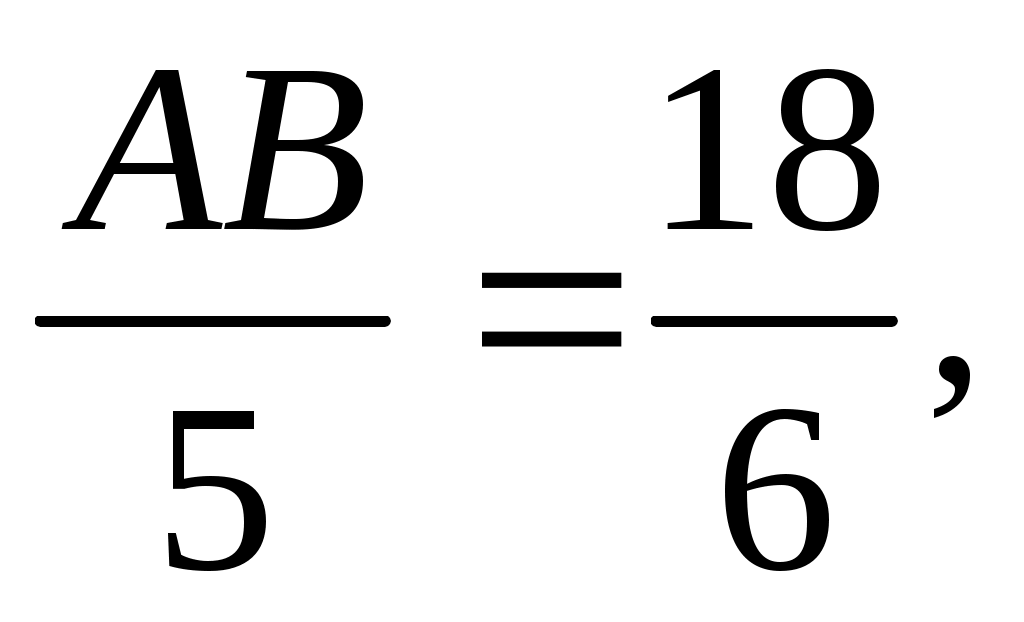 следовательно, АВ = 15. Ответ: 15. следовательно, АВ = 15. Ответ: 15.
|
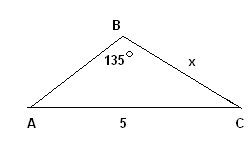
Задача 7. В треугольнике АВС  В = В = 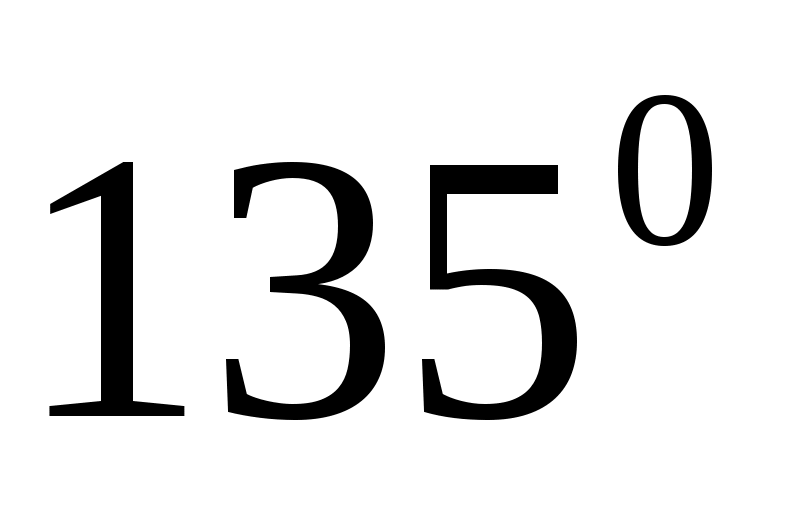 , АВ = , АВ = 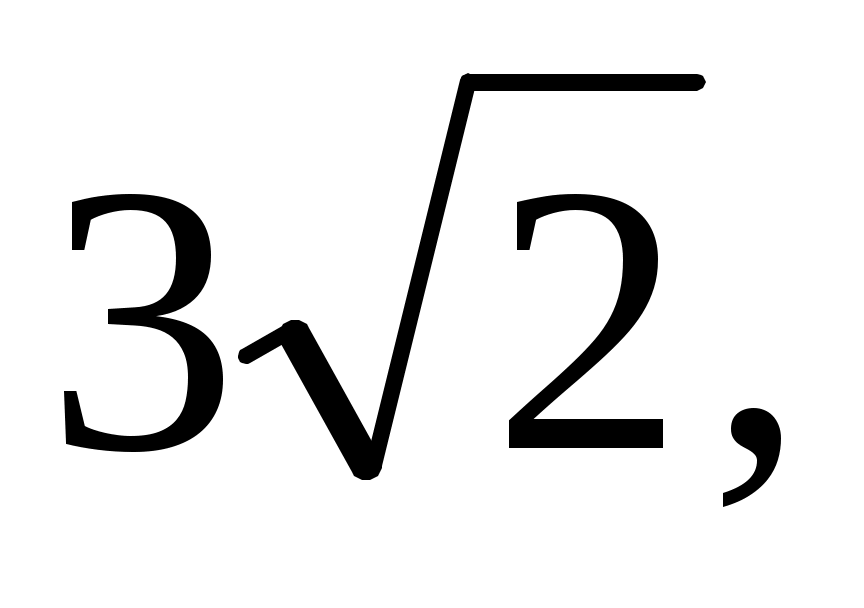 АС = 5. Найдите площадь АС = 5. Найдите площадь 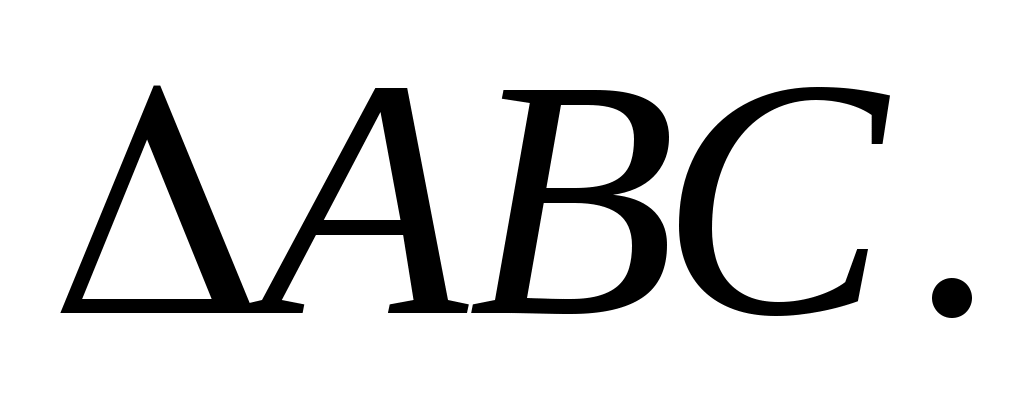
РЕШЕНИЕ.
|
1) Пусть ВС = х. По теореме косинусов получим: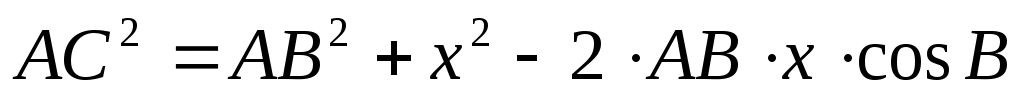 , подставим данные и получим уравнение , подставим данные и получим уравнение
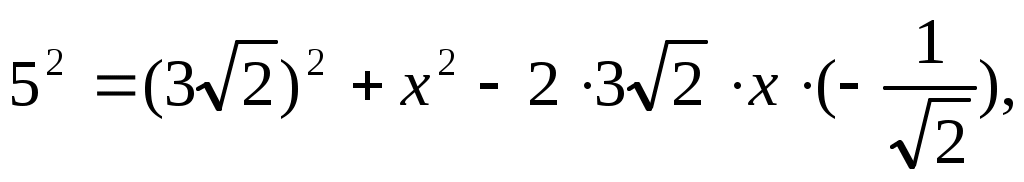 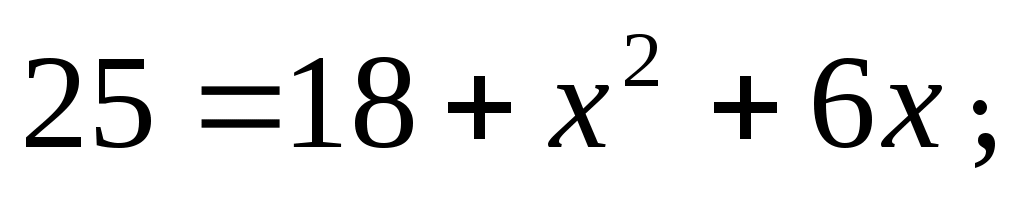 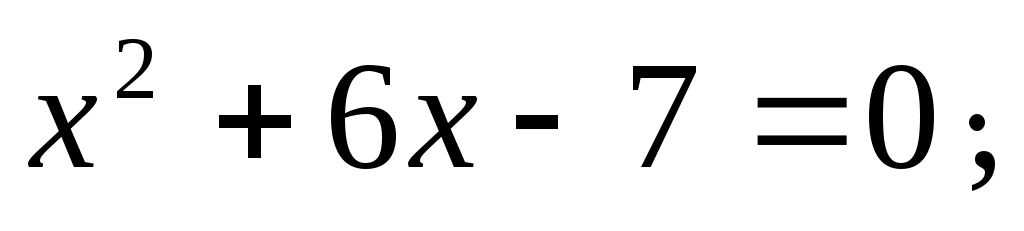 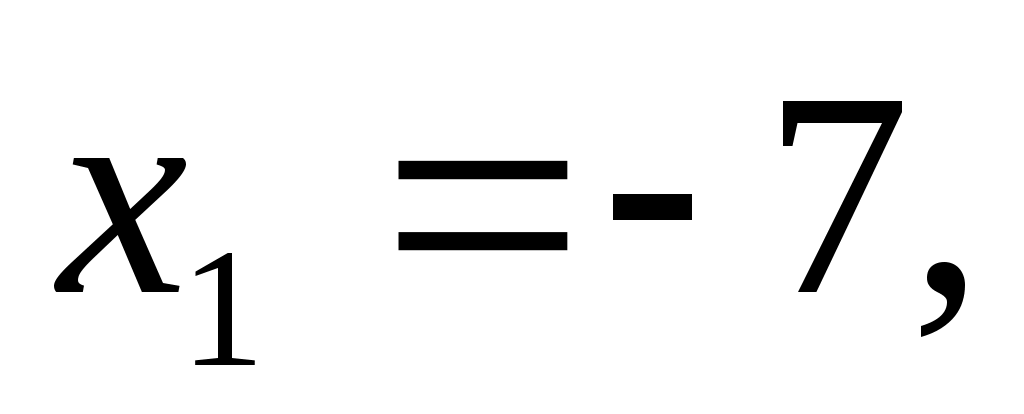 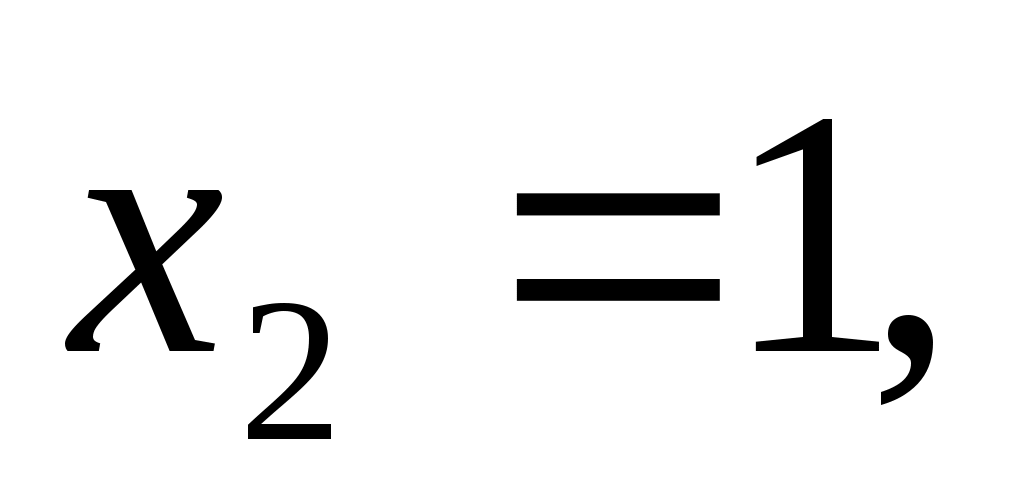
ВС = 1.
|
2) 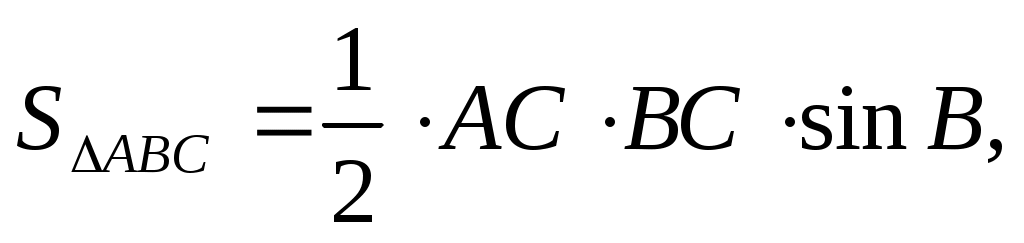 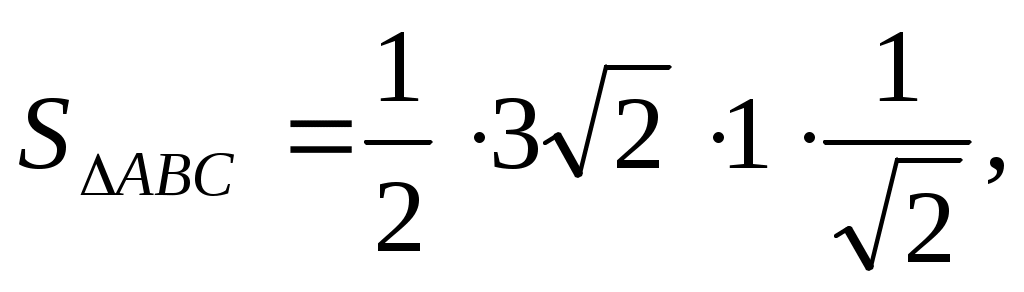 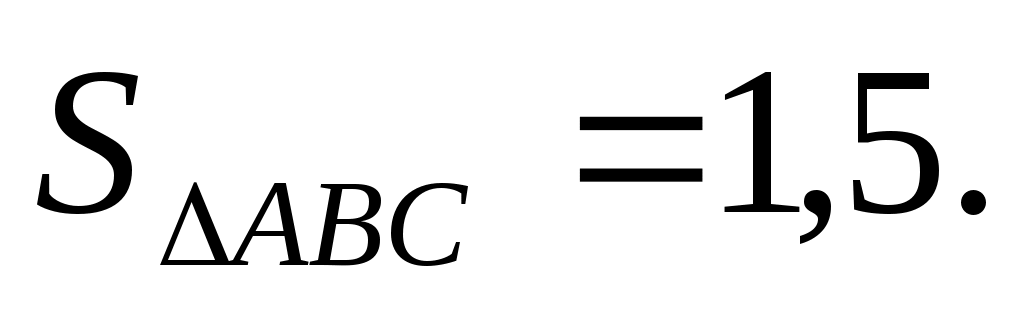
Ответ: 1,5.
|
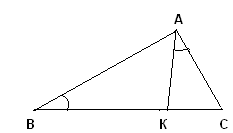
Задача 8. В треугольнике АВС сторона АВ = 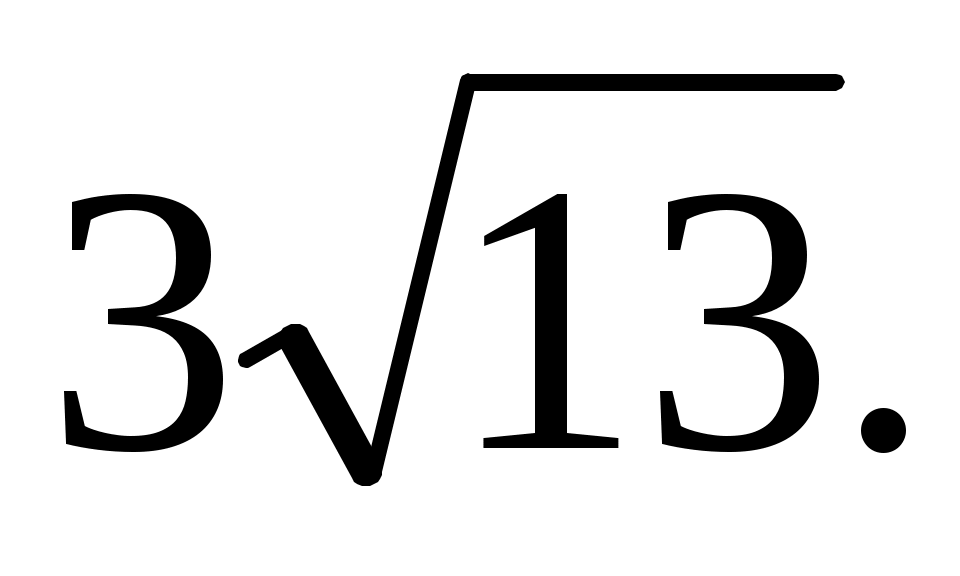 На стороне ВС отмечена точка К так, что На стороне ВС отмечена точка К так, что  КАС = КАС =  В, Найдите площадь , если ВК = 9, КС = 4. В, Найдите площадь , если ВК = 9, КС = 4.
РЕШЕНИЕ.
|
1) В 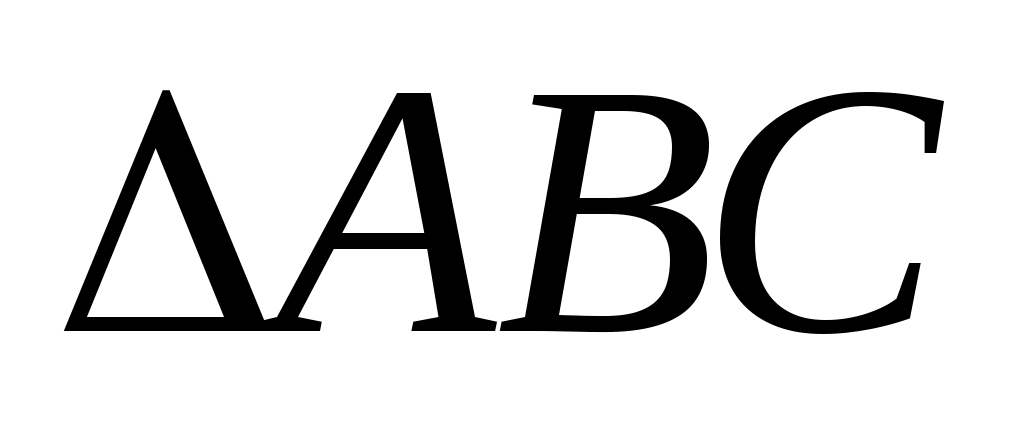 и и 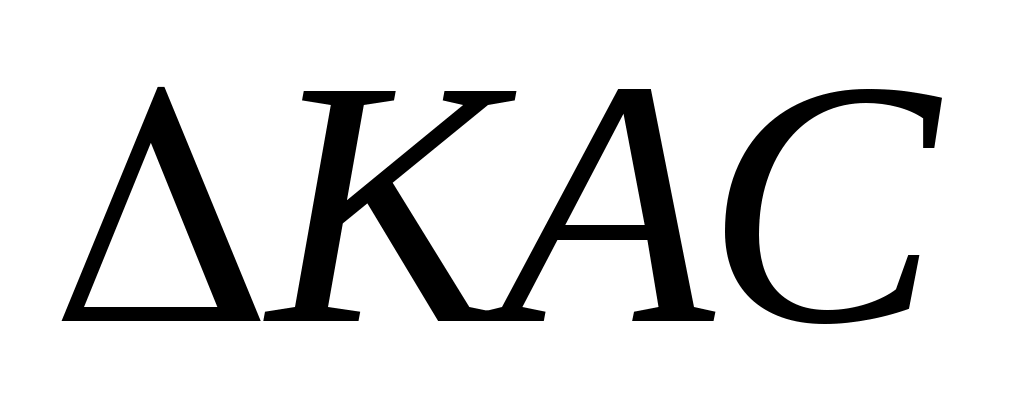 : :
 С –общий, С –общий,  В = В = КАС, следовательно, КАС, следовательно,
они подобны. Из подобия получаем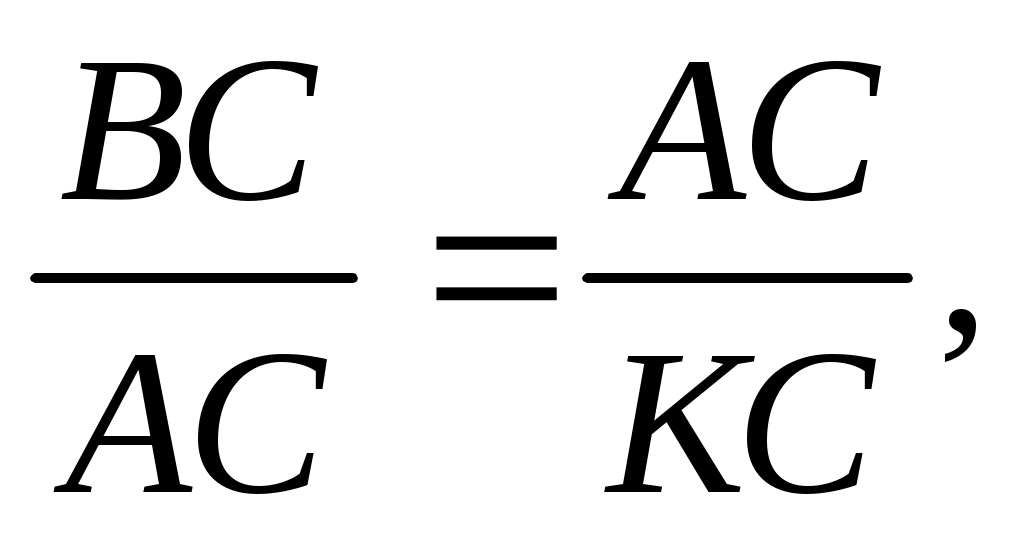 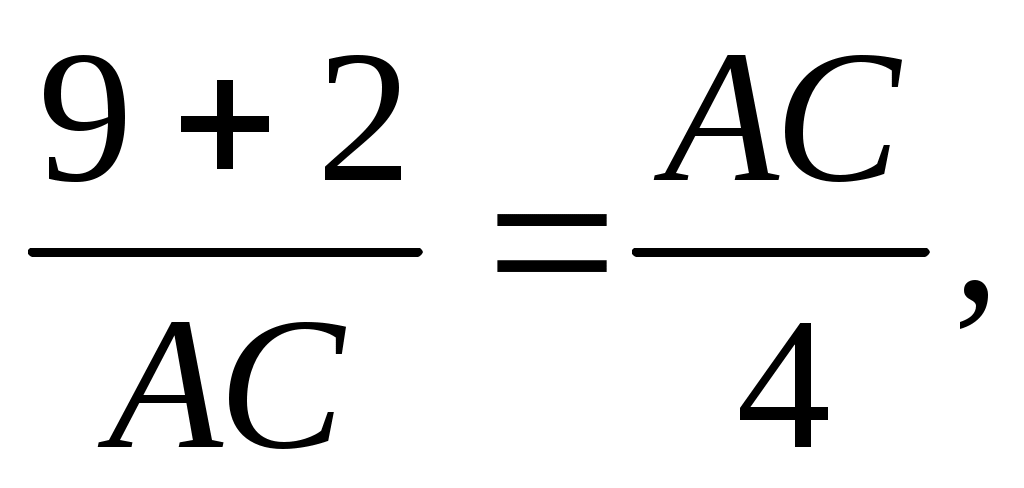 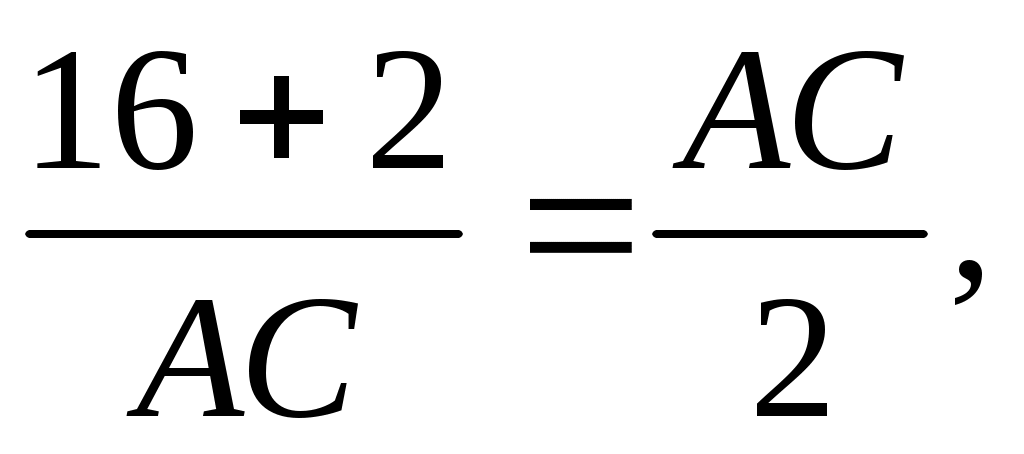
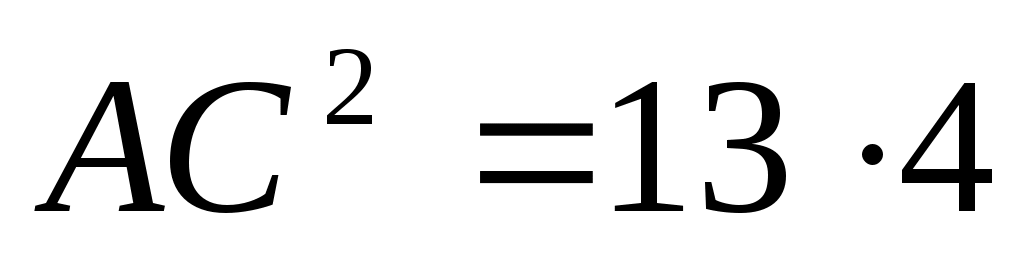 , , 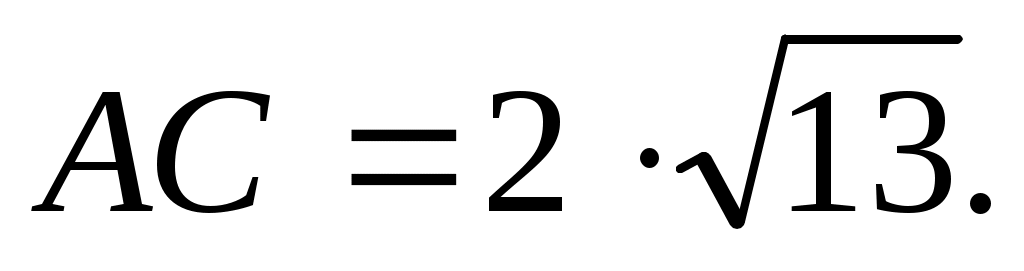
|
2)Определим вид 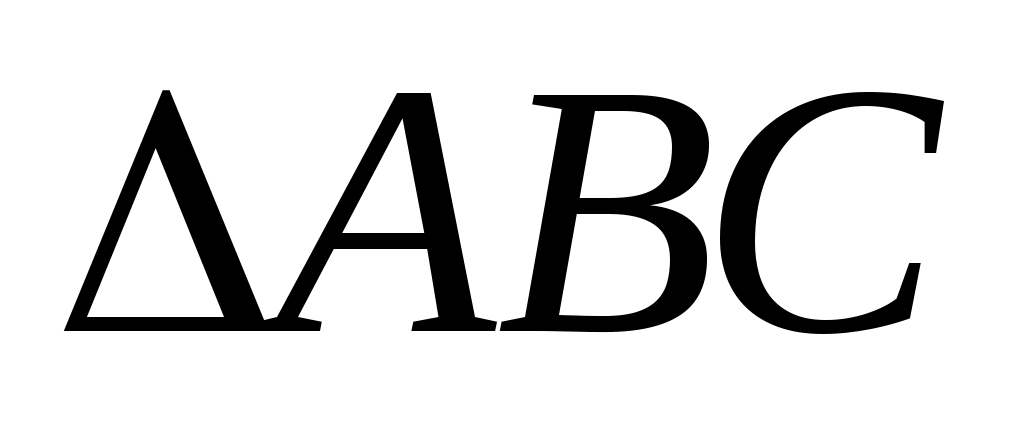 : :
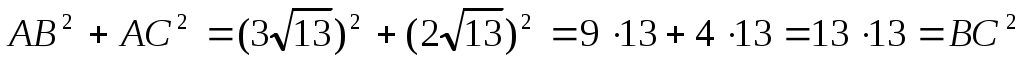 , следовательно , следовательно  прямоугольный с катетами АВ и АС. прямоугольный с катетами АВ и АС.
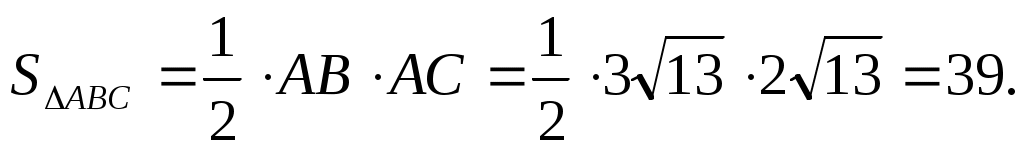 Ответ: 39. Ответ: 39.
|
Заметим, что использование формулы Герона существенно усложнило бы решение задачи.
|
 Скачать 0.8 Mb.
Скачать 0.8 Mb.







