Главная страница
Навигация по странице:

  • 2.4. Применение признаков подобия треугольников и признаков параллельности прямых Задача 19.

  • 2.5. Четырехугольники и окружность Задача 20.

  • Список литературы

    		•

    ИГЭ для Гэ. Задания по планиметрии на ЕГЭ. 6 Исторические вопросы


    Скачать 0.8 Mb.
    Название6 Исторические вопросы
    АнкорИГЭ для Гэ
    Дата20.12.2021
    Размер0.8 Mb.
    Формат файлаdoc
    Имя файлаЗадания по планиметрии на ЕГЭ.doc
    ТипДокументы
    #310971
    страница4 из 4
    1   2   3   4

    Параллелограмм

    Задача 18. В параллелограмме ABCD , биссектрисы углов В и С пересекаются в точке К, лежащей на стороне AD, СК = 3. Найдите площадь параллелограмма.

    РЕШЕНИЕ.
    1)В параллелограмме ABCD

    В = 180° - BCD == 60°. Так как СК — биссектриса угла BCD, BCK = DCK = ,

    как ВК — биссектриса угла ABC,

    ABK= СВК= . Следовательно,
    BKC = 180° - (30° + 60°) = 90°. Поэтому в

    ВСК ВС = 2КС = 6.

    2)AD║ВС, поэтому CKD = BCK = 60° (внутренние накрест лежащие). Следовательно, KCD равносторонний, поэтому CD = КС = 3. Значит, AB = CD = 3.

    3) = AB·ВС· sinB, = 3·6· sin60° = 9

    Ответ: 9

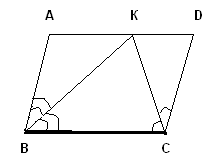
    2.4. Применение признаков подобия треугольников и признаков параллельности прямых
    Задача 19. В параллелограмме ABCD биссектриса угла D пересекает сторону AB в точке К и прямую BC в точке Р. Найдите периметр треугольника CDР, если DК = 18, РК = 24, АD = 15.

    РЕШЕНИЕ.
    1) DР = DК + КР = 24 + 18 = 42.

    Пусть РВ = х, тогда РС = х + 15.

    CDР подобен ВКР по двум углам:

    Р – общий, 2 = 4 как соответственные углы, образованные

    прямыми CD║AB и секущей DР.

    Пусть РВ = х, тогда СР = х +15.

    Из подобия треугольников получим пропорцию ;

    7х = 60 + 4х; 3х = 60, х = 20. РВ = 20, РС = 20 + 15=35.

    2) 1 = 2 т.к. DР биссектриса D

    1 = 5 – как накрест лежащие при АD║BС и секущей DР;

    Из всего этого следует, что 2 = 5, а это значит, что CDР равнобедренный с основанием DР и в нем DС = РС = 35.

    3)

    Ответ: 112.


    2.5. Четырехугольники и окружность
    Задача 20. Диагональ АС трапеции ABCD перпендикулярна боковой стороне CD. Окружность, описанная около треугольника ABC, касается прямой CD и пересекает основание AD в точке М, AM = 8, MD = 2. Найдите площадь трапеции.

    РЕШЕНИЕ.
    Так как окружность, описанная около треугольника ABC, касается прямой CD, то точка С — точка касания.

    Следовательно, радиус, проведенный в точку касания, перпендикулярен прямой CD. По условию задачи диагональ АС перпендикулярна боковой стороне CD.

    Поэтому АС — диаметр окружности, описанной около треугольника ABC. Следовательно, ABC= CMA=90°. Значит, четырехугольник АВСМ— прямоугольник. Получим также, что ВС = АМ = 8,

    Найдем площадь трапеции:

    Ответ: 36.


    Задача 21. Найдите радиус окружности, вписанной в равнобедренную трапецию, если средняя линия трапеции равна , а косинус угла при основании трапеции равен .

    РЕШЕНИЕ.



    1)Средняя линия трапеции равна

    BC + AD = 2

    2)Известно, что если окружность вписана в трапецию,

    то сумма боковых сторон трапеции равна сумме ее оснований.

    BC + AD = AB + CD, т.к. трапеция равнобокая,

    то BC + AD = 2AB = 2 , AB = .

    3) Проведем высоту BН, тогда r = BH : 2.

    Из ΔАBН : АН = АB · cos BAH, АН =

    (по теореме Пифагора).

    4) r = 3 : 2 =1,5.

    Ответ: 1,5.


    Заключение
    Анализ решаемости ЕГЭ-2010 показывает, что с задачей В4, где проверяются умения решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей) справились 74,7% российских школьников. А с задачей В6, где проверяется умение решать планиметрические задачи, моделировать реальные ситуации на языке геометрии, исследовать построенные модели с использованием геометрических понятий и теорем, справились 86,3% школьников.

    С задачей С4 результаты значительно хуже. Не справившихся - 94,2%, не приступивших к выполнению задания – 4,2%, а полностью и правильно выполнивших – 1,6%.

    Следовательно, школьникам необходимо повысить уровень знаний по разделу геометрии – Планиметрия. Решение планиметрических задач способствует углублению и обогащению математических знаний.

    Умение решать планиметрические задачи в школьном курсе математики являются очень важными, развитие которых требует значительных усилий со стороны учителя математики. Учитель сам обязан в достаточной мере владеть методиками формирования умений и навыков решать планиметрические задачи.

    Данная работа поможет подготовиться школьникам к ЕГЭ по математике.

    Список литературы


    1. Блок А. Я. Методика преподавания в школе. – М.: Просвещение, 1987.

    2. Гильберт Д. Основания геометрии. – М.: Гостехиздат, 1948.

    3. Глейзер Г. И. История математики в школе. Пособие для учителей. – М.: Просвещение, 1964.

    4. Глейзер Г.И. История математики в школе VII-VIII кл. Пособие для учителей. – М.: Просвещение, 1982. – 240с.

    5. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. Пособие для учащихся 5-6 класса. - М.: Просвещение, 1989.

    6. ЕГЭ. Математика. Эффективная подготовка. 100 баллов. Авторы Лаппо Л.Д., М.А.Попов.

    7. ЕГЭ-2006. Федеральный центр тестирования. – М., 2005.

    8. Еникеева О. Б., Крупич В. И. Учить школьников учиться математике. – М., 1990.

    9. Киселев А. И., Рыбкин Н. А. Геометрия: Планиметрия: 7-9 кл.: Учебник и задачник. – М.: Дрофа, 1995.

    10. Киселев А.П. Геометрия. / Под ред. Н.А. Глаголева. – М.: ФИЗМАТЛИТ, 2004. – 328с.

    11. Колмогоров А. Н. Математика и её историческом развитии. – М.: Наука, 1991.

    12. Лаппо Л.Д., М.А.Попов. – М. : Экзамен, 2008.

    13. Маслова Т.Н. Справочник школьника по математике. 5-11 кл. / Т.Н.Маслова, А.М.Суходский. – М.: Оникс, Мир и Образование, 2008. – 672с.

    14. Математика. Типовые тестовые задания. / Под ред. Семенова А.Л., Ященко И.В. - М.: МЦНМО, 2011. – 64с.

    15. Математический энциклопедический словарь. – М.: Советская энциклопедия, 1988.

    16. Метельский Н.В. История методики математики. – Минск: Высшая школа, 1981. -178 с.

    17. Методика обучения геометрии. / Под ред. В.А.Гусева. - М. ACADEMA, 2004-367 c.

    18. Методика преподавания математики в средней школе. Частная методика. Составитель В.И. Мишин. - М.: Просвещение. 1987-415 с.

    19. Методическое пособие для подготовки к ЕГЭ-2006. / Под ред. Т.А.Корешкова, Ю.А.Глазков, В.В.Мирошин, Н.В.Шевелева. – М.: Экзамен, 2006.

    20. Оганесян В.А., Ю.М. Колягин, Г.Л. Луканкин, В.Я. Санинский. Методика преподавания математики в средней школе. Общая методика. - М., Просвещение, 1988. - 368 с.

    21. Погорелов А. В. Геометрия 7-11. Учебник для общеобразовательных учреждений. – М.: Просвещение, 1999.

    22. Практикум по методике преподавания математики в средней школе. / Под ред. В.И. Мишина. - М.: Просвещение, 1993. - 190 с.

    23. Рыбников К. А. История математики. – М.: МГУ, 1994.

    24. Саранцев Г.И. Общая методика преподавания математики. - Саранск, 1999. - 190 с.

    25. Смирнов В.А. Геометрия. Планиметрия: Пособие для подготовки к ЕГЭ / Под ред. А.Л.Семенова, И.В.Ященко. – М.: МЦНМО, 2009. – 256с.

    26. Тематические тесты. ЕГЭ. Математика. / Под ред. Ф.Ф.Лысенко. - Ростов-н/Д: Легион, 2007.

    27. Черкасов Р.С., Столяр А.А. Методика преподавания математики. Общая методика. - М.: Просвещение, 1985. - 337 с.

    28. Чичигин В.Г. Методика преподавания геометрии. Планиметрия. – М., 1959.

    29. Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия. Учебное пособие для 5-6 классов. - Смоленск: Русич, 1995.

    30. Штейн Е.А. Большая школьная энциклопедия. Том 1; - М., 2004.

    31. Энциклопедический словарь юного математика для старшего и среднего школьного возраста. – М.: Педагогика, 1989.





    1   2   3   4

    написать администратору сайта