ИГЭ для Гэ. Задания по планиметрии на ЕГЭ. 6 Исторические вопросы
 Скачать 0.8 Mb.
|
|
Оглавление
Введение Школьный курс геометрии имеет наибольшую стройность, логическую строгость и последовательность по сравнению с другими учебными математическими предметами. Программа основного курса геометрии построена следующим образом: сначала изучается планиметрия (7-9 кл.), а затем – стереометрия (10-11 кл.). В основе этого построения лежит та система, которая была дана Евклидом в его «Началах». Можно с полной уверенностью сказать, что из всех математических дисциплин именно занятие геометрией в наибольшей мере способствует развитию интуиции и воображения, а, следовательно, способствует творческому и интеллектуальному развитию личности. Планиметрия рассматривает свойства таких фигур, все части которых помещаются на одной плоскости. Задачи по планиметрии встречаются на ЕГЭ по математике. Часто школьники не могут справиться с данными заданиями. Анализ результатов ЕГЭ показывает, что решаемость планиметрических задач на ЕГЭ довольно низкая (11,7 – 13 %), как и в предыдущие годы, участники экзамена 2010 года в целом показали невысокие результаты при решении геометрических задач базового и повышенного уровней сложности. Многие экзаменуемые вообще не приступали к решению геометрических задач не только повышенного уровня, но и базового. Эти результаты отражают ситуацию, сложившуюся в школе, которая была явно неблагоприятна в отношении изучения геометрии, как утверждает Федеральная служба по надзору в сфере образования и науки и Федеральный институт педагогических измерений, эти выводы и побудили нас на более глубокое изучение этого вопроса. Есть много разновидностей планиметрических задач. Для решения таких задач лучше знать специальные приемы их решения. В работе рассматриваются некоторые виды планиметрических задач, и при знании приведенных приемов решения, многие из них будут вполне посильными для любого школьника. Задачи такого типа входят в Единый государственный экзамен по математике. Большинство планиметрических задач, предъявляемых на ЕГЭ, можно отнести к одной из следующих тем • Треугольники; • Четырехугольники; • Окружности; • Треугольники и окружность; • Четырехугольники и окружность; • Правильные многоугольники, вписанные или описанные около окружности. С 2010 года в структуру ЕГЭ по математике внесены некоторые изменения. Исключены задачи с выбором ответа. Сокращено общее количество задач. Все задачи разбиты на две группы: B (базовые задачи) и С (задачи повышенного уровня трудности). Группа B содержит 12 задач (из них 4 геометрические). Группа С содержит 6 задач (из них 2 геометрические). Геометрические задачи на ЕГЭ по математике традиционно считаются сложными. Объект исследования – процесс изучения планиметрии в школьном курсе. Предмет исследования – процесс изучения планиметрических задач, предложенных школьникам на ЕГЭ. Цель исследования – изучить задачи из курса планиметрии, которые предлагаются школьникам на ЕГЭ. Для достижения цели в работе были поставлены следующие задачи: Проанализировать литературу по данной теме. Рассмотреть исторические вопросы по данной теме. Рассмотреть треугольники и их виды. Рассмотреть четырехугольники, изучаемые в школьном курсе математики. Рассмотреть многоугольники и их виды. Рассмотреть понятия «окружность» и «круг» и определения, связанные с данными понятиями. Рассмотреть планиметрические задачи, представленные школьникам для выполнения на ЕГЭ, и методы их решения. Гипотеза – предположим, что если изучить ряд планиметрических задач, предложенных на ЕГЭ, и методы их решения, то это повысит уровень качества решаемых планиметрических задач и позволит предвидеть ошибки и предотвратить их при решении. Структура курсовой работы: введение, две главы, заключение, список литературы из 31 источников, объем работы – 38 листов печатного текста. Глава I. Теоретические материалы по курсу геометрии. Планиметрия 1.1. Исторические вопросы Планиметрия – раздел геометрии, изучающий свойства фигур на плоскости (от лат. слова «планум» - плоскость и греч. слова «метрео» - измеряю). В конце V в. до н.э. была полностью разработана почти вся планиметрия на основе строгих доказательств. Первое систематическое изложение планиметрии впервые было дано Евклидом в его труде «Начала». В трудах Евклида «Начала», первые шесть книг были посвящены планиметрии. Планиметрия возникла раньше, чем стереометрия. А термин «планиметрия» наоборот, был образован в средние века, по образцу античного термина «стереометрия». В «Началах» Евклида, как и в курсе школьной планиметрии, речь идет о плоских углах, меньших развернутого. Такие углы вполне достаточны для построения учения о треугольниках и выпуклых многоугольниках. Все построения, которые делаются в планиметрии, выполняются в одной плоскости. При систематическом изучении школьного курса геометрии обычно начинают с изучения планиметрии, а затем приступают к изучению стереометрии, изучающей пространственные фигуры. Основными понятиями школьного курса планиметрии являются точка, прямая, плоскость и расстояние (между двумя точками или от точки до точки), а также некоторые общематематические понятия, такие, как множество, отображение множества на множество и некоторые другие. Содержание школьного курса из года в год несколько меняется, однако его ядро остаётся в целом неизменным. Планиметрия содержит: Введение (в нём дается определение понятия фигуры как множества точек, изучаются свойства расстояний, определяются понятия аксиомы, теоремы и другие понятия). Перемещения плоскости (движение), то есть преобразования плоскости, сохраняющие расстояния между точками. Параллельность. Построение треугольников. Четырёхугольники. Многоугольники и их площади. Окружность и круг. Подобие и гомотетия. Тригонометрические функции. Метрические соотношения в треугольнике. Вписанные и описанные многоугольники. Длина окружности и площадь круга. Основными геометрическими фигурами на плоскости являются точка и прямая. Основные геометрические фигуры вводятся без определений, их свойства выражаются в аксиомах планиметрии. Аксиомы – это предложения, которые воспринимаются без доказательства, а уже с помощью аксиом доказываются теоремы планиметрии. Планиметрия дает не только представление о фигурах, их свойствах, взаимном расположении, но и учит рассуждать, ставить вопросы, анализировать, делать выводы, то есть логически мыслить. При изучении планиметрии необходимо уделять внимание применению моделей. Это объясняется тем, что они помогают ученику представить форму, могут существенно повысить эффективность усвоения материала, развить пространственное мышление, а также служить развитию и поддержанию интереса к предмету. 1.2. Треугольники и их виды Треугольник – это многоугольник с тремя сторонами или замкнутая ломаная линия из трех звеньев. Стороны и углы треугольника называются его элементами. Разделяют две классификации треугольников: по углам и по сторонам. Классификация треугольников по углам: Остроугольный треугольник – треугольник, в котором все углы острые. Прямоугольный треугольник – треугольник, в котором один из углов прямой. Тупоугольный треугольник – треугольник, в котором один из углов тупой. 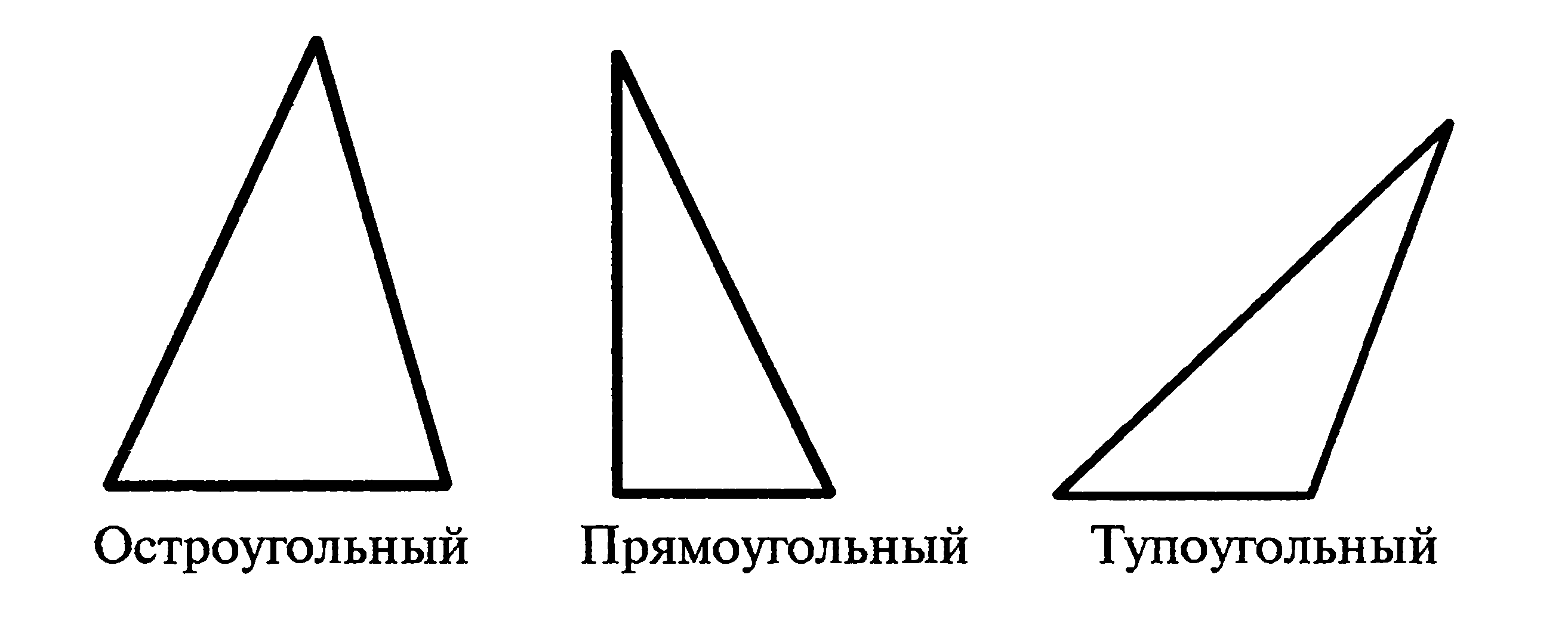 Рис.1. Классификация треугольников по углам Классификация треугольников по сторонам: Разносторонний треугольник – треугольник, в котором все стороны имеют различные длины. Равнобедренный треугольник – треугольник, в котором две стороны равны. Равносторонний треугольник – треугольник, в котором все стороны равны. 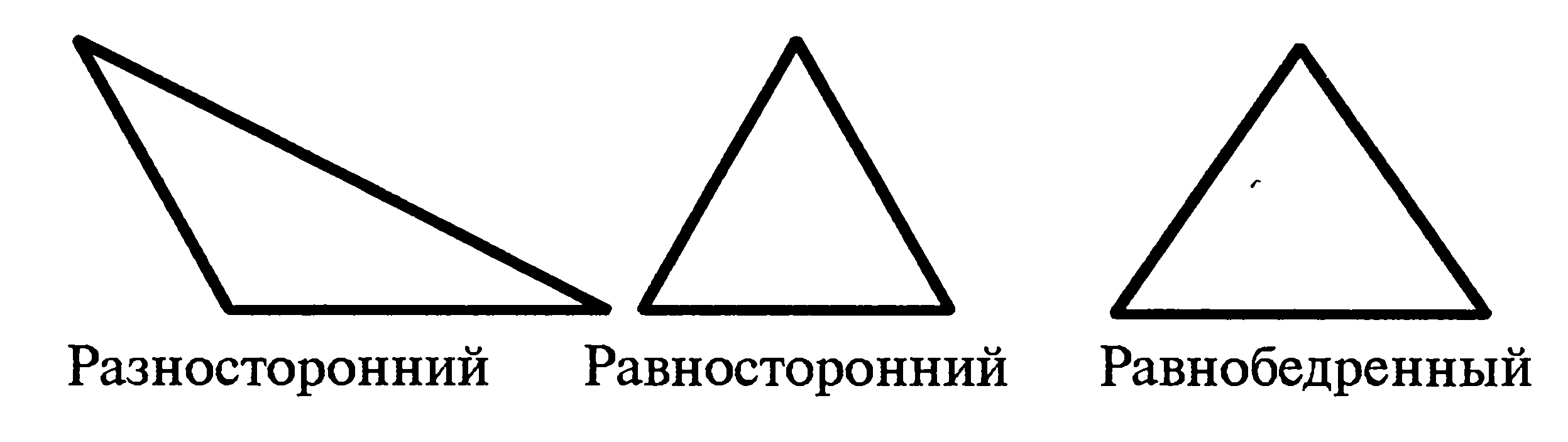 Рис.2. Классификация треугольников по сторонам Соотношение между сторонами и углами треугольника: Против большей стороны лежит больший угол. Против равных сторон лежат равные углы. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними (теорема косинусов). Стороны треугольника пропорциональны синусам противолежащих углов (теорема синусов). Свойства углов треугольника: Сумма углов любого треугольника равна 1800. Внешний угол любого треугольника равен сумме двух внутренних углов, не смежных с ним. В равнобедренном треугольнике углы при основании равны. В прямоугольном треугольнике сумма острых углов равна 900. Основные линии треугольника Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны этого треугольника. Свойства медиан треугольника Медиана разбивает треугольник на два треугольника одинаковой площади. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника. Весь треугольник разделяется своими медианами на шесть равновеликих треугольников. Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника. Свойства биссектрис треугольника Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла. Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилегажащим сторонам. Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник. Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника. Свойства высот треугольника В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному. В остроугольном треугольнике две его высоты отсекают от него подобные треугольники. Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром к отрезку. Свойства серединных перпендикуляров треугольника Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему. Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника. Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. Свойство средней линии треугольника Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. Признаки равенства прямоугольных треугольников Два прямоугольных треугольника равны, если у них соответственно равны: гипотенуза и острый угол; катет и противолежащий угол; катет и прилежащий угол; два катета; гипотенуза и катет. Подобие треугольников Два треугольника подобны, если выполняется одно из следующих условий, называемых признаками подобия: два угла одного треугольника равны двум углам другого треугольника; две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами, равны; три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника. В подобных треугольниках соответствующие линии (высоты, медианы, биссектрисы и т. п.) пропорциональны. Площадь треугольника вычисляется: 1)  2)  3)  ,  Формула Герона.Задачи по этой теме проверяют: знание свойств различных видов треугольников (свойства медиан, биссектрис и высот); умение вычислять элементы прямоугольного треугольника, используя теорему Пифагора и тригонометрические функции острого угла; умение применять теорему косинусов и теорему синусов для вычисления элементов косоугольных треугольников; умение применять признаки подобия треугольников и вычислять элементы подобных треугольников; умение вычислять площадь треугольника разными способами. 1.3. Четырехугольники Четырёхугольник — это многоугольник, содержащий четыре вершины и четыре стороны. Различают выпуклые и невыпуклые четырёхугольники. 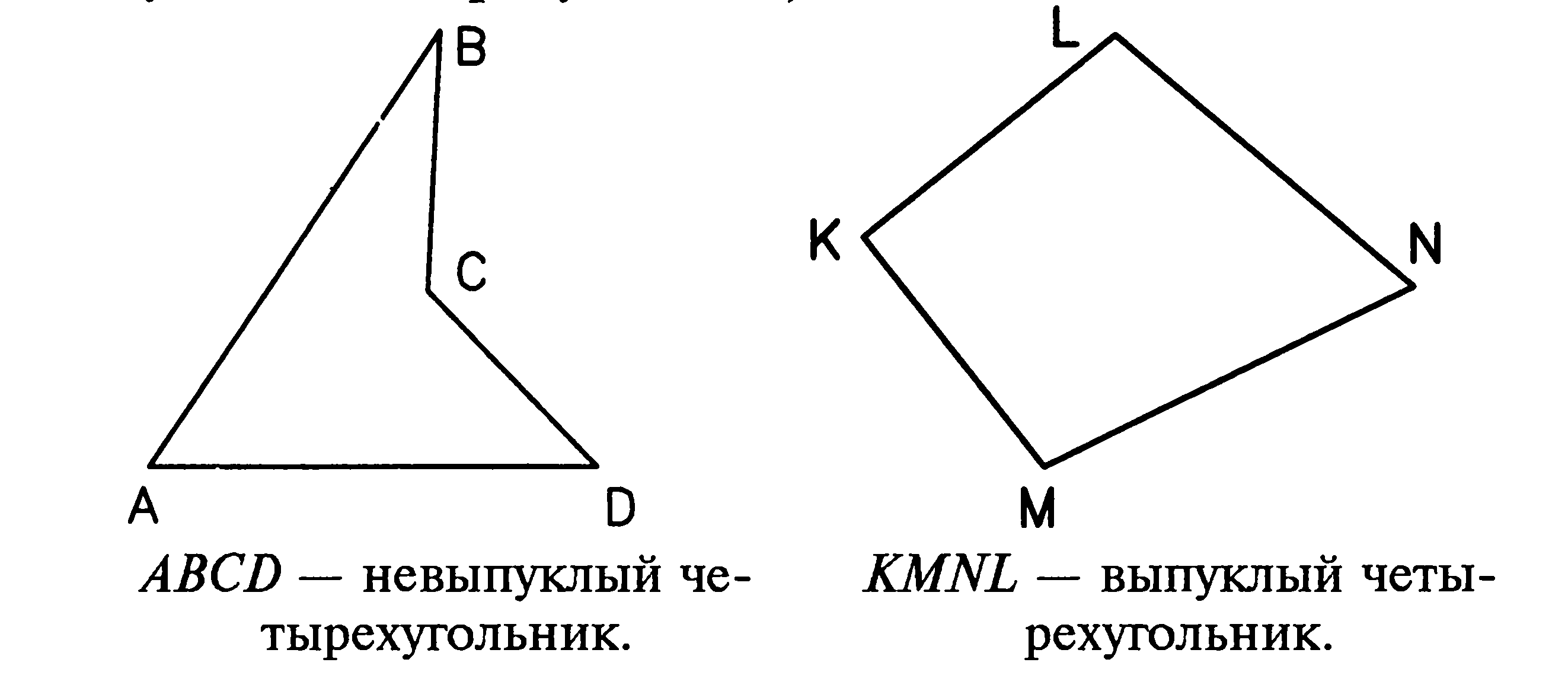 Рис.3. Выпуклые и невыпуклые четырехугольники В школьном курсе математики изучаются только выпуклые четырехугольники, которые для краткости называют просто четырехугольниками. Стороны четырехугольника, имеющие общую вершину, называются соседними. Стороны четырехугольника, не имеющие общих вершин, называются противоположными. Отрезки, соединяющие противоположные вершины, называются диагоналями. Четырехугольник имеет две диагонали. Сумма внутренних углов четырехугольника равна 3600, и сумма внешних углов равна 3600. Периметром четырехугольника называется сумма длин его сторон. Частными случаями четырехугольников являются квадрат, прямоугольник, параллелограмм, ромб, трапеция. Виды четырёхугольников 1. Параллелограмм — четырёхугольник, у которого все противоположные стороны параллельны; Прямоугольник — четырёхугольник, у которого все углы прямые; Ромб — четырёхугольник, у которого все стороны равны; Квадрат — четырёхугольник, у которого все углы прямые и все стороны равны; 2. Трапеция — четырёхугольник, у которого две противоположные стороны параллельны. Четырехугольник, все вершины которого принадлежат окружности, называется вписанным в эту окружность, а окружность – описанной около этого четырехугольника. Около четырехугольника можно описать окружность тогда и только тогда, когда сумма противолежащих углов этого четырехугольника равна 1800. Следовательно, параллелограмм можно вписать в окружность, если он является прямоугольником или квадратом. Трапецию можно вписать в окружность, если она является равнобедренной. Некоторые специфические свойства трапеции: В равнобедренной трапеции высота, проведенная из вершины меньшего основания, разбивает большее основание на отрезки, равные полусумме и полуразности оснований. Биссектрисы углов, прилежащих к боковой стороне трапеции, перпендикулярны. Площадь трапеции равна произведению ее средней линии на высоту. Полезные свойства параллелограмма:  , где и  диагонали параллелограмма, а  - угол между диагоналями (отметим также, что эта формула справедлива для любого выпуклого четырехугольника);Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник В параллелограмме биссектрисы углов, прилежащих к одной стороне, перпендикулярны. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон. В параллелограмме равны площади всех четырех треугольников, на которые он разбивается диагоналями. И  нтересный геометрический факт: если последовательно соединить середины сторон произвольного четырехугольника, то получим параллелограмм.Если четырехугольник ABCD можно вписать в окружность, то произведение диагоналей этого четырехугольника равно сумме произведений его противоположных сторон, т.е.  Рис.4. Четырехугольник, вписанный в окружность Ч  етырехугольник, все стороны которого касаются окружности, называется описанным около окружности, а окружность называется вписанной в этот четырехугольник. В четырехугольник можно вписать окружность тогда и только тогда, когда сумму противоположных сторон этого четырехугольника равны.Рис.5. Четырехугольник, описанный около окружности  Следовательно, из всех параллелограммов лишь в ромб и квадрат можно вписать окружность. Центр окружности, вписанной в ромб или квадрат, лежит в точке пересечения диагоналей ромба или квадрата. 1.4. Многоугольники Термин «многоугольник» понимается в математике и, в частности, в школьном курсе математики двояко. Во-первых, многоугольник как линия. В этом случае многоугольник – это простая (т. е. без самопересечения) замкнутая ломаная, лежащая в некоторой плоскости. И, во-вторых, многоугольник, как часть плоскости, ограниченная простой замкнутой ломанной. Эти две трактовки понятия «многоугольник» могут быть использованы самостоятельно в зависимости от характера рассматриваемой задачи. В логическом плане второе понимание термина «многоугольник» связано с первой теоремой Жордана. В теореме Жордана речь идёт о многоугольнике как о простой замкнутой ломаной. Многоугольник – часть плоскости, ограниченная простой замкнутой ломаной. Звенья этой ломаной называются сторонами многоугольника, а ее вершины – вершинами многоугольника. Отрезки, соединяющие несоседние вершины многоугольника, называются диагоналями многоугольника. Многоугольники характеризуются углами, которые составляет каждая пара отрезков (звеньев) замкнутой ломаной, имеющих одну общую точку, и количеством отрезков (звеньев) ломаной линии. Количество отрезков (звеньев) замкнутой ломаной линии и количество углов в каждом многоугольнике совпадают. Выпуклый многоугольник – многоугольник, содержащий целиком отрезок, соединяющий две любые точки многоугольника. От количества углов многоугольника зависит его название. Три угла – треугольник, четыре – четырехугольник, пять – пятиугольник и т.д. Выпуклый многоугольник называется правильным, если все стороны и углы его равны. Расстояние от центра правильного многоугольника до какой-либо его стороны равно радиусу вписанной в него окружности. Около всякого правильного многоугольника можно описать окружность и в него вписать окружность, причем центры этих окружностей совпадают. Построение правильного многоугольника с n сторонами оставалось проблемой для математиков вплоть до XIX века. Такое построение идентично разделению окружности на n равных частей, так как, соединив между собой точки, делящие окружность на части, можно получить искомый многоугольник. Правильный четырёхугольник – это квадрат; правильный треугольник – равносторонний треугольник. Каждый угол правильного многоугольника равен 180º  , где n – число его углов.Центром правильного многоугольника называется точка, равноудаленная от всех его вершин и всех его сторон. Центральным углом правильного многоугольника называется угол, под которым видна сторона из его центра. Сумма внутренних углов многоугольника находится по формуле:  Сумма внешних углов многоугольника равна  , если брать по одному углу при каждой вершине.Ч  исло диагоналей выпуклого многоугольника можно определить по формуле:  .Рис.6. Виды правильных многоугольников 1.5. Окружность и круг 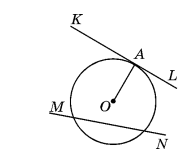 Окружностью называется геометрическое место точек, одинаково удаленных от данной точки О, называемой центром окружности. Расстояние от точки окружности до ее центра называется радиусом окружности. Рис.7. Окружность Окружность делит плоскость на две части: внутреннюю по отношению окружности и внешнюю. Внутренняя часть, включая и контур, ее ограничивающий, т.е. окружность, называется кругом. Все точки круга удалены от центра на расстояние, не большее чем радиус окружности. Внешняя часть состоит из точек, удаленных от центра на расстояние, превышающее радиус. Прямая, лежащая в той же плоскости, что и окружность, может не иметь с окружностью общих точек, может пересекать окружность в двух точках (такая прямая называется секущей) и может иметь с окружностью одну общую точку (такая прямая называется касательной). Отрезок секущей, заключенный внутри окружности, называется хордой. Перпендикуляр, опущенный на хорду из центра окружности, делит эту хорду пополам. Хорда, проходящая через центр окружности, называется диаметром. Все диаметры равны между собой и равны удвоенному радиусу. Хорда разбивает круг на две части, называемые сегментами. Если хорда совпадает с диаметром, то эти сегменты превращаются в полукруги. Справедливы следующие утверждения: Равные хорды стягивают равные дуги. Равные дуги стягиваются равными хордами. Хорды, одинаково удаленные от центра, равны. Равные хорды одинаково удалены от центра. Всякий диаметр является осью симметрии окружности и делит ее на две равные полуокружности. Итак, в данной главе мы рассмотрели вопросы теории, знание которых необходимо при решении задачи из курса планиметрии. |