Конспект урока геометрии по теме_ «Первый признак подобия треуго. Первый признак подобия треугольников
 Скачать 446.5 Kb. Скачать 446.5 Kb.
|
|
8 класс ГЕОМЕТРИЯ Урок № 36 Тема: Первый признак подобия треугольников. Тип: Урок изучения нового материала. Цели урока: Обучающие: рассмотреть первый признак подобия треугольников; сформировать у учащихся навыки применения первого признака при решении задач; закрепить знания, умения и навыки учащихся по теме «Определение подобных треугольников, отношение их площадей» в процессе решения задач. Развивающие: развитие умения правильно оперировать полученными знаниями, логически мыслить; развитие интеллектуальных умений; развитие умения принимать решения; развивать умение математически и графически оформлять результаты деятельности. Воспитательные: воспитание познавательного интереса к геометрии; воспитание самостоятельности при решении учебных задач; воспитание дисциплинированности и организованности. Подготовил: Попов Дмитрий Сергеевич. ХОД УРОКА I. Организационный момент – Здравствуйте, ребята! Проверяю готовность к уроку. – Кто сегодня в классе дежурный? Продолжаю диалог с дежурным: – Кто сегодня отсутствует? II. Проверка домашнего задания – Возникли ли у вас вопросы по выполнению домашнего задания? Если да, тогда какие? Учитель берёт на проверку 2 – 3 тетради. III. Подготовка к изучению нового материала. Актуализация опорных знаний 1. Теоретический опрос Вызываю ученика к доске и прошу доказать теорему об отношении площадей подобных треугольников. 2. Решение задач для подготовки учащихся к восприятию нового материала Учащимся выдаются карточки для решения задач:
Ответы к карточкам: I ВАРИАНТ: а) BD = 2 см, CD = 4 см; б) 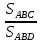 = = 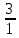 . .II ВАРИАНТ: а) SСMN = 3 см2; б) SАKN = 13,5 см2; в) SBKNM = 19,5 см2. IV. Работа по теме урока – Сформулируйте признаки равенства треугольников. – Как вы думаете существуют ли признаки подобия треугольников? – Существует утвержение, согласно которому, если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны. – Данное утверждение является первым признаком подобия треугольников и требует доказательства. Первый признак подобия треугольников На доске и в тетрадях рисунки и запись: 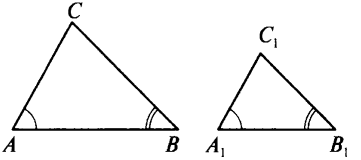 Дано: ΔАВС, ΔА1В1С1, ∠А = ∠А1, ∠В = ∠В1. Доказать: ΔАВС  ΔА1В1С1. ΔА1В1С1.Доказательство 1) ∠С = 180° – (∠А + ∠В) = 180° - (∠А1 + ∠В1) = ∠С1. 2) ∠А = ∠А1, тогда 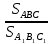 = = 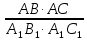 (1). (1).3) ∠C = ∠C1, тогда 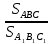 = = 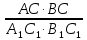 (2). (2). 4) Из (1) и (2) следует АВ : А1В1 = ВС : В1С1 (3). 5) Так как ∠А = ∠А1 ∠В = ∠В1, то ВС : В1С1 = СА : С1А1 (4). 6) Из (3) и (4) следует 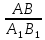 = = 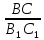 = = 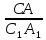 , то ΔАВС , то ΔАВС  ΔА1В1С1. ΔА1В1С1.Первый признак подобия треугольников часто называют признаком подобия треугольников по двум углам. V. Закрепление изученного материала 1. Работа по карточкам Учащимся раздаются карточки для самостоятельного решения задач.
Учитель собирает тетр 2. Решение задачпо учебнику Учащиеся самостоятельно решают № 551 (а). Учитель предлагает план решения задачи №551 (а): 1) Доказать, что ΔAED  ΔFEC. ΔFEC.2) Найти сходственные стороны этих треугольников и коэффициент подобия. 3) Найти EF и FC. Наводящие вопросы к задаче: – Что можно сказать о треугольниках AED и FEC? – Как найти коэффициент подобия этих треугольников? Краткое решение: 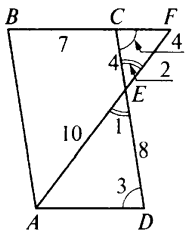 ΔAED  ΔFEC (∠1 = ∠2 как вертикальные, ΔFEC (∠1 = ∠2 как вертикальные, ∠3 = ∠4, т.к. ВС 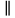 AD) AD) 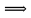 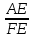 = = 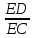 = = 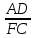 . Т.к. . Т.к. 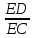 = = 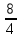 = 2, = 2,то k= 2 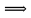 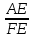 = 2 и FE = = 2 и FE = 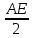 = 5 см. = 5 см. 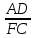 = 2 и = 2 и 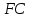 = = 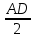 = 3,5 см. = 3,5 см.Ответ: FС = 3,5 см, EF = 5 см. Учитель вызывает более подготовленного ученика для решения задачи №555(а). VI. Рефлексия учебной деятельности Провожу теоретический опрос: – Какие треугольники называются подобными? – Сформулируйте свойство биссектрисы треугольника. – Сформулируйте теорему об отношении площаде й подобных треугольников. – Сформулируйте первый признак подобия треугольников. VII. Анонс домашнего задания Прочитать пункт 61 Выучить и научиться доказывать первый признак подобия треугольников Решить № 550, 551 (б), 553. VIII. Подведение итогов урока Учитель выставляет оценки, тем самым подводит итоги урока. |


 C Дано: ΔАВС,
C Дано: ΔАВС,
 D Найти:
D Найти:
 а) BD, CD;
а) BD, CD;
 BM : MC = 2 : 1,
BM : MC = 2 : 1,
 Найти:
Найти:
