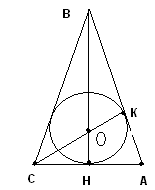ИГЭ для Гэ. Задания по планиметрии на ЕГЭ. 6 Исторические вопросы

• Название: 6 Исторические вопросы
• Анкор: ИГЭ для Гэ
• Дата: 20.12.2021
• Размер: 0.8 Mb.
• Имя файла: Задания по планиметрии на ЕГЭ.doc
• Тип: Документы; #310971
• страница: 3 из 4

2.2. Задачи на треугольники и окружности
Окружность, вписанная в треугольник.

Значительную долю задач, составляли задачи, связанные с окружностью, вписанной в тре­угольник - произвольный, равнобед­ренный или прямоугольный. В этих конфигурациях существенным момен­том является то, что окружность, впи­санная в треугольник (или в многоугольник), касается всех его сторон.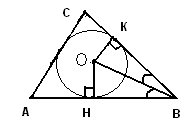



Отсюда, опираясь на свойства каса­тельных, можно получить три важней­ших для решения многих задач факта.

• 
  отрезок, соединяющий центр ок­ружности и точку ее касания со стороной, перпендикулярен этой стороне и является радиусом окружности;
  
• 
  где
  
• 
  отрезки двух соседних сторон от общей вершины до точек касания равны между собой;
  
• 
  центр вписанной окружности лежит на биссектрисе угла, образо­ванного его сторонами.
  

Использование этих четырех фактов (особенно двух последних) являлось ключевым моментом при решении задач на вписанные окружности. Рассмотрим это далее более подробно на конкрет­ных примерах.

Как показывают результаты выполнения работ, значитель­ные затруднения вызвали задачи, при решении которых нужно было использовать тот факт, что центр вписанной в треуголь­ник окружности лежит на его биссектрисе. Приведем примеры геометрических заданий и дадим комментарии к их выпол­нению.
Задача 9. В равнобедренный треугольник ABC с основани­ем АС вписана окружность с центром О. Луч СО пересекает сто­рону АВ в точке К, причем АК = 6, ВК = 12. Найдите периметр треугольника.

РЕШЕНИЕ.

	1)Для решения этой задачи требуется установить, что СК — биссектриса треугольника (это следует из того, что по условию СК проходит через центр вписанной окруж­ности). После этого, используя свойство биссектрисы треугольника, можно составить пропорцию АС = 9
2) ; Ответ: 45.

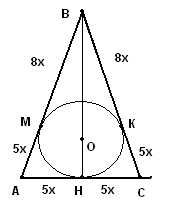
Рассмотрим одну из задач, в решении которых требовалось использовать свойство отрезков касательных.

Задача 10. Окружность с цент­ром О, вписанная в равнобедренный треугольник ABC с основанием АС, касается стороны ВС в точке К, причем СК : ВК = 5 : 8. Найдите пло­щадь треугольника, если его пери­метр равен 72.

РЕШЕНИЕ.

	1) Обозначим буквами М и Н точ­ки касания вписанной окружности со сторонами АВ и АС. Если считать ВК = 8х и СК = 5х, то АВ = ВС = 13х. Используя свойст­во отрезков касательных и то, что Н - середина основания, имеем: АМ = АН = НC = СК = 5х.
2) Из условия х =2; АС = 20, АВ = ВС = 26. 3) Найдем по формуле Герона. . = = = 240. Ответ: 240. P.S. Можно , а найти из АВН по теореме Пифагора

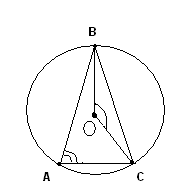
Окружность, описанная около треугольника.

Следующую группу задач составляли задачи, в которых окружность была описана около треугольника. Поскольку в этом случае стороны треугольника являются хордами окружности, а углы треуголь­ника — вписанными углами, то при решении задач использу­ются:

• 
  свойства вписанных и центральных углов;
  
• 
  свойство отрезков двух пересекающихся хорд;
  
• 
  расположение центра описанной окружности на серединном перпендикуляре
  

к стороне треугольника;

• 
  следствие из теоремы синусов о радиусе описанной около тре­угольника окружности.
  

• 
  
  

Наиболее часто в заданиях встречались задачи, где требовалось применить первые два свойства. Рассмо­трим примеры таких задач.
Задача 11.Около равнобедренного треугольника ABC с осно­ванием АС и углом при основании 75° описана окружность с центром О. Найдите ее радиус, если площадь треугольни­ка ВОС равна 16.

РЕШЕНИЕ.

	Известно, что вписанные углы, опирающиеся на одну и ту же дугу (или равные дуги), равны между собой и измеряют­ся половиной градусной меры соответствующего центрального угла. В рассматриваемом примере нужно (как промежуточное действие) вычислить центральный угол по соответствующему впи­санному углу. Решение задачи состоит из двух шагов.
1) Используя связь между вели­чинами соответствующих вписанного и центрального углов, имеем: 2) R = 8. Ответ: 8.

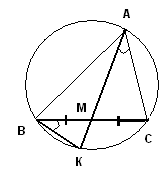
Заметим, что в некоторых задачах используется связь между вписанным углом (углом вписанного треуголь­ника), противолежащей стороной и радиусом описанной окружности (формула - из теоремы синусов) или между цент­ральным углом, противолежащей сто­роной и радиусом описанной окруж­ности (теорема косинусов: ).
Задача 12. Около треугольни­ка ABC описана окружность. Медиа­на треугольника AM продлена до пе­ресечения с окружностью в точке К. Найдите сторону АС, если АМ= 18, МК = 8, ВК = 10.

РЕШЕНИЕ.

	При решении этой задачи ис­пользуются два ключевых момента, связанные с двумя пересекающимися хордами одной окружности. 1) Первый — свойство отрезков хорд: ВМ · МС = AM · МК, откуда ВМ = МС = .
2) Второй — подобие треугольников, которые получаются, если соединить концы этих хорд (у этих треугольников есть две па­ры соответственно равных углов: вертикальные углы АМС и ВМК и вписанные углы МВК и MAC, опирающиеся на одну и ту же дyгy КС).Из подобия треугольников ВМК и АМС следует откуда Ответ: 15.

Необходимо заметить, что свойство отрезков пересекающих­ся хорд - факт, который удобно применять при решении задач, но без него можно обойтись, если использовать подобие тре­угольников. В частности, в рассмотренной выше задаче можно записать пропорциональность всех сторон: и выполнить вычисления, приведенные выше, используя сначала левую пропорцию, а затем правую.
2.3. Задачи с четырехугольниками
Трапеция

Задача 13. Боковая сторона рав­нобедренной трапеции равна , а основания равны 3 и 4. Найдите диагональ трапеции.

РЕШЕНИЕ.

Ответ: 5.

1) 2) 3) BD = 5.

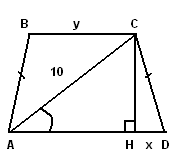
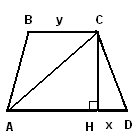
Задача 14. Найдите площадь равнобедренной трапеции, если ее диагональ, равная 10, образует с основанием угол, косинус которого равен .

РЕШЕНИЕ.

	1)Проведем высоту СН. Обозначим ВС= у, НD =x По свойству равнобокой трапеции АD = у + 2х, АН = х + у. 2) BC + AD = 2y + 2x, тогда 3) Из АСН : АН = АС · cos ,
(по теореме Пифагора) 4) = Ответ: 14.

Задача 15. Найдите площадь равнобедренной трапеции, если ее высота равна 3, а тангенс угла между диагональю и основанием равен .

РЕШЕНИЕ.

	Обозначим ВС= у, НD =x. По свойству равнобокой трапеции АD = у + 2х, АН = х + у. 2) BC + AD = 2y + 2x, тогда = AH·CH= 3·AH, 3) Из АСН: CН = AН · tg
3 = AН · ,

AH = 12,

Ответ: 36.
Задача 16. Найдите площадь равнобедренной трапеции, если ее диаго­наль равна а средняя линия равна 4.

РЕШЕНИЕ.

	1) Проведем высоту СН. Обозначим ВС= у, НD =x. По свойству равнобокой трапеции АD = у + 2х, АН = х+у. 2) Средняя линия трапеции равна
3) Из АСН: по теореме Пифагора 4) = 4∙6 = 24. Ответ: 24.

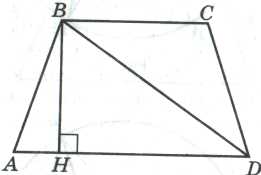
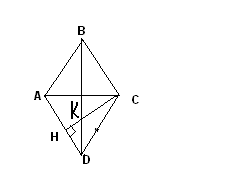
Ромб

Задача 17. Дан ромб ABCD с острым углом В. Площадь ромба 320, а синус угла В равен 0,8. Высота CH пересекает диагональ BD в точке К. Найдите длину отрезка СК.

РЕШЕНИЕ.

	Применение свойств биссектрисы угла треугольника, формул площадей ромба. 1) = АВ∙ВС∙sin В. Пусть АВ=ВС=х, где х>0. х ∙ sin В = 320, x = 320 : 0,8 = 400, x = 20. Сторона ромба равна 20. 2) = АD∙СH, 20∙СH = 320, СH = 16.
3) Из ΔCHD по теореме Пифагора 4) По свойству диагоналей ромба - DК биссектриса СDH. Применим свойство биссектрисы угла треугольника (биссектриса делит противоположную сторону на отрезки пропорциональные прилежащим сторонам) СDH: . Пусть КС = х, тогда HK = 16 – x, 12x = 320 – 20x, 32x = 320, x = 10. КС = 10. Ответ: 10.