6 вариант. Задача 1
 Скачать 4.32 Mb. Скачать 4.32 Mb.
|
|
6 вариант. Задача 1 Смесь газов (2 кг N2 + 8 кг H2) с начальной температурой t1 = 270C сжимается в одноступенчатом поршневом компрессоре от давления Р1 = 0,1 МПа до давления Р2 = 0,9МПа. Сжатие может происходить по изотерме, адиабате и по политропе с показателем политропы n = 1,23. Определить для каждого из трёх процессов сжатия конечную температуру газа t2, отведённое от смеси тепло Q, кВт, изменение внутренней энергии и энтропии смеси и теоретическую мощность компрессора, если его производительность G = 0,8*103 кг/ч. Дать сводную таблицу и изображение процессов сжатия в PV– и TS–диаграммах. Решение: Газовая постоянная смеси RCM = 8314/ µCM, где µCM - молекулярная масса смеси; µCM= 1/[(mN2/ µN2) + (mH2/ µH2)], µN2= 28 кг/кмоль -молекулярная масса азота µH2 = 2 кг/кмоль -молекулярная масса водорода. Массовые доли азота и водорода а в смеси: MN2 = MN2 / Mсм; mH2 = MH2/ Mсм; где MN2 – масса азота; MH2 – масса водорода; Мсм – масса смеси, равная Мсм = MN2 + MH2. Мсм = 2 + 8 = 10 кг. mN2 = 2/10 = 0,2; mH2 = 8/10 = 0,8. µCM= 1/[(0,2/ 28) + (0,7/2)] = 2,8, RCM = 8314/ 2,8 = 2969 Дж/(кг*К). Начальный объём смеси Запишем уравнение состояния Р1*V1 = M*RCM*T1, из которого выразим объём смеси: V1 = M*RCM*T1/P1 = 10*2969*300 / (0,1*106) = 89,07 м3. Массовая изобарная теплоёмкость смеси Cрсм = 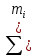 *Cpi), *Cpi),где Cpi = µCрi /µi - массовая изобарная теплоёмкость i-го компонента смеси µCрi = 29,1 кДж/(кмоль*К) – мольная изобарная теплоёмкость азота и водорода(для двухатомных газов), Cрсм = 0,2*29,1/28 + 0,8*29,1/2 = 11,848 кДж,(кг*К). Массовая изохорная теплоёмкость смеси Cvсм = 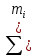 *Cvi), *Cvi),где Cvi = µCvi /µi - массовая изохорная теплоёмкость i-го компонента смеси µvрi = 20,93 кДж/(кмоль*К) – мольная изохорная теплоёмкость азота и водорода(для двухатомных газов), Cvсм = 0,2*20,93/28 + 0,8*20,93/2 = 8,522 кДж,(кг*К). Показатель адиабаты: k = Cрсм/Cvсм = 11,848/8,522 = 1,39. Изотермическое сжатие. Конечное давление по условию задачи Р2 = 0,9 МПа. При изотермическом процессе T2 = T1 = 300 K. Конечный объём определяем по уравнению: V2 = RCM*Т2 / P2 = 2969*300 / (0,9*106) = 0,98 м3. Работа сжатия: L = M* RCM*T*ln(V2/V1) = 10*2969*300*ln(0,98/89,07) = - 40167233 Дж. Изменение внутренней энергии: При изотермическом процессе температура не меняется, поэтому ∆U =0 Количество теплоты, участвующее в процессе: Так как по первому закону термодинамики Q = L + ∆U, и ∆U = 0, то Q = L = - 40167233 Дж. Изменение энтропии: ∆S = M*RCM*ln(V2/V1) = 10*2969*ln(0,98/89,07) = - 133891Дж/К. Изменение энтальпии: При изотермическом процессе ∆Н = 0. Теоретическая мощность компрессора: N = G*n*lсж = (0,8*103/3600)*1*4016723,3 = 892605 Вт. n = 1; lсж = L/M = 40167233/10 = 4016723,3 Дж/кг. Адиабатное сжатие. Конечное давление по условию задачи Р2 = 0,9 МПа. Конечную температуру определяем из уравнения: T2 = T1*(Р2 / Р1 )(k-1)/k = 300*(0,9/0,1)(1,39-1)/1,39 = 556 K. k – показатель адиабаты. Конечный объём определяем по уравнению: V2k = P1*V1k / P2, V21,39 = 0,1*106*89,071,39 / (0,9*106) = 57; V2 = 18,33 м3. Работа сжатия: L = (M* RCM /(k – 1))*(T1 - T2) = (10*2969 / (1,39 – 1))*(300 - 556) = = -19488821Дж. Количество теплоты, участвующее в процессе: Так как процесс адиабатный, то Q = 0. Изменение внутренней энергии: Так как по первому закону термодинамики Q = L + ∆U, и Q = 0, то ∆U = - L = 19488821Дж. Изменение энтропии: При адиабатном процессе ∆S = 0. Изменение энтальпии: ∆Н = М*Срсм*(Т2 – Т1), ∆Н = 10*948*(556 – 300) = 2426880 Дж. Теоретическая мощность компрессора: N = G*n*lсж = (0,8*103/3600)*1,39*1948882,1 = 601988 Вт. n = k = 1,39; lсж = L/M = 19488821/10 = 1948882,1Дж/кг. Политропное сжатие Конечное давление по условию задачи Р2 = 0,9 МПа. Конечную температуру определяем из уравнения: T2 = T1*(P2 / P1 )(n-1)/n = 300*(0,9/0,1)(1,23-1)/1,23= 553 K. Конечный объём определяем из уравнения: V2n = P1*V1n / P2, V21,23= 0,1*106*89,071,23 / (0,9*106) = 27,8; V2 = 14,93 м3. Работа расширения: L =[M* RCM /(n – 1)]*(T1 - T2) = [10*2969 / (1,23 – 1)]*(300 - 553) = = - 32659000Дж. Количество теплоты, участвующее в процессе: Q = [М*Cvсм *(n – k)/(n – 1)]*(T2 – T1), Q = [10*682*(1,23 – 1,39)/(1,23 – 1)]*(553 – 300) = - 1200320 Дж. Изменение внутренней энергии: ∆U = М*Cvсм*(T2 – T1) = 10*682*(553 – 300) = 1725460 Дж. Изменение энтропии: ∆S = M*Cvсм* [(n – k)/(n – 1)]/ ln(T2/T1), ∆S = 10*682*103* [(1,23 – 1,39)/(1,23– 1)]*ln(553/300) = - 2901527 Дж/К. Изменение энтальпии ∆Н = М*Срсм*(Т2 – Т1) = 10*948*(553 – 300) = 2398440 Дж. Теоретическая мощность компрессора: N = G*n*lсж = (0,8*103/3600)*1,23*3265900 = 892679 Вт. n = 1,23; lсж = L/M = 32659000/10 = 3265900 Дж/кг. Результаты расчёта.
Анализируя данные таблицы, приходим к выводу, что в адиабатном процессе теплота не подводится и не отводится. В изотермическом процессе сжатия теплота отводится. Политропный процесс сжатия (имеем 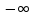 < n < < n < 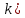 протекает также с отводом теплоты от рабочего тела. Наибольшая работа совершается при изотермическом процессе, так как не меняется температура в процессе, следовательно и внутренняя энергия системы также не меняется, а тепло, подведённое, расходуется на совершение работы этой системой. протекает также с отводом теплоты от рабочего тела. Наибольшая работа совершается при изотермическом процессе, так как не меняется температура в процессе, следовательно и внутренняя энергия системы также не меняется, а тепло, подведённое, расходуется на совершение работы этой системой.Изображение процессов расширения в PV- и TS- диаграммах  Р,МПа V,м3 Р1 Р2 V1 1    2ад 2из 2п  Т,К ∆S,кДж/К   1 2ад 2из 2п 
процесс 1-2из – изотермическое сжатие; процесс 1 -2ад – адиабатное сжатие; процесс 1 – 2п – политропное сжатие В каком из процессов сжатия мощность, затрачиваемая на привод компрессора, будет больше? В политроном процессе сжатия мощность, затрачиваемая на привод компрессора, будет больше, чем при изотермическом и адиабтном сжатии. Какое количество воды необходимо прокачивать через рубашку цилиндра при сжатии газа по изотерме и политропе, если температура воды при этом повышается на 200? Kоличество охлаждающей воды: МН2О = Q/(CH2O*∆t): - при сжатии по изотерме: МН2О = 40167233/(4190*20) = 479 кг. - при сжатии по политропе: МН2О = 1200320/(4190*20) = 143 кг. Как изменится в вашем варианте задачи показатель адиабаты k = Cp/Cv, если учесть зависимость теплоёмкости газов от температуры? Находим теплоёмкость смеси в промежутке температур t1 – t2 (например, при адиабатном процессе t1 = 270C; t2 = 2830C): (СpN2)t1t2 = (Cp2N2*t2 - Cp1N2*t1)/(t2 – t1) = (1,0455*283 – 1,0392*27)/(283 – 27)= 1,046 кДж/(кг*К); (СpH2)t1t2 = (Cp2H2*t2 - Cp1H2*t1)/(t2 – t1) = (14,435*283 – 14,252*27)/(283 – 27) = 14,454 кДж/(кг*К); Срi – изобарная теплоёмкость азота и водорода при t1 и t2 CpCM = mN2*(СpN2)t1t2 + mH2*(СpH2)t1t2 CpCM = 0,2*1,046 + 0,8*14,454 = 11,772 кДж/(кг*К) (СvN2)t1t2 = (Cv2N2*t2 – Cv1N2*t1)/(t2 – t1) = (0,7502*283 – 0,7424*27)/(283 – 27)= 0,908 кДж/(кг*К); (СvH2)t1t2 = (Cv2H2*t2 – Cv1H2*t1)/(t2 – t1) = (10,302*283 – 10,128*27)/(283 – 27) = 10,320 кДж/(кг*К). Сvi – изохорная теплоёмкость азота и водорода при t1 и t2 CvCM = mN2*(СvN2)t1t2 + mH2*(СvH2)t1t2 CvCM = 0,2*0,908 + 0,8*10,320 = 8,438 кДж/(кг*К) k = CpCM/CvCM = 14,454/8,438 = 1,71. Если учесть зависимость теплоёмкости от температуры, то в нашем случае коэффициент адиабаты увеличится. Задача 2. Водяной пар с начальным давлением Р1 = 10МПа и степенью сухости Х1 = 0,95 поступает в пароперегреватель, где его температура повышается на ∆t=2500С, после пароперегревателя пар изоэнтропно расширяется в турбине до давления Р2 = 3,5 кПа. Определить (по h-s – диаграмме) количество теплоты (на 1 кг пара), подведённое в пароперегревателе, работу цикла Ренкина и степень сухости пара Х2 в конце расширения. Определить также термический КПД цикла и удельный расход пара. Определить работу цикла и конечную степень сухости, если после пароперегревателя пар дросселируется до давления Р1* = 2,5 МПа. Изобразить схему паротурбинной установки и цикл Ренкина в p–V- и T–s- диаграммах. Решение: Задачу решаем при помощи hS- диаграммы. Начальное состояние – точка 0 – на пересечении изобары Р1 = 10 МПа и линии постоянной сухости Х1 = 0,95. В этой точке энтальпия h0 = 2670 кДж/кг, температура t0 = 3000С. Состояние пара после пароперегревателя – точка 1 – на пересечении линии изобары Р1 = 10 МПа и изотермы t = t0 + ∆t = 300+250 = 5500С. В этой точке энтальпия h1 = 3500 кДж/кг. Конечное состояние пара – точка 2 – на пересечении изобары Р2 = 3,5 кПа и линии постоянной энтропии. В этой точке энтальпия h2 =2030 кДж/кг, степень сухости Х2 = 0,785 . По таблицам для насыщенного водяного пара определяем при Р2 = 3,5 кПа h21 =111,86 кДж/кг[1]. Количество теплоты, подведённое к пару в пароперегревателе: q = h1 – h0 = 3500 – 2670 = 830 кДж/кг. Работа цикла Ренкина: l0 = h1 – h2 = 3500 – 2030 = 1470 кДж/кг. Удельный расход пара: d0 = 3600/( h1 – h2) = 3600/(3500 – 2030) = 2,45кг/(кВт*ч). Термический КПД цикла ηt = (h1 – h2)/(h1 – h21 ) = (3500 – 2030)/(3500 – 111,86) = 0,434. Пар после пароперегревателя дросселируется до давления Р1* = 2,5 МПа. Промежуточное состояние пара – точка 2а – на пересечении линии постоянной энтальпии h1 = 3500 кДж/кг и изобары Р1* = 2,5 МПа. Конечное состояние пара – точка 2 – на пересечении изобары Р2 = 3,5 кПа и линии постоянной энтропии. В этой точке энтальпия h2 =2210 кДж/кг, степень сухости Х2 = 0,86 . По таблицам для насыщенного водяного пара определяем при Р2 = 3,5 кПа h21 =111,86 кДж/кг[1]. Количество теплоты, подведённое к пару в пароперегревателе: q = h1 – h0 = 3500 – 2670 = 830 кДж/кг. Работа цикла Ренкина: l0 = h2а – h2 = 3500 – 2210 = 1290 кДж/кг. Удельный расход пара: d0 = 3600/( h1 – h2) = 3600/(3500 – 2210) = 2,79кг/(кВт*ч). Термический КПД цикла ηt = (h2а – h2)/(h1 – h21 ) = (3500 – 2210)/(3500 – 111,86) = 0,381. 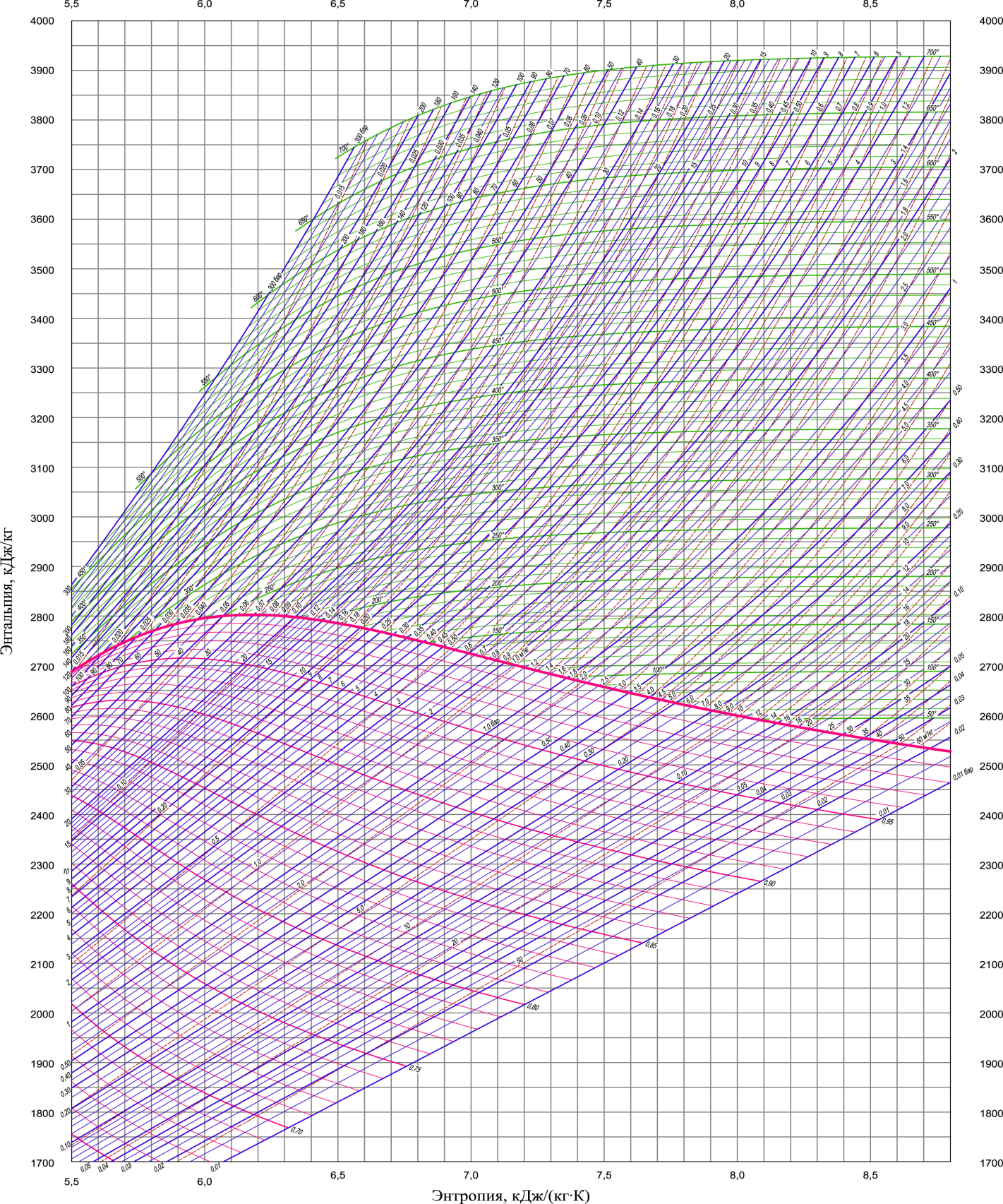    0 t1 h0 t0  s1 1  X1 h1  s2 P2   h2 2a     P2’    2  X2     X2’ h2’ Схема паротурбинной установки  котёл; 2- пароперегреватель; 3- паровая турбина; 4 – конденсатор; 5- генератор; 6- насос. Цикл Ренкина в p–V- и T–s- диаграммах.  Как влияют начальная температура и давление перегретого пара, а также процесс дросселирования на величину конечной степени сухости пара х2? С повышением начального давления в паровом котле от р1"′ до р1′ при постоянной температуре перегрева t1 и при постоянном давлении р2 в конденсаторе уменьшается степень сухости пара на выходе из турбины. 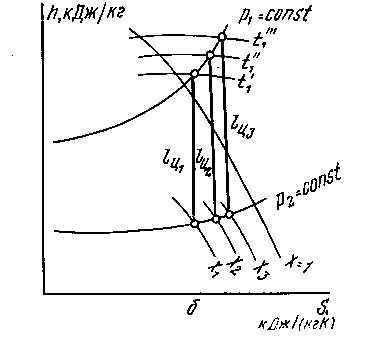 При повышении температуры перегрева пара от t1′ до t1′" (при постоянных начальном р1 и конечном р2 давлениях) увеличивается конечная степень сухости пара (х2) При повышении температуры перегрева пара от t1′ до t1′" (при постоянных начальном р1 и конечном р2 давлениях) увеличивается конечная степень сухости пара (х2)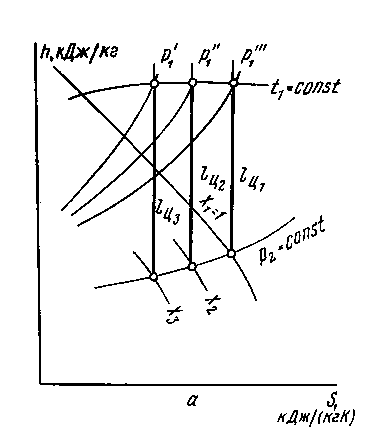 Влияние давления (a) и температуры (б) пара на к.п.д. цикла Ренкина. При дросселировании пара конечная степень сухости возрастает, что хорошо видно из h-S–диаграммы. 1-2 – процесс расширения пара без дросселирования; 1-2а-3 – процесс расширения пара с промежуточным дросселированием.   2a h P1 Pдр  1  P2      3      2 S   X2* X2 Какое следует выбрать давление промежуточного перегрева в вашем варианте задачи, чтобы в конце расширения пар имел степень сухости х2=0,95? (в этом случае температуру промежуточного перегрева следует принять на 30оС меньше начальной температуры t1).  h P1 1 t1 Pпер      tпер     t0 0  P2  2a a     2 X=1 X2=Х1= 0,95 S  Находим точку 2 – на пересечение линии Х2 = 0,95 и изобары Р2 = 3,5кПа. Из полученной точки проводим адиабату до пересечения с изотермой tпер = t1 – 30 = 550 – 30 = 5200С – точка 2а. Изобара, проходящая через полученную точку – давление промежуточного перегрева Рпер = 0,48 МПа. 3. Как влияет промежуточный перегрев на конечную сухость пара? Конечная степень сухости пара повышается с введением промежуточного перегрева. Это хорошо видно из h-S - диаграммы, характеризующей процесс с промежуточным перегревом пара (Х2*).    Х2 Х2*   Задача 3. По горизонтально расположенной стальной трубе (λ = 20 Вт/(м*К)) со скоростью W1 = 2,1 м/с течёт вода, имеющая температуру tB = 1700С. Снаружи труба охлаждается воздухом, температура которого tвозд = 180С, a давление 0,1 МПа. Определить: коэффициенты теплоотдачи α1 и α2 соответственно от воды к стенке трубы и от стенки трубы к воздуху; коэффициент теплопередачи k и тепловой поток ql, отнесённый к 1 м длины трубы, если внутренний диаметр трубы равен d1 = 190 мм, внешний – d2 = 210 мм. Решение: Определяем коэффициент теплоотдачи от воды к стенке трубы. При tB = 1700С определяем параметры воды[2] : - коэффициент теплопроводности λж1 = 0,679 Вт/(м*К); - коэффициент кинематической вязкости νж1 = 0,181*10-6 м2/с; - число Прандтля Prж1 = 1,05. Число Рейнольдса: Reж1d1 = W1*d1 / ν1 = 2,1*0,19/(0,181*10-6) =2,20*106. Так как Re ж1d1 = 2,20*106 > 104, режим движения воды – турбулентный, критериальное уравнение для определения числа Нуссельта (горизонтальная труба) имеет вид[1]: Nuж1d1 = 0,021*Reж1d10,8*Prж1 0,43 = 0,021*(2,20*106)0,6*1,050,43 = 137. Коэффициент теплоотдачи: α1 = Nu ж1d1*λж1/d1 = 137*0,679/0,19 = 489,6 Вт/(м2*К). Определяем коэффициент теплоотдачи от стенки трубы к воздуху При tвозд = 180С определяем параметры воздуха[1]: - коэффициент теплопроводности λж2 = 0,0253 Вт/(м*К); - коэффициент кинематической вязкости νж2 = 14,18*10-6 м2/с; - число Прандтля Prж2 = 0,704. Определяем число Грасгофа: Grж2d2 = g*d2 3*β*∆t/ν2 2, ∆t = tв – tвозд = 170 – 18 = 1520C, β = 0,003436 K-1. Grж2d2 = 9,81*0,213*0,003436*152/(14,18*10-6)2 = 2,36*108. Для горизонтальной трубы критериальное уравнение для определения числа Нуссельта имеет вид[2]: Nu ж2d2= 0,05*(Grж2d2*Prж2)0,25 = 0,05*(2,36*108*0,704)0,25 = 57. Получаем α2 = Nuж2d2*λж2 / d2 = 57*0,0253/0,21 = 6,87 Вт/(м2*К).. Линейный коэффициент теплопередачи от воды к воздуху через цилиндрическую стенку: k =1/ [1/(d1*α1)+ (1 / 2λ)*ln(d2/d1) +1/(α2*d2)), где d1 – внутренний диаметр трубы; d2 – наружный диаметр трубы; λ – коэффициент теплопроводности материала трубы, λ = 20 Вт/(м*К). k =1/ [1/(0,19*489,6)+ (1 / 2*20)*ln(0,21/0,19) +1/(6,87*0,21)) = 1,42 Вт/(м*К). Тепловой поток, отнесённый к 1 м трубы: ql = k*π*( tв – tвозд) = 1,42 * 3,14*(170 –18) = 677,74 Вт/м. Ответы на вопросы: Какой режим течения внутри трубы в вашем варианте задачи? Режим течения воды внутри трубы – турбулентный. Какой режим движения окружающего трубу воздуха? Режим движения окружающего трубу воздуха – свободный конвективный. Почему можно при расчёте принять равенство температур наружной поверхности трубы и воды? Так как стенка трубы имеет небольшую толщину и высокий коэффициент теплопроводности, можно при расчёте принять равенство температур наружной поверхности трубы и воды. Литература. Рабинович О.М. Сборник задач по технической термодинамике. – М.:Машиностроение,1973. – 344 с. 2.Нащокин В.В. Техническая термодинамика и теплопередача. Учебное пособие для вузов. – М.: Высшая школа, 1980. |
