Контрольная по термодинамике. вариант 01. Задание 1 Расчет параметров и процессов смеси идеальных газов
 Скачать 0.75 Mb.
|
|
Задание № 1 Расчет параметров и процессов смеси идеальных газов Смесь газов с начальной температурой Т1 = 300 К сжимается от давления p1 = 0,1 МПа до давления p2. Сжатие может происходить по изотерме, по адиабате и по политропе с показателем политропы n. Определить для каждого из трех процессов сжатия конечную температуру Т2 и объем V2 смеси, изменение внутренней энергии U, энтальпии H и энтропии смеси ΔS, а также теплоту Q и работу L. Результаты расчетов занести в таблицу 2 и изобразить процессы сжатия в p-v и T-S – диаграммах. Данные, необходимые для решения задачи, выбрать из таблицы 1. Примечание. Расчет провести, приняв теплоемкость постоянной.
Определим параметры газовой смеси, состав которой задан массовым способом. Выпишем молярные массы компонентов смеси: углекислый газ (СО2)  ,угарный газ (СО)  .Масса газовой смеси  .Массовые доли компонентов смеси вычислим по формуле  , , .. Газовую постоянную смеси газов определим по формуле  , (1)где  – газовая постоянная i-го компонента смеси.Учитывая, что  , где  – молекулярная масса i-го компонента смеси, выражение (1) примет вид .Кажущуюся молекулярную массу смеси вычислим по формуле  .По условию задачи теплоемкости компонентов смеси не зависят от температуры. По таблице 3 [4, с. 38] находим мольную изобарную теплоемкость трехатомного газа СО2  и двухатомного газа СO  .Вычислим массовые изобарные теплоемкости газовой смеси  , .Вычислим массовую изобарную теплоемкость газовой смеси  кДж/(кг ∙ К) == 951,6 Дж/(кг ∙ К). Из уравнения Майера найдем массовую изохорную теплоемкость газовой смеси  .Показатель адиабаты газовой смеси  .Объем газовой смеси в начальном состоянии (точка 1 на рис. 1 и 2) определим из уравнения состояния  ,откуда  .1. Рассмотрим изотермический процесс сжатия. Так как Т = const, то Т1 = Т2 = 300 К. Уравнение связи давления и объема газовой смеси в изотермическом процессе имеет вид  ,откуда объем газовой смеси в конечном состоянии  м3.Так как в изотермическом процессе Т = const, то изменение внутренней энергии и энтальпии равно нулю, т.е.  и  .Изменение энтропии в изотермическом процессе определим по формуле  .Работу изменения объема в изотермическом процессе определим по формуле  Внешняя работа в изотермическом процессе  .Знак «–» означает, что внешняя работа затрачивается на сжатие газа. Согласно первому началу термодинамики, количество теплоты  .2) Рассмотрим адиабатный процесс сжатия. Уравнение связи температуры и давления в адиабатном процессе имеет вид 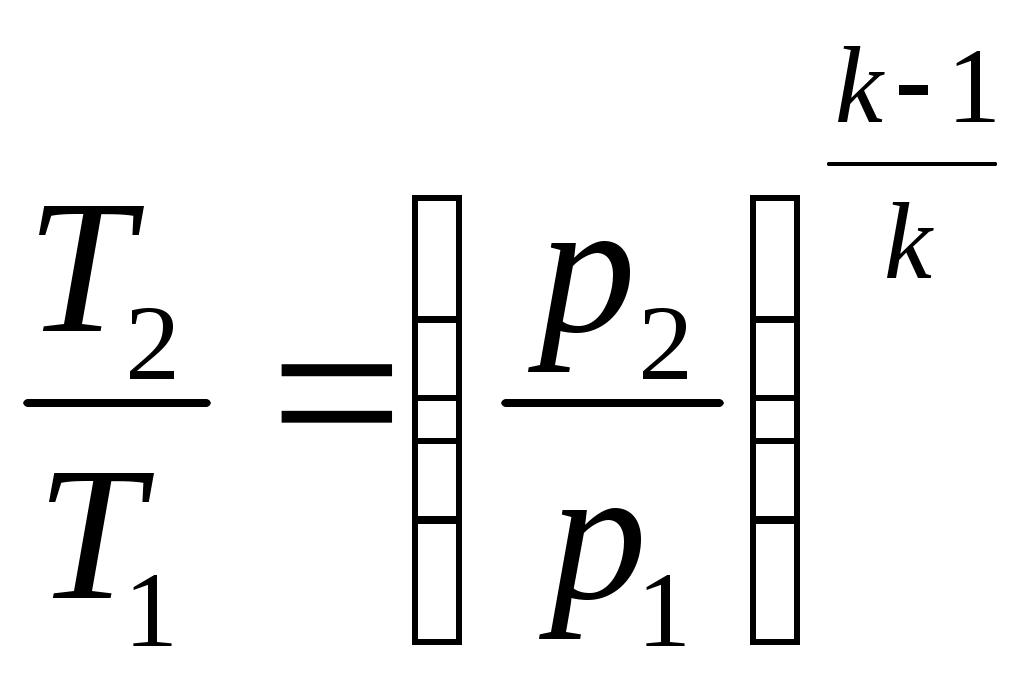 ,откуда температура газовой смеси в конечном состоянии  .Уравнение связи давления и объема в адиабатном процессе имеет вид  ,откуда объем газовой смеси в конечном состоянии  м3.Изменение внутренней энергии  .Изменение внутренней энтальпии  .Так как адиабатный процесс протекает без теплообмена с окружающей средой, то количество теплоты в адиабатном процессе Q = 0, изменение энтропии  .Согласно первому началу термодинамики, количество теплоты  ,откуда работа изменения объема в адиабатном процессе  .Внешняя работа  .Знак «–» означает, что внешняя работа затрачивается на сжатие газа. 3) Рассмотрим политропный процесс сжатия. Уравнение связи температуры и давления в политропном процессе имеет вид  ,откуда температура газовой смеси в конечном состоянии  .Уравнение связи давления и объема в политропном процессе имеет вид  ,откуда объем газовой смеси в конечном состоянии  м3.Изменение внутренней энергии  .Изменение внутренней энтальпии  .Работа изменения объема в политропном процессе  .Внешняя работа  кДж.Удельная теплоемкость политропного процесса   .Изменение энтропии в политропном процессе  Согласно первому началу термодинамики, количество теплоты  .Результаты расчетов сведем в таблицу 1. Таблица 1
Изображение процессов в pV-и Ts- диаграммах приведено на рис. 1 и 2.  Рис. 1. Изображение процессов сжатия в pV-диаграмме (1 < n < k)  Рис. 2. Изображение процессов сжатия в Ts- диаграмме (1 < n < k) Выводы: 1. Как следует из рис. 1 и результатов расчета, внешняя работа (т.е. работа затрачиваемая на привод компрессора, используемого для сжатия газовой смеси) при одних и тех же начальных параметрах газовой смеси и степени повышения давления p2/p1 будет минимальна в изотермическом процессе (n = 1). C ростом показателя политропы внешняя работа увеличивается. 2. Конечная температура и конечный объем газа увеличиваются с ростом показателя политропы n. 3. В процессе сжатия газовой смеси работа затрачивается. В политропном процессе сжатия (1 < n < k), несмотря на отвод тепла, температура газовой смеси возрастает. Ответ: результаты вычислений сведены в табл. 1. Задание №2. Расчет компрессора. Компрессор, производительностью V1, м3/час, состоящий из m ступеней, сжимает газ от давления р1 до давления р2. Сжатие в ступенях происходит по политропе с показателем n. Промежуточное давление выбрано оптимально, а охлаждение во всех теплообменниках производится до начальной температурыТ1, К. Охлаждающая вода, прокачивающаяся через рубашки цилиндров и теплообменники, нагревается на Δt = 13 °C. Исходные данные для решения задачи приведены в таблице 4. Найти общую мощность, затрачиваемую на сжатие в компрессоре, и расход охлаждающей воды. Сравнить найденную мощность с мощностью, которая затрачивается на сжатие в одноступенчатом компрессоре с процессом с процессом сжатия по политропе с тем же показателем n. Теплоемкость в расчетах считать постоянной. Перед расчетом изобразить принципиальную схему компрессора, а так же процессы сжатия в р-v и Т-s – диаграммах.
Принципиальная схема двухступенчатого компрессора и процессы сжатия вpv- и Ts-диаграммах приведен на рис. 1 и 2. Степень повышения давления в каждой ступени компрессоре будет  .Давление газа после первой ступени   Рис. 1. Принципиальная схема двухступенчатого компрессора 1 и 2– первая и вторая ступени компрессора, 3 – промежуточный охладитель. Стрелками на схеме показано направление движения охлаждающей воды.  Рис. 2. Процессы сжатия воздуха в двухступенчатом компрессоре вpv- и Ts-диаграммах Обозначения: p1,  , р2 – начальное, промежуточное после первой ступени и конечное давления, соответственно, Т1, Т2 – температуры начала и конца сжатия, соответственно; 1–2 и 3–4, – политропное сжатие в первой и второй ступенях компрессора; 2–3– изобарное охлаждение газа в промежуточном холодильнике.Мощность, затрачиваемая на сжатие газа в одной ступени компрессора,  где  – объемный расход газа на входе в компрессор, м3/с.Тогда мощность привода двухступенчатого компрессора  .Теоретическую мощность одноступенчатого компрессора при политропном процессе сжатия определим по формуле 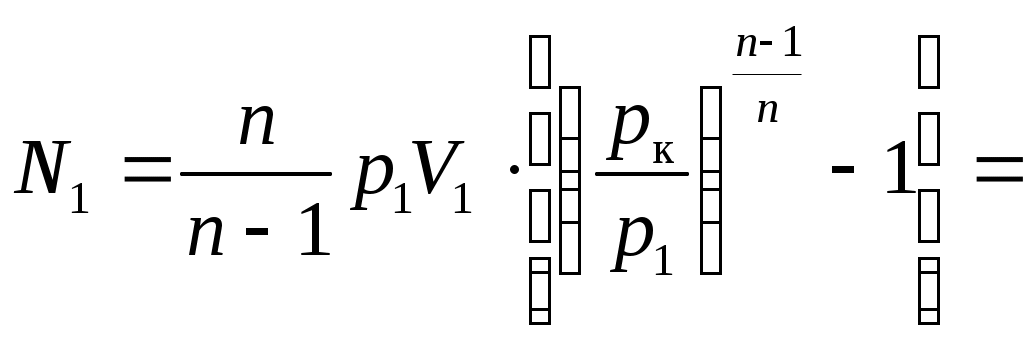  Мощность, затрачиваемая на сжатие газа в одноступенчатом компрессоре, больше мощности, затрачиваемой в двухступенчатом компрессоре, в  раза.Таким образом, сжатие в двухступенчатом компрессоре позволяет сократить затраты энергии по сравнению со сжатием в одноступенчатом компрессоре. В многоступенчатом компрессоре теплота отводится в цилиндрах и в промежуточных теплообменниках-холодильниках. Общий расход отведенной теплоты определяется равенством:  ,где  – тепловой поток, отводимый в систему охлаждения цилиндров в одной ступени компрессора при политропном процессе сжатия воздуха,  – тепловой поток, отводимый от воздуха при охлаждении его от температуры Т2 до температуры Т1 в одном промежуточном теплообменнике.Определим газовую постоянную воздуха  ,где  – универсальная газовая постоянная. Из уравнения состояния определим массовый расход сжимаемого газа  .Температура воздуха после каждой ступени компрессора:  .Так как воздух можно считать двухатомным газом, то его показатель адиабаты k= 1,4 . По таблице 3 [4, с. 38] находим мольную теплоемкость двухатомного газа при постоянном давлении  .Вычислим массовую теплоемкость  воздуха при постоянном давлении  .Используя уравнение Майера, вычислим массовую теплоемкость  воздуха при постоянном объеме .Массовая теплоемкость политропного процесса  .Тепловой поток, отводимый в систему охлаждения цилиндров в одной ступени компрессора  .Охлаждение воздуха в промежуточных охладителях происходит при постоянном давлении, следовательно, тепловой поток, отводимый от воздуха при охлаждении его от температуры Т2 до температуры Т1 в одном промежуточном охладителе, можно определить по формуле  .Определим суммарный тепловой поток, отводимый в систему охлаждения 3 цилиндров и в 2-ех промежуточных охладителях  .Расход охлаждающей воды  через компрессор определим из формулы ,откуда  ,где  = 4,19 кДж/(кг∙К) – теплоемкость воды, Δtв – изменении температуры воды.Выводы: Мощность, затрачиваемая на сжатие газа в одноступенчатом компрессоре, больше мощности, затрачиваемой в двухступенчатом компрессоре, в раза.Таким образом, сжатие в двухступенчатом компрессоре позволяет сократить затраты энергии по сравнению со сжатием в одноступенчатом компрессоре. Ответ:  ;  ;  , . |
(СО2)
(СO)
; 
; 
;
= ?