Контрольная по термодинамике. вариант 01. Задание 1 Расчет параметров и процессов смеси идеальных газов

• Название: Задание 1 Расчет параметров и процессов смеси идеальных газов
• Анкор: Контрольная по термодинамике
• Дата: 17.12.2021
• Размер: 0.75 Mb.
• Имя файла: вариант 01.doc
• Тип: Документы; #307231
• страница: 2 из 3

Задание 3.

Расчет цикла двигателя внутреннего сгорания.

Цикл поршневого двигателя внутреннего сгорания имеет следующие характеристики: n₁ – показатель политропы в процессе сжатия рабочего тела, (процесс 1–2); n₂ – показатель политропы в процессе расширения рабочего тела, (процесс 3–4); – степень сжатия; – степень повышения давления; – степень предварительного расширения. Начальные параметры р₁ и t₁. Принимая за рабочее тело воздух, требуется:

1. Определить тип цикла ДВС;

2. Определить параметры p, v, T для основных точек (1, 2, 3, 4) цикла;

3. Найти теплоту q и работу w для каждого процесса, из которых состоит цикл;

4. Найти работу цикла l₀, термический КПД ηt и среднеиндикаторное давление;

5. Изобразить цикл в Т-s – диаграмме;

6. Показать на р-v и T-s- диаграммах процессы, в которых осуществляется подвод тепла и в которых тепло отводится.

Теплоемкость рабочего тела, обладающего свойствами воздуха принять постоянной (приложение, таблица 1).

Исходные данные, необходимые для решения задачи, приведены в таблице 5 по вариантам индивидуальных заданий.

Результаты расчетов поместить в таблице 6.

Дано: n1 = 1,34 n2 = 1,3

Найти: ; ; ; ; ; ; ;

Решение:

По условию задачи задан цикл двигателя внутреннего сгорания с изохорным подводом тепла.

Изображение цикла ДВС с изохорным подводом тепла в р-v- и T-s –диаграммах приведено на рис. 1.

Определим физические свойства воздуха.

Молярная масса воздуха



Газовая постоянная воздуха

,

где – универсальная газовая постоянная.

Так как воздух можно считать двухатомным газом, то показатель адиабаты для воздуха .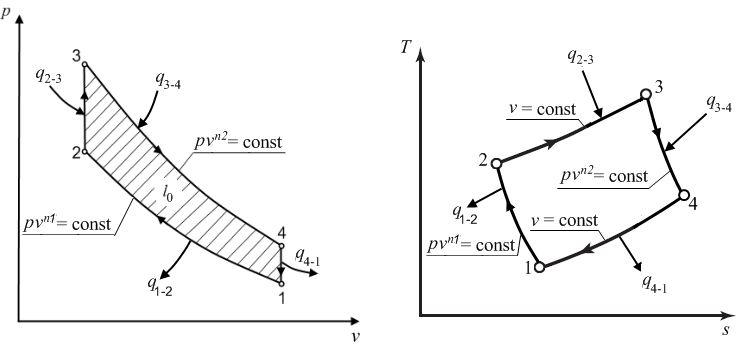



Рис. 1. Цикл ДВС с подводом теплоты при

Обозначения:1–2 – политропное сжатие воздуха в цилиндре (n₁ = 1,34),

2–3 – сгорание топлива (подвод теплоты к рабочему телу) при ,

3–4 – политропное расширение продуктов сгорания в цилиндре (n₂ = 1,3),

4–1 – выхлоп продуктов сгорания (отвод теплоты от рабочего тела) при .
Определим массовую теплоемкость воздуха при постоянном объеме

.

Определим параметры p, v, T для основных точек (1, 2, 3, 4) цикла.

Точка 1.

Давление .

Температура .

Удельный объем в точке 1 определим из уравнения состояния идеального газа

/кг.

Точка 2.

Так как степень сжатия

,

то удельный объем в точке 2

м³/кг.

Давление и удельный объем в политропном процессе 1–2 (с показателем политропы n₁ = 1,34) связаны соотношением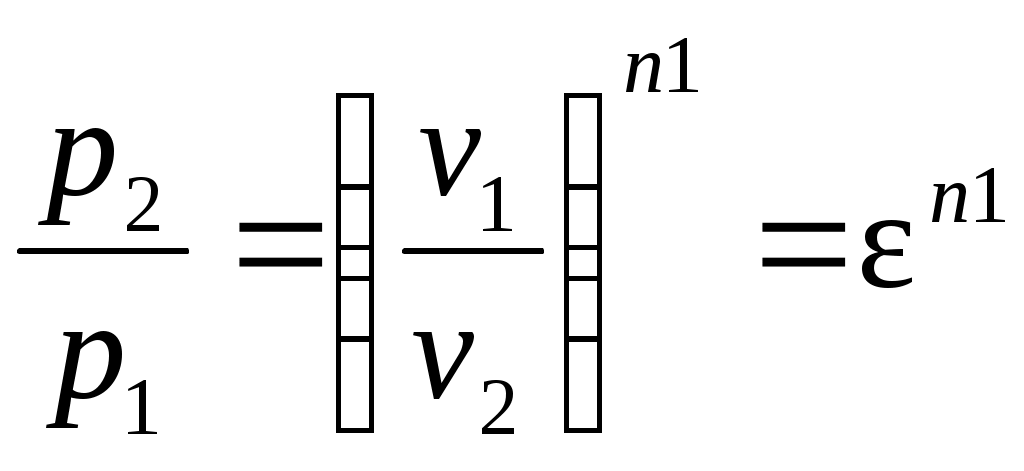

,

откуда давление в точке 2

Па = 0,9819 МПа.

Уравнение связи между температурой удельным объемом в политропном процессе 1–2 (с показателем политропы n₁ = 1,34) имеет вид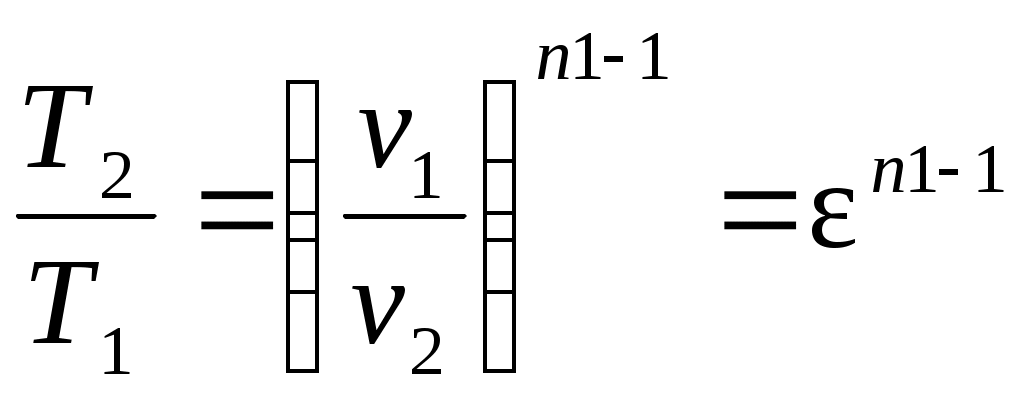

,

откуда температура в точке 2

.

Точка 3.

Так как процесс 2–3 – изохорный, то удельный объем в точке 3

.

Так как степень повышения давления

,

то давление в точке 3

.

Уравнение связи между давлением и температурой в изохорном процессе 2–3

имеет вид

,

откуда температура в точке 3

.

Точка 4.

Так как процесс 4–1 – изохорный, то удельный объем в точке 4

.

Уравнение связи между температурой и удельным объемом в политропном процессе 3–4 (с показателем политропы n₂ = 1,3) имеет вид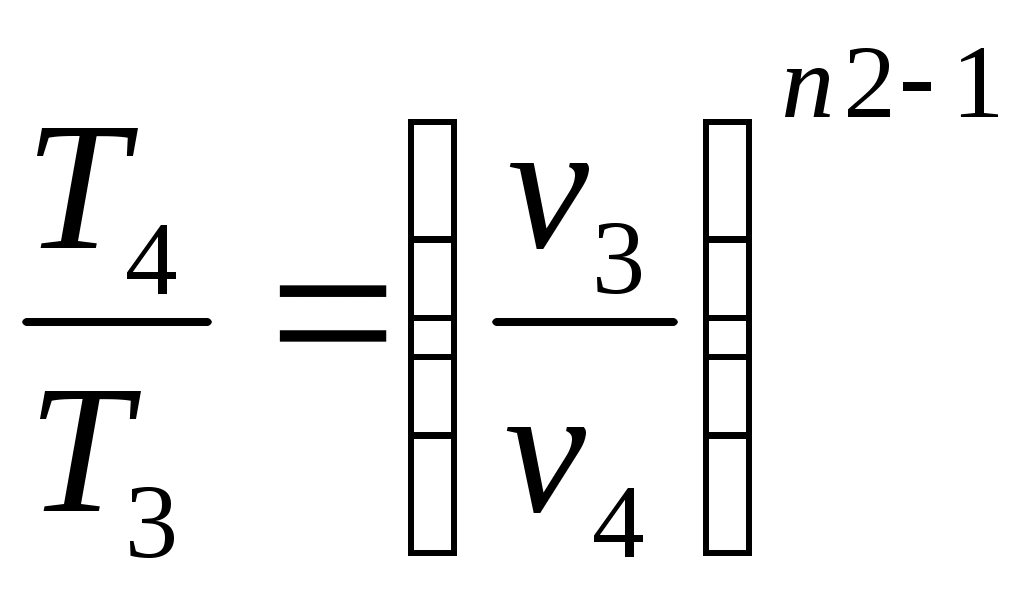

,

откуда температура в точке 4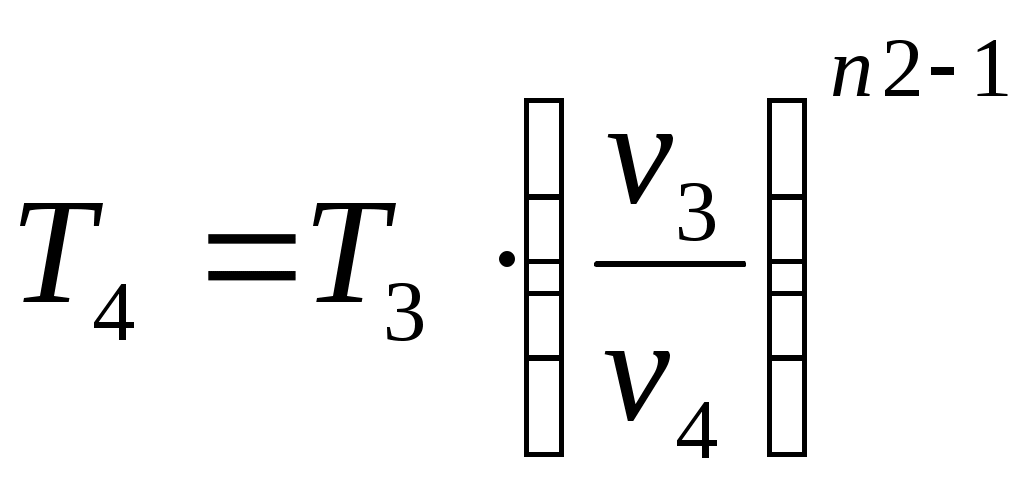

.

Уравнение связи между давлением и температурой в изохорном процессе 4–1 имеет вид

,

откуда давление в точке 4

,

.

Определим теплоту и работу для каждого процесса цикла.

Процесс 1–2 – политропный с показателем политропы n₁ = 1,34.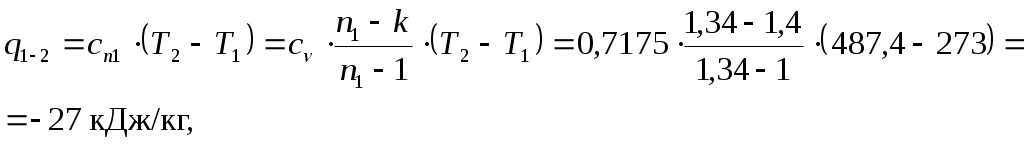



где – теплоемкость политропного процесса 1-2;



Процесс 2–3 – изохорный.

;

.

Процесс 3–4 – политропный с показателем политропы n₂ =1,3.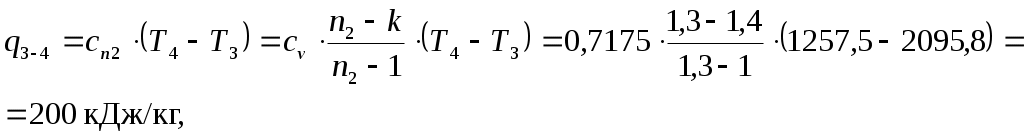



где 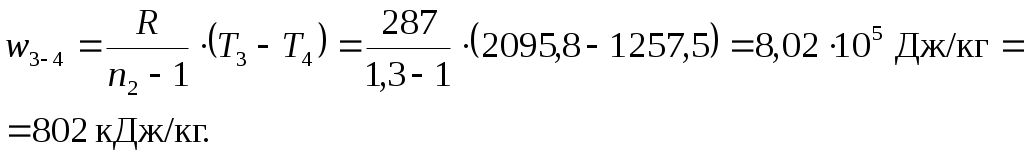– теплоемкость политропного процесса 3–4.



Процесс 4–1 – изохорный.

;

.

Работу цикла определим по формуле

.

Выполним проверку, определив работу цикла по формуле,

,

– верно.

Количество тепла, подведенного за цикл,

кДж/кг.

Термический КПД цикла

.

Среднеиндикаторное давление


Результаты расчетов занесем в таблицу 1.
Таблица 1

Параметры основных точек				Процесс	q, кДж/кг	w, кДж/кг
Точка	Т, К	p, МПа	v, м3/кг	1–2	-27	-181
1	273	0,10	0,78351	2–3	1154	0
2	487,4	0,9819	0,14246	3–4	200	802
3	2095,8	4,222	0,14246	4–1	-706	0
4	1257,5	0,4606	0,78351	∑	621	621

Выводы: рассмотренный цикл является циклом ДВС с подводом теплоты (при сгорании топлива) при постоянном объеме.

Работа цикла . Термический КПД цикла . Среднеиндикаторное давление .
Ответ: результаты расчетов представлены в таблице 1.


Задание № 4

Расчет процесса переноса тепла конвекцией и теплопроводностью

В резервуаре диаметром d и высотой h хранится нефть при температуре t_ж1, снаружи резервуар омывается воздухом с температурой t_ж2. Резервуар выполнен из стали толщиной стен _с = 25мм, коэффициент теплопроводности стали λ_с = 45,4 Вт/(м · К). Со стороны нефти на стенке и на крышке резервуара имеется слой парафина толщиной _п, коэффициент теплопроводности парафина λ_п = 0,12 Вт/(м · К).

Определить количество теплоты, которое передается от нефти к воздуху за сутки через боковую поверхность и крышку резервуара, и температуры наружной и внутренней поверхностей резервуара, а также на поверхности парафина.

Построить график изменения температуры, в стенке резервуара и в слое парафина.

Данные, необходимые для решения, выбрать из таблицы 7.

Дано: с = 25мм = 0,025 м λс = 45,4 Вт/(м · К) λп = 0,12 Вт/(м · К) α1 = 1000 Вт/(м2 · К) α2 = 30 Вт/(м2 · К)

Найти: , = ?

Решение:

Определим внутренний диаметр слоя парафина

.

Определим наружный диаметр резервуара

.

Так как отношение диаметров слоев

,

,

то кривизной слоев стенки можно пренебречь, и цилиндрическую двухслойную стенку можно рассматривать как плоскую двухслойную стенку.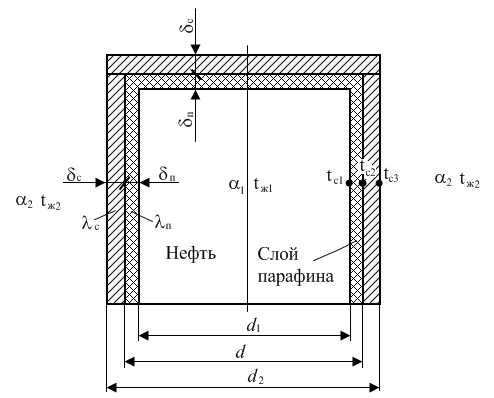



Рис. 1. Схема решения задачи
При этом, так как , то количество теплоты, передаваемой от нефти к воздуху через боковую (цилиндрическую поверхность) резервуара за время , следует определять по формуле [3, c. 204–205]

,

где – плотность теплового потока, – площадь наружной поверхности резервуара.

Определим коэффициент теплопередачи по формуле для плоской двухслойной стенки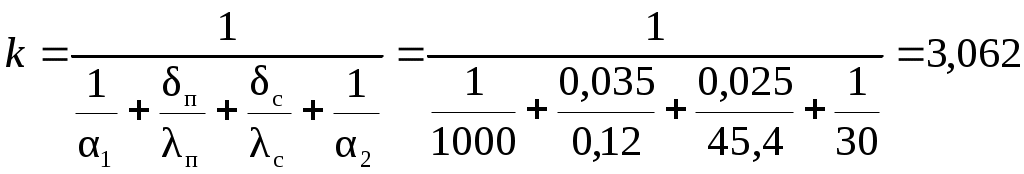

Вт/(м² · К).

Определим плотность теплового потока

Вт/м².

Определим количество теплоты, передаваемой от нефти к воздуху через боковую (цилиндрическую поверхность) резервуара за время ,



Количество теплоты, передаваемой от нефти к воздуху через крышку резервуара за время ,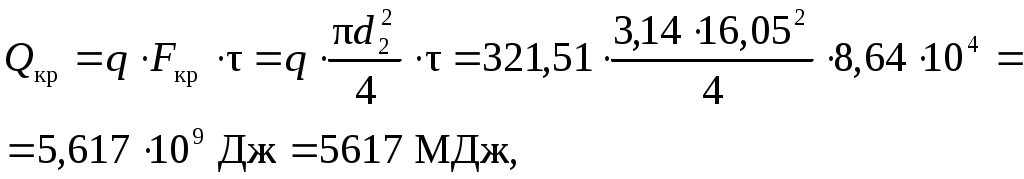



где – площадь поверхности крышки.

Суммарные потери тепла

.

Из уравнения теплоотдачи

,

определим температуру на поверхности парафина

.

Из уравнения теплопроводности

,

определим температуру на поверхности контакта парафина и стенки резервуара

.

Из уравнения теплоотдачи

,

определим температуру на наружной поверхности резервуара

.

График изменения температуры, в стенке резервуара и в слое парафина приведен на рис. 2. Так как кривизной слоев стенки можно пренебречь, то распределение температуры внутри слоев будет линейным.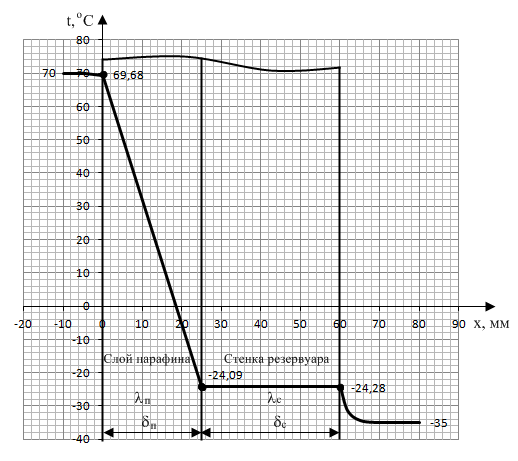


Рис. 2. График изменения температуры по толщине слоев
Выводы:

Как видно из рис. 2, наибольший температурный перепад происходит в слое парафина, так как термическое сопротивление слоя парафина R_п =  является наибольшим.
Ответ: , , , , .